Test del Chi-quadro per conformità
Esercizio 1
L’Associazione Bar dell’Emilia Romagna ha condotto un’indagine sulle preferenze delle bevande dei clienti dei bar della regione. Durante una settimana, sono stati intervistati 250 clienti di vari bar della zona. L’associazione è interessata a capire se le preferenze dei clienti per le bevande differiscono dalla media nazionale.
Qui di seguito è riportata la tabella delle preferenze dei clienti dei bar dell’Emilia Romagna:
| Caffè | Tè | Altro | Totale | |
|---|---|---|---|---|
| Dati Associazione | \(100\) | \(88\) | \(62\) | \(250\) |
| Media Nazionale | \(50\%\) | \(30\%\) | \(20\%\) | \(100\%\) |
Testare l’ipotesi che le preferenze dei clienti dei bar dell’Emilia Romagna per le bevande differiscano dalla media nazionale.
Test \(\chi^2\) per conformità
\(\fbox{A}\) Formulazione delle ipotesi \[ \{H_0:\pi_\text{ Dati Associazione }= \pi_\text{ Media Nazionale },~~\forall j \] \(\fbox{B}\) Scelta e calcolo della statistica test.
Si tratta di un test chi quadro di conformità. \[ n^*_j = n\cdot \pi^*_{\text{ Media Nazionale },j} \]
La tabella delle distanze:
| Caffè | Tè | Altro | Tot | |
|---|---|---|---|---|
| Dati Associazione | 100.0 | 88.000 | 62.00 | 250.00 |
| Media Nazionale | 0.5 | 0.300 | 0.20 | 1.00 |
| \(n_j^*\) | 125.0 | 75.000 | 50.00 | 250.00 |
| \(\chi^2\) | 5.0 | 2.253 | 2.88 | 10.13 |
\[ \chi^2_{obs}= 10.13 \]
i \(gdl\)
\[ ( 3 -1)= 2 \]
\(\fbox{C}\) CONCLUSIONE
I valori critici sono
\(\chi^2_{2;0.1}=4.61\); \(\chi^2_{2;0.05}=5.99\); \(\chi^2_{2;0.01}=9.21\); \(\chi^2_{2;0.001}=13.82\)
Siccome \(9.21<\chi^2_\text{obs}=10.1333<13.82\), quindi rifiuto \(H_0\) all’1%, \(0.001<p_\text{value}<0.01\),
molto significativo \(\fbox{**}\).
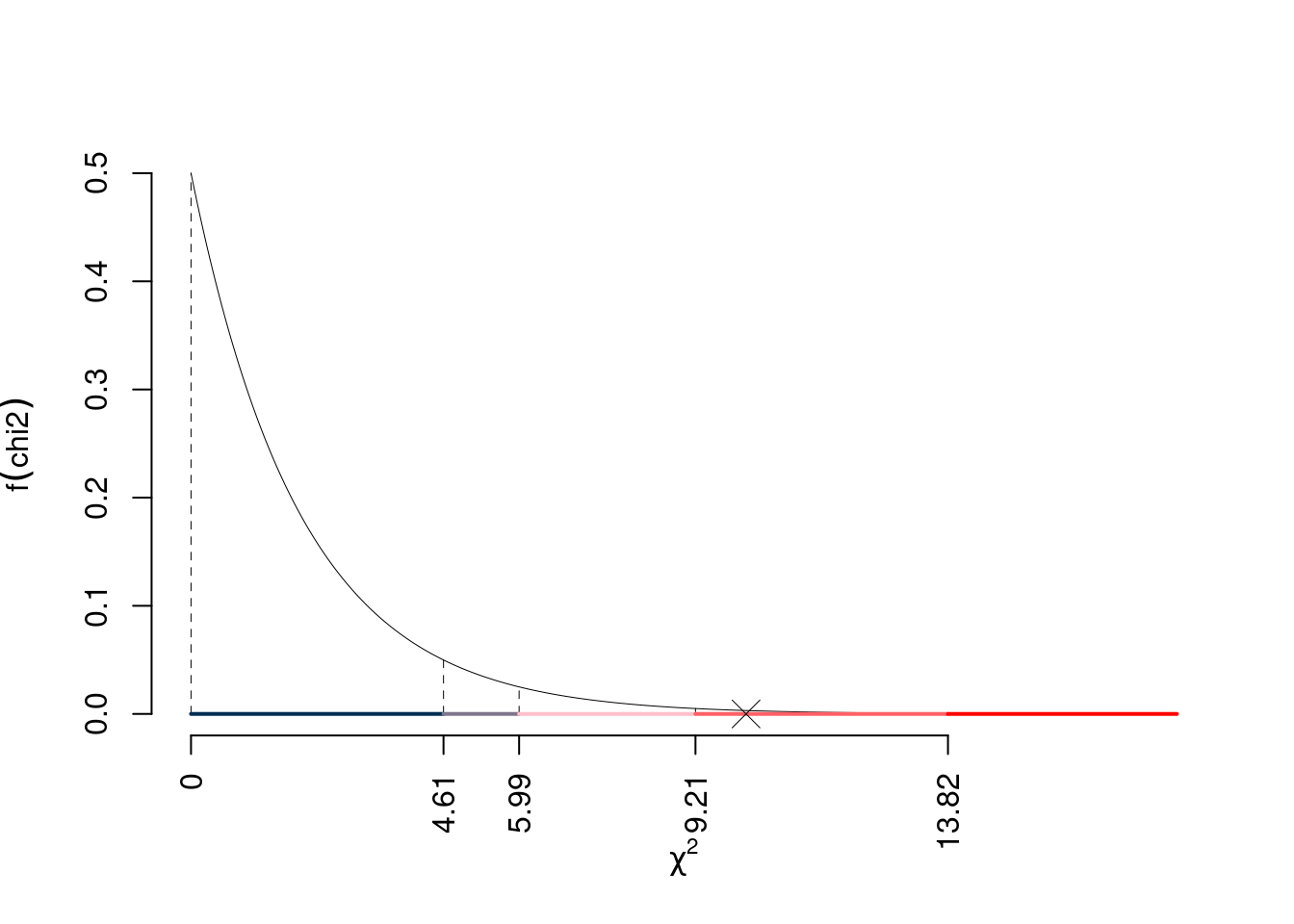
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(\chi^2_{2}>10.13)=0.00631391090280442 \]
Attenzione il calcolo del \(p_\text{value}\) con la distribuzione \(\chi^2\) è puramente illustrativo e non può essere riprodotto senza una calcolatrice statistica adeguata.\[ 0.001 \leq p_\text{value}= 0.006314 < 0.01 \]
Esercizio 2
L’Associazione dei Ristoranti dell’Emilia Romagna ha condotto un’indagine sulle preferenze culinarie dei clienti dei ristoranti della regione. Durante una settimana, sono stati intervistati 300 clienti di vari ristoranti. L’associazione è interessata a capire se le preferenze dei clienti per le tipologie di cucina offerte differiscono dalla media nazionale.
Qui di seguito è riportata la tabella delle preferenze dei clienti dei ristoranti dell’Emilia Romagna e le percentuali nazionali:
| Italiana | Giapponese | Messicana | Mediterranea | Vegetariana | Totale | |
|---|---|---|---|---|---|---|
| Dati Associazione | \(147\) | \(74\) | \(15\) | \(59\) | \(6\) | \(301\) |
| Media Nazionale | \(40\%\) | \(15\%\) | \(5\%\) | \(35\%\) | \(5\%\) | \(100\%\) |
Testare l’ipotesi che le preferenze dei clienti dei bar dell’Emilia Romagna per le bevande differiscano dalla media nazionale.
Test \(\chi^2\) per conformità
\(\fbox{A}\) Formulazione delle ipotesi \[ \{H_0:\pi_\text{ Dati Associazione }= \pi_\text{ Media Nazionale },~~\forall j \] \(\fbox{B}\) Scelta e calcolo della statistica test.
Si tratta di un test chi quadro di conformità. \[ n^*_j = n\cdot \pi^*_{\text{ Media Nazionale },j} \]
La tabella delle distanze:
| Italiana | Giapponese | Messicana | Mediterranea | Vegetariana | Tot | |
|---|---|---|---|---|---|---|
| Dati Associazione | 147.000 | 74.00 | 15.0000 | 59.00 | 6.000 | 301.00 |
| Media Nazionale | 0.400 | 0.15 | 0.0500 | 0.35 | 0.050 | 1.00 |
| \(n_j^*\) | 120.400 | 45.15 | 15.0500 | 105.35 | 15.050 | 301.00 |
| \(\chi^2\) | 5.877 | 18.43 | 0.0002 | 20.39 | 5.442 | 50.15 |
\[ \chi^2_{obs}= 50.15 \]
i \(gdl\)
\[ ( 5 -1)= 4 \]
\(\fbox{C}\) CONCLUSIONE
I valori critici sono
\(\chi^2_{4;0.1}=7.7794\); \(\chi^2_{4;0.05}=9.4877\); \(\chi^2_{4;0.01}=13.2767\); \(\chi^2_{4;0.001}=18.4668\)
Siccome \(\chi^2_\text{obs}=50.1457>18.4668\), quindi rifiuto \(H_0\) sotto all’1‰, \(p_\text{value}<0.001\),
estremamente significativo \(\fbox{***}\).
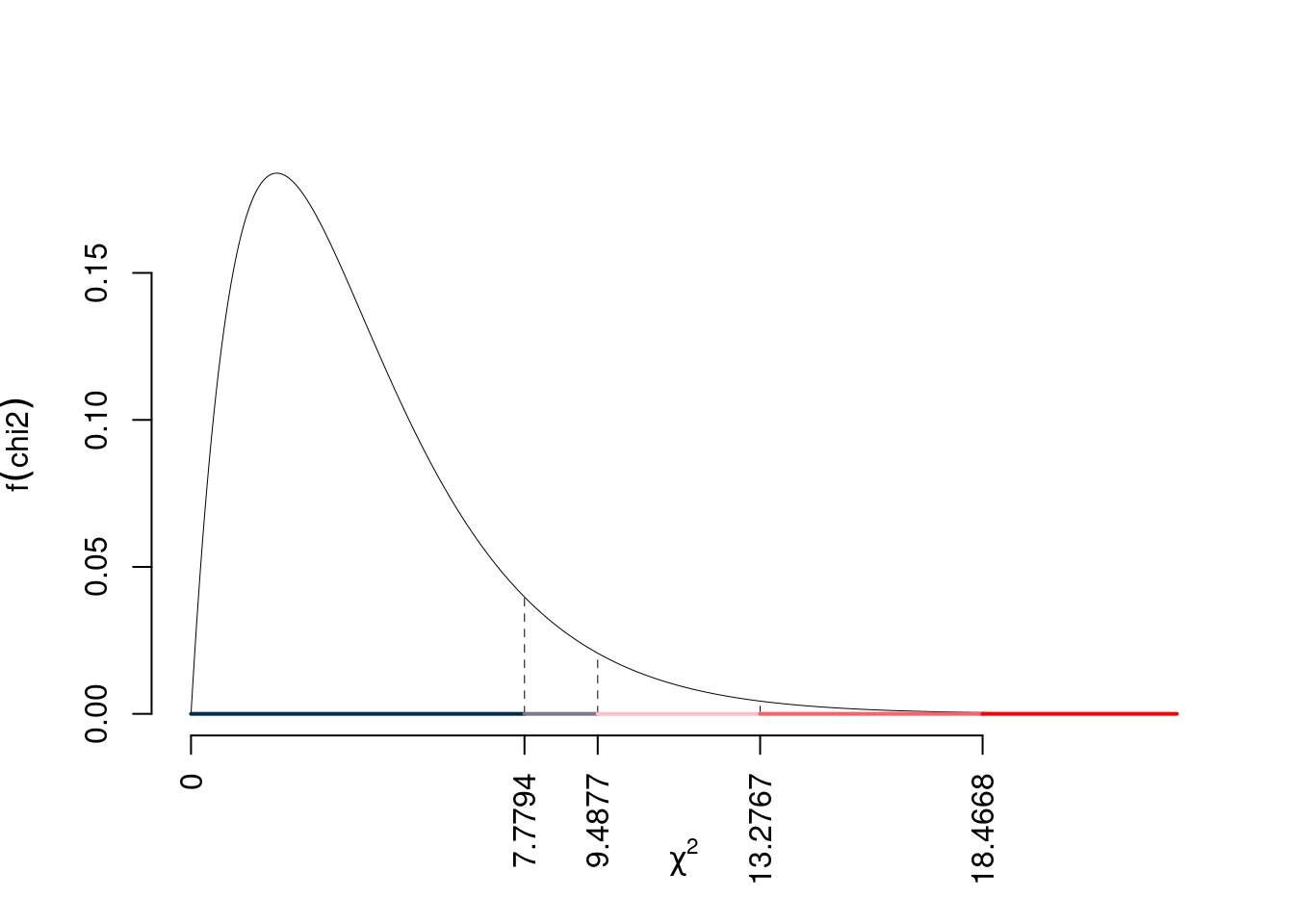
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(\chi^2_{4}>50.15)=0.000000000335962035968862 \]
Attenzione il calcolo del \(p_\text{value}\) con la distribuzione \(\chi^2\) è puramente illustrativo e non può essere riprodotto senza una calcolatrice statistica adeguata.\[ 0 \leq p_\text{value}= 0.000000000336 < 0.001 \]