Anno 2021
Prova di Statistica 2021/06/11-1
Esercizio 1
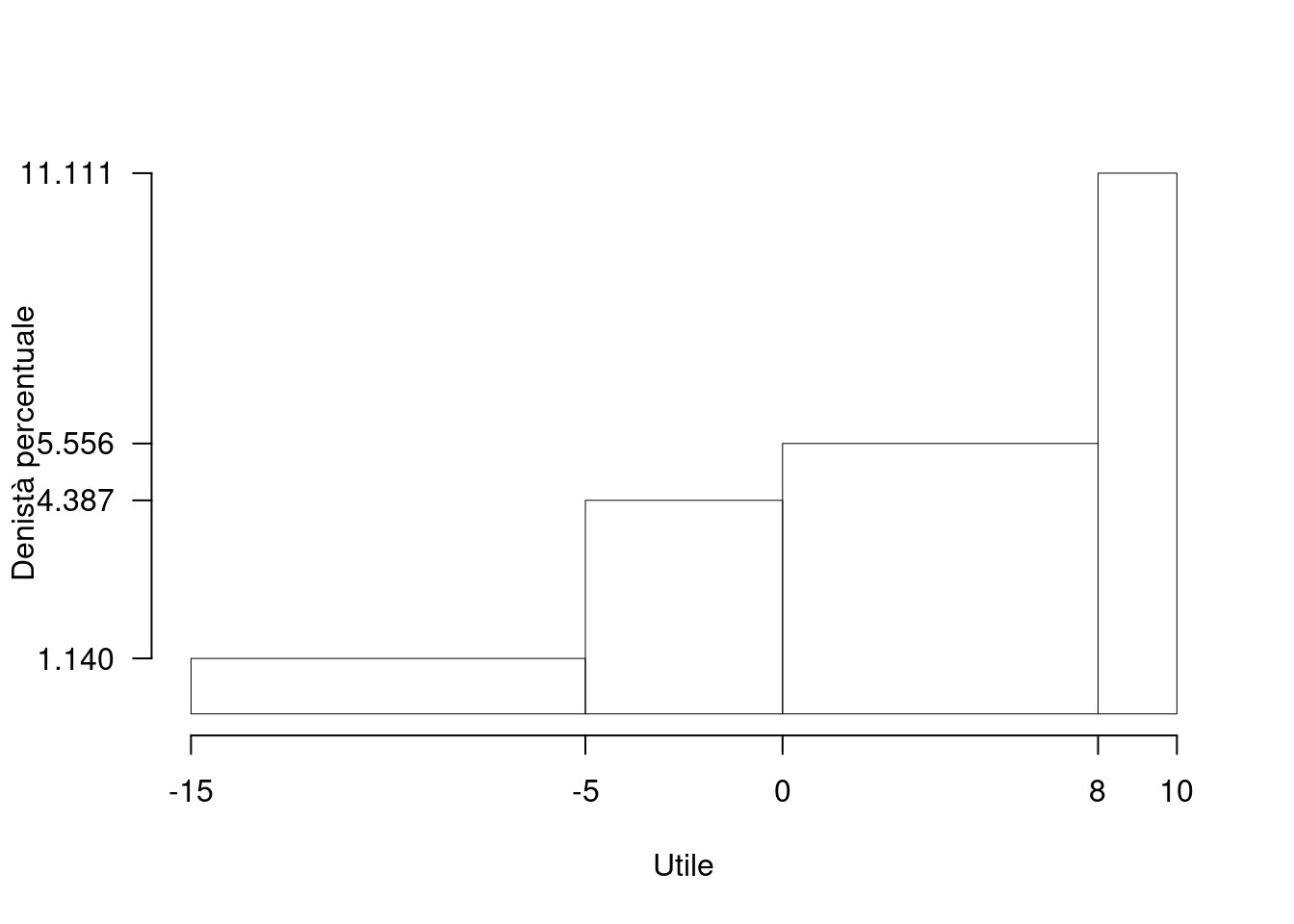
Su un campione di \(350\) aziende è stato rilevato l’utile del 2020, espresso in centinaia di migliaia euro; qui di seguito l’istogramma di densità percentuale.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(h_j\) |
|---|---|---|
| -15 | -5 | 1.140 |
| -5 | 0 | 4.388 |
| 0 | 8 | 5.556 |
| 8 | 10 | 11.111 |
1.a (Punti 14) Calcolare il valore approssimato della mediana.
Per individuare il 75-esimo percentile dobbiamo: \[ b_j=x_{j+1}-x_{j} \] le frequenze relative, \[ f_j=h_j\cdot b_j, \] le cumulate \[ F_j=f_1+...+f_j \] ricostruire la tabella
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(h_j\) | \(b_j\) | \(f_j\) | \(F_j\) |
|---|---|---|---|---|---|
| -15 | -5 | 1.140 | 10 | 0.1140 | 0.1140 |
| -5 | 0 | 4.388 | 5 | 0.2194 | 0.3333 |
| 0 | 8 | 5.556 | 8 | 0.4444 | 0.7778 |
| 8 | 10 | 11.111 | 2 | 0.2222 | 1.0000 |
| 25 | 1.0000 |
\[\begin{eqnarray*} p &=& 0.75, \text{essendo }F_{3}=0.7778 >0.75 \Rightarrow j_{0.75}=3\\ x_{0.75} &=& x_{\text{inf};3} + \frac{ {0.75} - F_{2}} {f_{3}} \cdot b_{3} \\ &=& 0 + \frac {{0.75} - 0.3333} {0.4444} \cdot 8 \\ &=& 7.5 \end{eqnarray*}\]
1.b (Punti 3) Qual è il numero di imprese con utile negativo?
\[\begin{eqnarray*} \%(X> 0 ) &=& ( 0 - 0 )\times h_{ 2 }+ f_{ 3 }\times 100+f_{ 4 }\times 100 \\ &=& ( 0 )\times 4.388 + ( 0.4444 )\times 100+( 0.2222 )\times 100 \\ &=& 0.6667 \times(100)\\ \#(X> 0 ) &=& 233.3 \end{eqnarray*}\]
1.c (Punti 2) (Punti 2) L’utile medio è pari a \(\bar x=2.1688\), e la sua standard deviation \(\sigma_X=6.1222\). Se l’utile \(X\) viene trasformato in perdita \(Y\), \[ Y=-X, \] quanto valgono la media \(\bar y\) e la deviazione standard \(\sigma_Y\) di \(Y\)?.
\[ \bar y=-\bar x=-2.1688 \] mentre \[ \sigma_Y=\sigma_X=6.1222 \]
Esercizio 2
Nel supermercato \(S\) ci sono 4 casse \(C_1\), \(C_2\), \(C_3\) e \(C_4\). A mezzogiorno il numero di persone in fila ogni cassa è descritto da un Poisson di parametro 0.5, \(C_i\sim\text{Pois}(0.5),~i=1,...,4\). Si assume l’indipendenza tra le variabili.
2.a (Punti 14) Calcolare la probabilità che le persone totali (\(C_1+...+C_4\)) in fila al supermercato a mezzogiorno, siano almeno due.
\[ X=C_1+...+C_4\sim \text{Pois}(2) \] e quindi
\[\begin{eqnarray*} P(X\ge 2)&=&1-P(X< 2)\\ &=&1-(P(X=0)+P(X=1))\\ &=&1-(0.1353+0.2707)\\ &=&0.594 \end{eqnarray*}\]
2.b (Punti 3) Qual è la probabilità di avere esattamente due casse su quattro senza fila?
Posto \[ \pi = P(C_i=0)=\frac {0.5}{0!}e^{-0.5}=0.6065 \] la VC \(X\) che conta il numero di casse con zero persone in fila su 4 \[ X\sim\text{Binom}(4,0.6065) \] e quindi \[ P(X=2)={4\choose 2}0.6065^2(1-0.6065)^{4-2}=0.3417 \]
2.c (Punti 3) Quando due eventi \(A\) e \(B\) si dicono indipendenti e quando incompatibili?
Se \(A\) e \(B\) sono incompatibili allora \[ P(A\cap B)=0, \] mentre se \(A\) e \(B\) sono indipendenti allora \[ P(A\cap B)=P(A)P(B), \]
2.d (Punti 2) Se \(X_1\sim N(2,1)\), \(X_2\sim N(1,1)\) e \(X_3\sim N(1,1)\), \(X_1\), \(X_2\) e \(X_3\) indipendenti, come si distribuisce
\[ Y=X_1-(X_2+X_3) ~~~? \]
\[Y\sim N(2-(1+1),1+1+1)\sim N(0,3)\]
Esercizio 3
(Punti 14) Un’urna contiene \(4\) bussolotti Rossi, \(3\) bussolotti Blu e \(5\) bussolotti Gialli. Si estrae 60 volte con reintroduzione; qual è la probabilità che il numero di rossi in 60 estrazioni sia maggiore di 21?
\[\pi=\frac 4{12}=\frac 13\] Teorema del Limite Centrale (somma di Bernoulli)
Siano \(X_1\),…,\(X_n\), \(n=60\) VC IID, tc \(X_i\sim\text{Ber}(\pi=0.3333)\)\(,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\pi,n\pi(1-\pi)) \\ &\sim & N(60\cdot0.3333,60\cdot0.3333\cdot(1-0.3333)) \\ &\sim & N(20,13.33) \end{eqnarray*}\]
\[\begin{eqnarray*} P(S_n > 21) &=& P\left( \frac {S_n - n\pi}{\sqrt{n\pi(1-\pi)}} > \frac {21 - 20}{\sqrt{13.3333}} \right) \\ &=& P\left( Z > 0.27\right) \\ &=& 1-P(Z< 0.27 )\\ &=& 1-\Phi( 0.27 ) \\ &=& 0.3936 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(h\) uno stimatore per theta, tale che \[ E(h)=\theta+\frac\theta {\sqrt{ n}} \] \(h\) è corretto? \(h\) è asintoticamente corretto?
\(h\) non è corretto, infatti \[ E(h)=\theta+\frac\theta {\sqrt{ n}}\neq\theta \] \(h\) è asintoticamente corretto, infatti \[ \lim_{n\to\infty}E(h)=\lim_{n\to\infty}\left(\theta+\frac\theta {\sqrt{ n}}\right)=\theta+0=\theta \]
4.b (Punti 3) Siano \(h_1\) e \(h_2\) due stimatori per \(\theta\), tali che: \[\begin{eqnarray*} MSE(h_1) &=& \frac\theta n\\ MSE(h_2) &=& \frac{2\theta} n \end{eqnarray*}\] Quale dei due stimatori è più efficiente? Perché?
\(h_1\) è più efficiente di \(h_2\), infatti \[\begin{eqnarray*} MSE(h_1) &=& \frac\theta n\\ MSE(h_2) &=& \frac{2\theta} n =2\cdot MSE(h_1)>MSE(h_1) \end{eqnarray*}\]
4.c (Punti 3) Si sono osservati due gruppi di dati quantitativi e si è osservato, \(\hat\mu_1=10.2\) e \(\hat\mu_2=15.6\). Posto a test \[ \begin{cases} H_0:\mu_1=\mu_2\\ H_1:\mu_1\ne \mu_2 \end{cases} \] è risultato \(p_\text{value}=0.0612\). La differenza tra \(\hat\mu_1\) e \(\hat\mu_2\) è significativa? Perché?
Il \(p_\text{value}\) è maggiore di 0.05, la differenza non è significativa per ogni livello di significatività.
Esercizio 5
(Punti 14) In uno studio comparato sui livelli di occupazione femminile, nel comune \(A\) sono state intervistate 50 donne e 30 hanno dichiarato di avere un lavoro stabile; nel comune \(B\) sono state intervistate 60 donne e 40 hanno dichiarato di avere un lavoro stabile.
Testare all’1% l’ipotesi che la proporzione di donne che hanno un lavoro stabile nel comune \(A\) sia uguale a quelle del come \(B\), contro l’alternativa che siano diverse.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\pi_\text{A} = \pi_\text{ B}\text{}\\ H_1:\pi_\text{A} \neq \pi_\text{ B}\text{} \end{cases}\] Siccome \(H_1\) è bilaterale, considereremo \(\alpha/2\), anziché \(\alpha\)
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)
\[\hat\pi_\text{A}=\frac{s_\text{A}}{n_\text{A}}=\frac{30}{50}=0.6\qquad \hat\pi_\text{B}=\frac{s_\text{B}}{n_\text{B}}=\frac{40}{60}=0.6667\]
Calcoliamo la proporzione comune sotto \(H_0\) \[ \pi_C=\frac{s_\text{A}+s_\text{B}}{n_\text{A}+n_\text{B}}= \frac{70}{110}=0.6364 \]
\[\begin{eqnarray*} \frac{\hat\pi_\text{A} - \hat\pi_\text{B}} {\sqrt{\frac {\pi_C(1-\pi_C)}{n_\text{A}}+\frac {\pi_C(1-\pi_C)}{n_\text{B}}}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ (0.6- 0.6667)} {\sqrt{\frac{0.6364(1-0.6364)}{50}+\frac{0.6364(1-0.6364)}{60}}} = -0.7237\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(z_{0.005} = -2.5758\). \[z_{\text{obs}} = -0.7237 > z_{0.005} = -2.5758\]
CONCLUSIONE: i dati sono coerenti con \(H_{0}\) al LdS del 1%
Graficamente
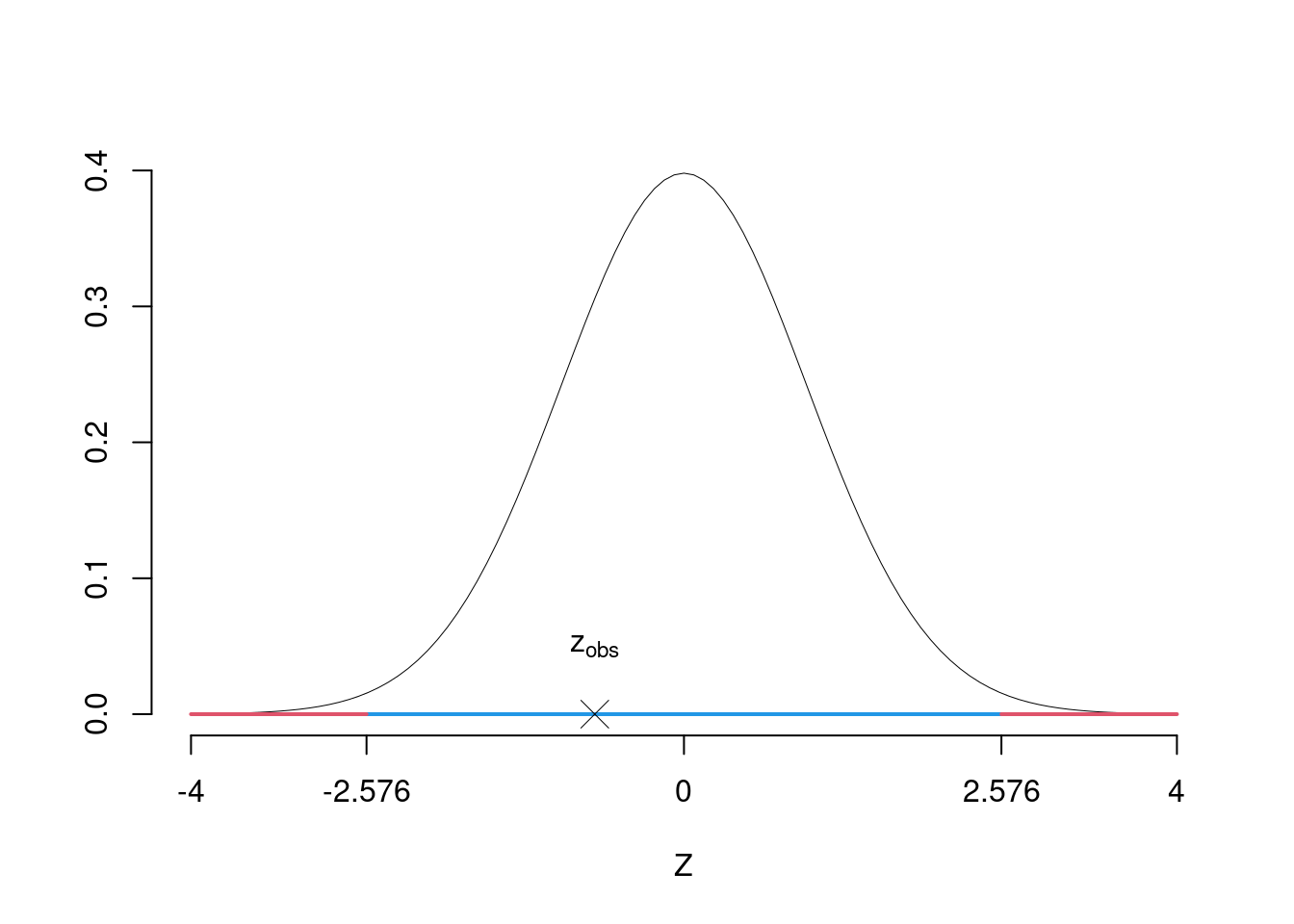
Il \(p_{\text{value}}\) è \[P(|Z|>|z_{\text{obs}}|)=2P(Z>|z_{\text{obs}}|)=2P(Z>| -0.72 |)= 0.4692\]
Esercizio 6
In uno studio sulle competenze scolastiche dei quindicenni si sono analizzati \(n=150\) ragazzi sui quali sono stati registrati i voti di un test in matematica \(X\) e i voti in un test di scienze \(Y\). Qui di seguito le statistiche di interesse:
\[\begin{align*} \sum_{i=1}^n x_i &= 1085, &\sum_{i=1}^n x_i^2 &= 8100 \\ \sum_{i=1}^n y_i &= 969, &\sum_{i=1}^n y_i^2 &= 6578 \\ \sum_{i=1}^n x_iy_i &= 7240. \\ \end{align*}\]
Si consideri il modello di regressione dove \(Y\) viene spiegata da \(X\)
6.a (Punti 14) Prevedere il voto nel test di scienze per uno studente che ha ottenuto 6 nel test di matematica.
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{150} 1085 = 7.2333\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{150} 969 = 6.46\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{150} 8100 - 7.2333 ^2=1.6789\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{150} 6578 - 6.46 ^2=2.1217\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{150} 7240- 7.2333 \cdot 6.46 =1.5361\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{1.5361}{1.6789} = 0.915\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 6.46- 0.915 \times 7.2333 =-0.1583 \end{eqnarray*}\]
6.b (Punti 3) Calcolare la percentuale di varianza spiegata dal modello.
\[\begin{eqnarray*} r&=&\frac{\text{cov}(X,Y)}{\sigma_X\sigma_Y}=\frac{ 1.536 }{ 1.296 \times 1.457 }= 0.8139 \\r^2&=& 0.6624 < 0.75 \end{eqnarray*}\] Il modello non si adatta bene ai dati.
6.c (Punti 3) Discutere il qq-plot dei residui
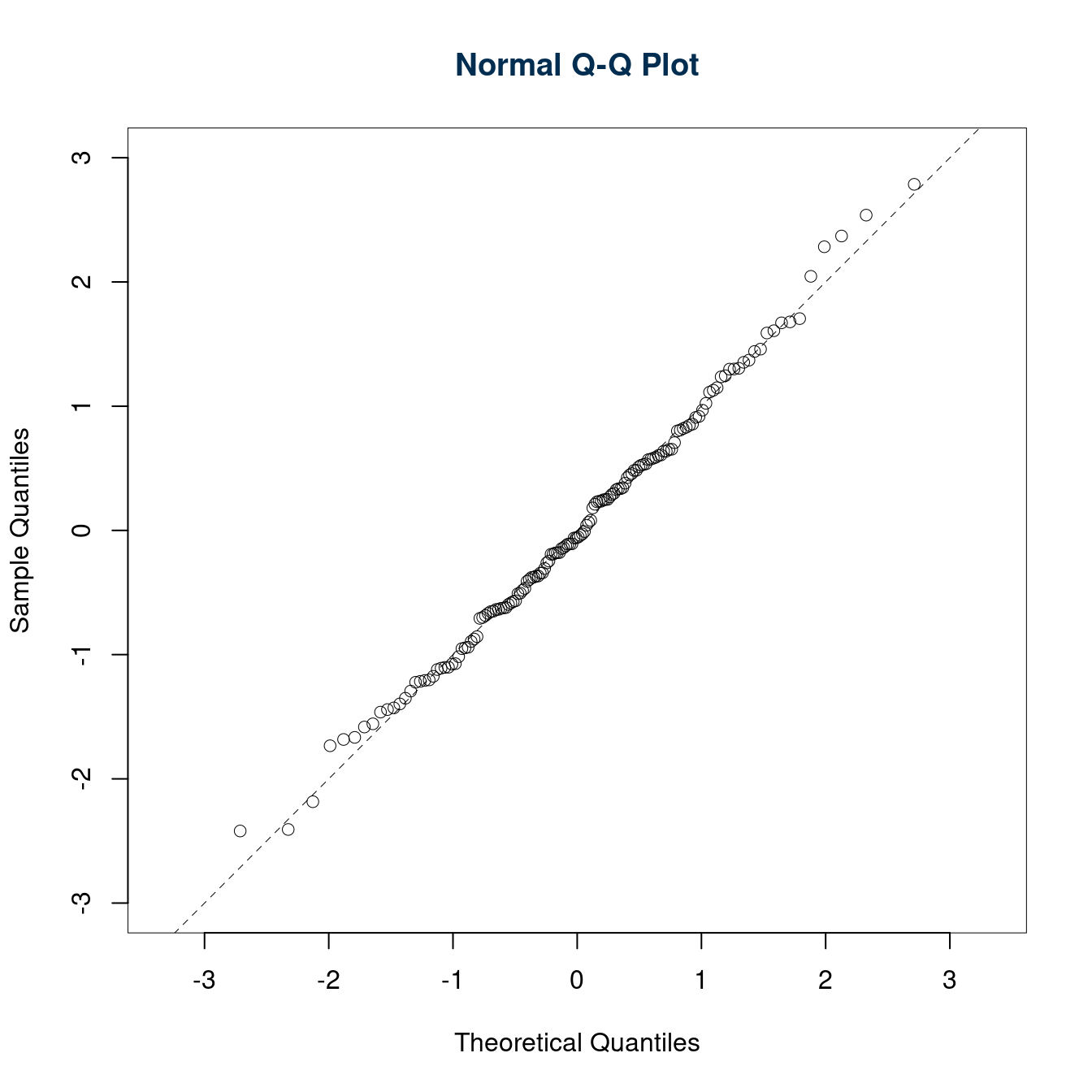
I punti sono be allineati sulla bisettrice degli assi, l’ipotesi di normalità dei residui è rispettata.
6.d (Punti 2) Cosa vuol dire che \(r\) è un numero puro?
Significa che è privo di unità di misura.
Prova di Statistica 2021/06/11-2
Esercizio 1
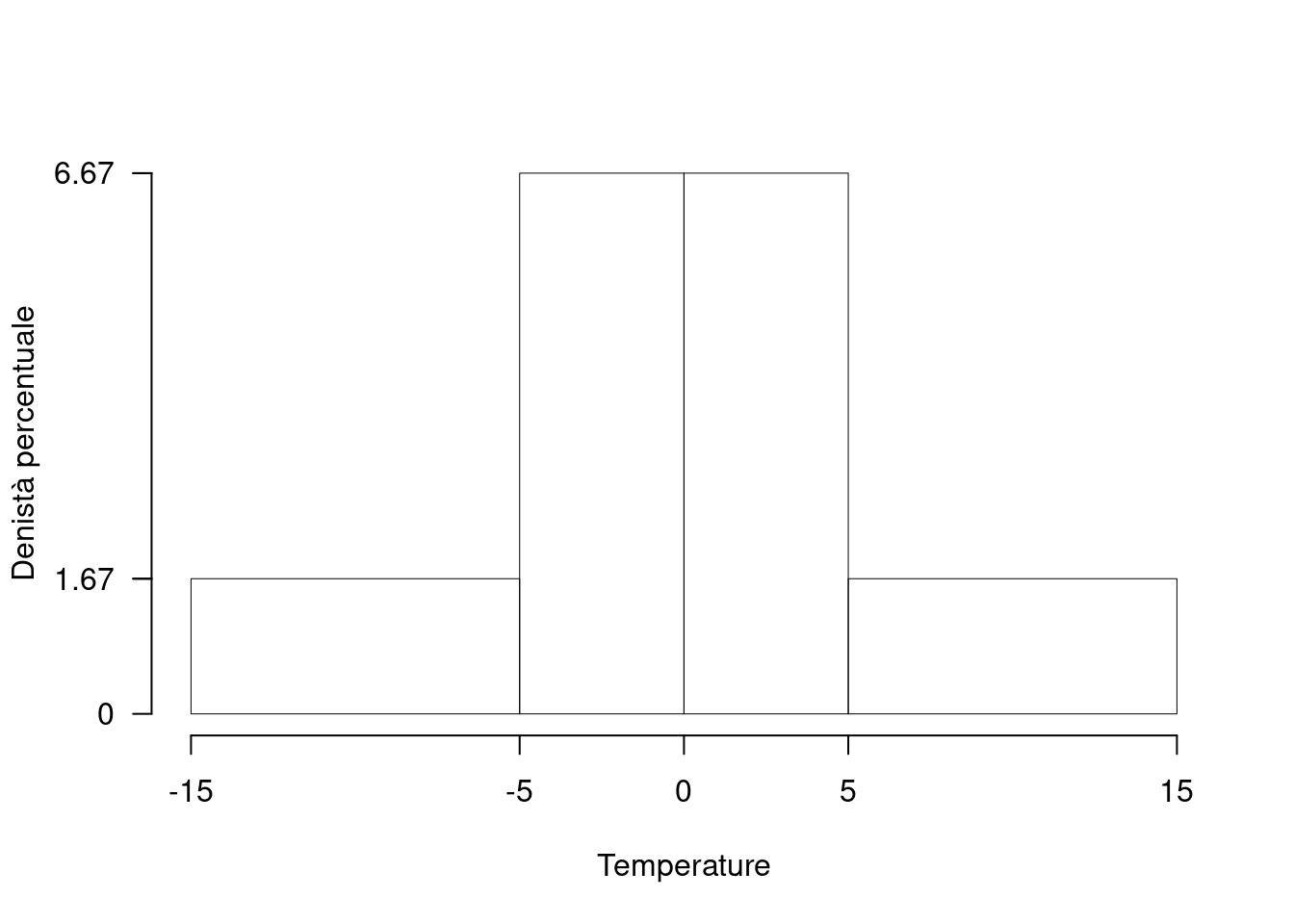
Sono state registrate le temperature del comune \(C\) per \(n=200\) giorni. Qui di seguito l’istogramma di densità percentuale.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(h_j\) |
|---|---|---|
| -15 | -5 | 1.667 |
| -5 | 0 | 6.667 |
| 0 | 5 | 6.667 |
| 5 | 15 | 1.667 |
1.a (Punti 14) Calcolare il valore approssimato del 25-esimo percentile.
Per individuare il 25-esimo percentile dobbiamo: \[ b_j=x_{j+1}-x_{j} \] le frequenze relative, \[ f_j=h_j\cdot b_j, \] le cumulate \[ F_j=f_1+...+f_j \] ricostruire la tabella
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(h_j\) | \(b_j\) | \(f_j\) | \(F_j\) |
|---|---|---|---|---|---|
| -15 | -5 | 1.667 | 10 | 0.1667 | 0.1667 |
| -5 | 0 | 6.667 | 5 | 0.3333 | 0.5000 |
| 0 | 5 | 6.667 | 5 | 0.3333 | 0.8333 |
| 5 | 15 | 1.667 | 10 | 0.1667 | 1.0000 |
| 30 | 1.0000 |
\[\begin{eqnarray*} p &=& 0.25, \text{essendo }F_{2}=0.5 >0.25 \Rightarrow j_{0.25}=2\\ x_{0.25} &=& x_{\text{inf};2} + \frac{ {0.25} - F_{1}} {f_{2}} \cdot b_{2} \\ &=& -5 + \frac {{0.25} - 0.1667} {0.3333} \cdot 5 \\ &=& -3.75 \end{eqnarray*}\]
1.b (Punti 3) Analizzando l’istogramma, individuare il valore della media aritmetica e della mediana.
L’istogramma è perfettamente simmetrico \[ \bar x\approx x_{0.5}\approx 0 \]
1.c (Punti 2) Qual è la percentuale di dati compresa tra il 25-esimo e il 75-esimo percentile?
Per definizione \[\begin{eqnarray*} \%(X\le x_{0.25})&=&25\%\\ \%(X\le x_{0.75})&=&75\%, \qquad\text{e quindi}\\ \%(x_{0.25}< X\le x_{0.75})&=&50\% \end{eqnarray*}\]
Esercizio 2
Il flusso giornaliero d’acqua in entrata nella vasca \(V\) è descritto da una variabile casuale normale \(X_E\sim N(5.1,1.1)\), il flusso giornaliero in uscita è descritto da una variabile casuale normale \(X_U\sim N(6.2,0.5)\).
La variazione di livello nella vasca è dunque data da: \[ X_L=X_E-X_U. \] 2.a (Punti 14) Calcolare la probabilità che la variazione di livello sia negativa (\(X_L<0\)).
La variazione di livello nella vasca si distribuisce \[ X_L=X_E-X_U\sim N(5.1-6.2;1.1+0.5) \] E quindi
\[\begin{eqnarray*} P(X_L < 0) &=& P\left( \frac {X_L - \mu}{\sigma} < \frac {0 - ( -1.1 )}{\sqrt{1.6}} \right) \\ &=& P\left( Z < 0.87\right) \\ &=& \Phi( 0.87 ) \\ &=& 0.8078 \end{eqnarray*}\]
2.b (Punti 3) Nell’ipotesi di indipendenza tra i giorni, calcolare la probabilità di avere esattamente due giorni su cinque con livello negativo.
Posto \[ \pi = P(X_L=0)=0.8077 \] la VC \(X\) che conta il numero di giorni con livello negativo in 5 giorni \[ X\sim\text{Binom}(5,0.8077) \] e quindi \[ P(X=2)={5\choose 2}0.8077^2(1-0.8077)^{5-2}=0.0464 \]
2.c (Punti 3) Se \(P(A)=0.6\) e \(P(B)=0.8\), \(A\) e \(B\) possono essere incompatibili?
No, perché se fossero incompatibili allora \[ P(A\cup B)=P(A)+P(B)=0.6+0.8=1.4>1 \] che è impossibile.
2.d (Punti 2) Se \(X\sim N(\mu_X,\sigma^2_X)\) come si distribuisce \[Y=\left(\frac{X-\mu_X}{\sigma_X}\right)^2 ~~~?\]
Anzitutto osserviamo che \[ Z=\frac{X-\mu_X}{\sigma_X}\sim N(0,1) \] Poi che \[ Y=Z^2\sim\chi_1^2 \]
Esercizio 3
(Punti 14) Un’urna contiene \(4\) bussolotti numerati con \(\fbox{−1}\), \(3\) numerati con \(\fbox{0}\) e \(4\) numerati con \(\fbox{+1}\). Si estrae 60 volte con reintroduzione; qual è la probabilità che la media delle 60 estrazioni sia minore di 0.1?
\[\begin{eqnarray*} \mu &=& E(X_i) = \sum_{x\in S_X}x P(X=x)\\ &=& ( -1 ) \frac { 4 }{ 11 }+ 0 \frac { 3 }{ 11 }+ 1 \frac { 4 }{ 11 } \\ &=& 0 \\ \sigma^2 &=& V(X_i) = \sum_{x\in S_X}x^2 P(X=x)-\mu^2\\ &=&\left( ( -1 ) ^2\frac { 4 }{ 11 }+ 0 ^2\frac { 3 }{ 11 }+ 1 ^2\frac { 4 }{ 11 } \right)-( 0 )^2\\ &=& 0.7273 \end{eqnarray*}\] Teorema del Limite Centrale (media VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=60\) VC IID, tc \(E(X_i)=\mu=0\) e \(V(X_i)=\sigma^2=0.7273,\forall i\), posto: \[ \bar X=\frac{S_n}n =\frac{X_1 + ... + X_n}n \] allora:\[\begin{eqnarray*} \bar X & \mathop{\sim}\limits_{a}& N(\mu,\sigma^2/n) \\ &\sim & N\left(0,\frac{0.7273}{60}\right) \\ &\sim & N(0,0.01212) \end{eqnarray*}\]
\[\begin{eqnarray*} P(\bar X < 0.1) &=& P\left( \frac {\bar X - \mu}{\sqrt{\sigma^2/n}} < \frac {0.1 - 0}{\sqrt{0.0121}} \right) \\ &=& P\left( Z < 0.91\right) \\ &=& \Phi( 0.91 ) \\ &=& 0.8186 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(h\) uno stimatore per \(\theta\), tale che \[ MSE(h)=\frac\theta {\sqrt{ n}}+\frac1n \] \(h\) è consistente? Perché?
Sì, è consistente, infatti \[ \lim_{n\to\infty}MSE(h)=\lim_{n\to\infty}\left(\frac\theta {\sqrt{ n}}+\frac1n\right)=0 \]
4.b (Punti 3) Siano \(X_1,...,X_n\) \(n\) VC IID, replicazioni di \(X\sim \mathscr{L}(\theta)\) e sia \(\hat\theta\) lo stimatore di massima verosimiglianza per \(\theta\), \(\hat\theta\) è corretto?
No, in generale \(\hat\theta\) non è corretto, ad esempio \[ E(\hat\sigma^2)=\frac{n-1}n\sigma^2\ne\sigma^2 \] ma lo è sempre asintoticamente \[ \lim_{n\to\infty}E(\hat\theta)=\theta \] ad esempio: \[ \lim_{n\to\infty}E(\hat\sigma^2)=\lim_{n\to\infty}\frac{n-1}n\sigma^2=\sigma^2 \]
4.c (Punti 3) Definire la significatività e la potenza di un test.
La probabilità di significatività è definita con \(\alpha\) e rappresenta la probabilità di rifiutare \(H_0\) quando è vera \[\alpha=P(\text{Errore I tipo})=P(\text{Decidere $H_1$};H_0)\]
La potenza del test è definita \[1-\beta =P(\text{Decidere $H_1$}; H_1)\]
Cioè la probabilità di scegliere \(H_1\) quando \(H_1\) è vera.
Esercizio 5
(Punti 14) In uno studio comparato sul reddito femminile, nel comune \(A\) sono state intervistate 15 donne e si è osservato un reddito medio pari a \(\bar x_A=23.2\) mila euro lordi annui con una standard deviation pari a \(\hat\sigma_A=2.2\); nel comune \(B\) sono state intervistate 18 donne e si è osservato un reddito medio pari a \(\bar x_B=20.1\) mila euro lordi annui con una standard deviation pari a \(\hat\sigma_B=1.8\).
Sotto ipotesi di omogeneità, testare all’1% l’ipotesi che il reddito medio femminile nel comune \(A\) sia uguale a quello del comune \(B\), contro l’alternativa che siano diversi.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0:\mu_\text{A} = \mu_\text{ B}\text{}\\ H_1:\mu_\text{A} \neq \mu_\text{ B}\text{} \end{cases}\] Siccome \(H_1\) è bilaterale, considereremo \(\alpha/2\), anziché \(\alpha\)
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(T\)
L’ipotesi è di omogeneità e quindi calcoliamo:
\[ S_p^2=\frac{n_\text{A}\hat\sigma^2_\text{A}+n_\text{B}\hat\sigma^2_\text{B}}{n_\text{A}+n_\text{B}-2} = \frac{15\cdot2.2^2+18\cdot1.8^2}{15+18-2}=4.2232 \]
\[\begin{eqnarray*} \frac{\hat\mu_\text{A} - \hat\mu_\text{B}} {\sqrt{\frac {S^2_p}{n_\text{A}}+\frac {S^2_p}{n_\text{B}}}}&\sim&t_{n_\text{A}+n_\text{B}-2}\\ t_{\text{obs}} &=& \frac{ (23.2- 20.1)} {\sqrt{\frac{4.2232}{15}+\frac{4.2232}{18}}} = 4.3148\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(t_{(15+18-2);\, 0.005} = 2.744\). \[t_{\text{obs}} = 4.3148 > t_{31;\, 0.005} = 2.744\]
CONCLUSIONE: i dati sono coerenti con \(H_{0}\) al LdS del 1%
Graficamente
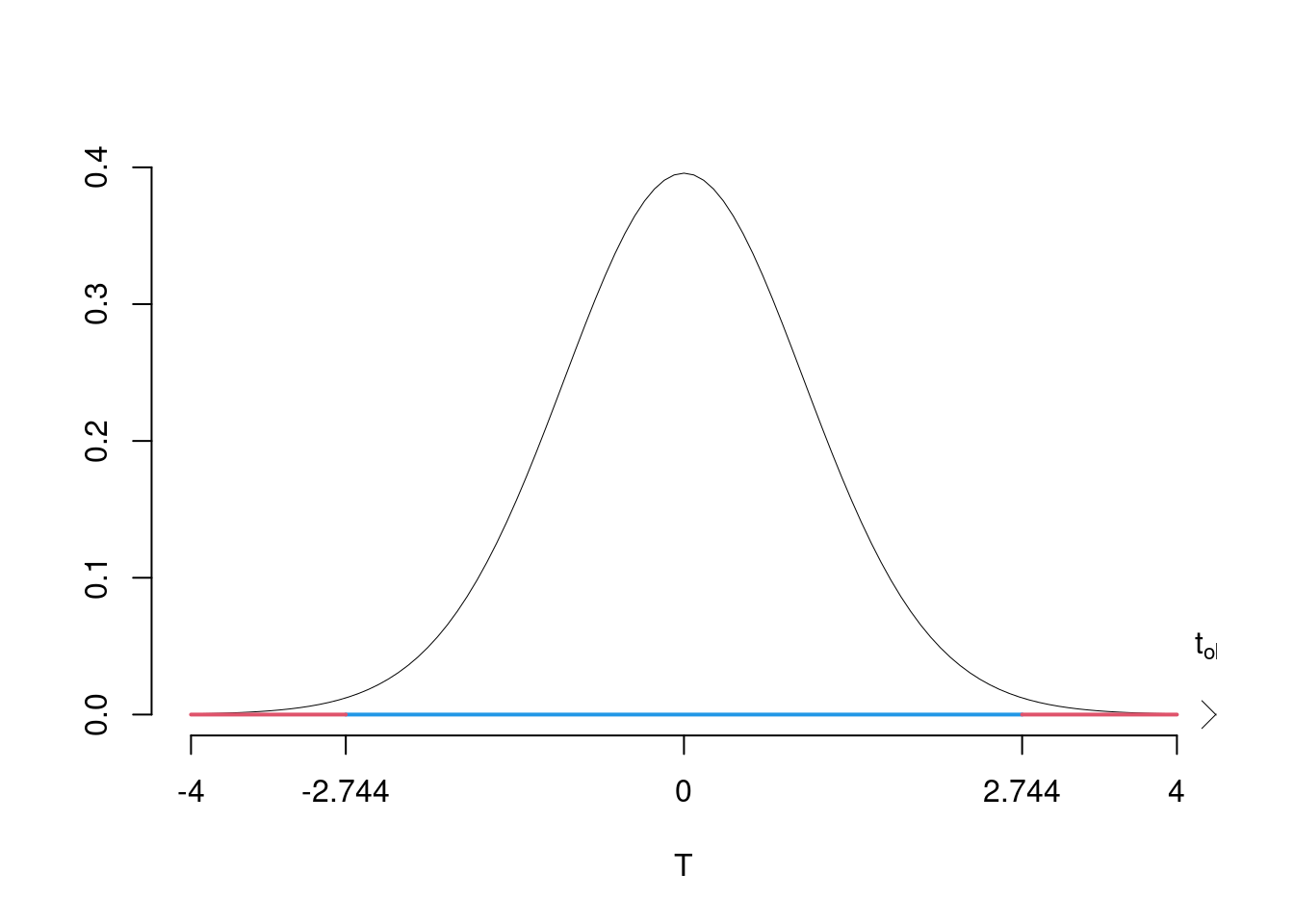
Il \(p_{\text{value}}\) è \[P(|T_{n1+n2-2}|>|t_{\text{obs}}|)=2P(T_{n1+n2-2}>|t_{\text{obs}}|)=2P(T_{n1+n2-2}>| 4.3148 |)= 0.0001512\]
Esercizio 6
In uno studio sulle competenze scolastiche dei quindicenni si sono analizzati \(n=150\) ragazzi sui quali sono stati registrati il numero di libri in casa \(X\) (espresso in decine di libri) e i voti in un test di comprensione \(Y\). Qui di seguito le statistiche di interesse:
\[\begin{align*} \sum_{i=1}^n x_i &= 1129, &\sum_{i=1}^n x_i^2 &= 8823 \\ \sum_{i=1}^n y_i &= 1014, &\sum_{i=1}^n y_i^2 &= 7151 \\ \sum_{i=1}^n x_iy_i &= 7923. \\ \end{align*}\]
Si consideri il modello di regressione dove \(Y\) viene spiegata da \(X\)
6.a (Punti 14) Si osservino le prime 5 coppie di dati| i | Libri | Voto |
|---|---|---|
| 1 | 5.006 | 4.504 |
| 2 | 5.108 | 4.557 |
| 3 | 5.126 | 4.618 |
| 4 | 5.155 | 4.691 |
| 5 | 5.187 | 4.644 |
Calcolare il residuo per il quarto dato.
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{150} 1129 = 7.5267\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{150} 1014 = 6.76\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{150} 8823 - 7.5267 ^2=2.1693\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{150} 7151 - 6.76 ^2=1.9757\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{150} 7923- 7.5267 \cdot 6.76 =1.9398\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{1.9398}{2.1693} = 0.8942\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 6.76- 0.8942 \times 7.5267 =0.0296 \end{eqnarray*}\]
\[\begin{eqnarray*} \hat y_i &=&\hat\beta_0+\hat\beta_1 x_i=\\ &=& 0.02957 + 0.8942 \times 5.1551 = 4.639 \\ \hat \varepsilon_i &=& y_i-\hat y_i\\ &=& 4.691 - 4.639 = 0.05186 \end{eqnarray*}\]
6.b (Punti 3) Il modello si adatta bene ai dati?
Il modello spiega il \(r^2\times100=(0.937)^2\times 100=87.7948\%>75\%\) della viarbilità totale di \(Y\). Sì, il modello spiega bene i dati.
6.c (Punti 3) Discutere il diagramma dei residui
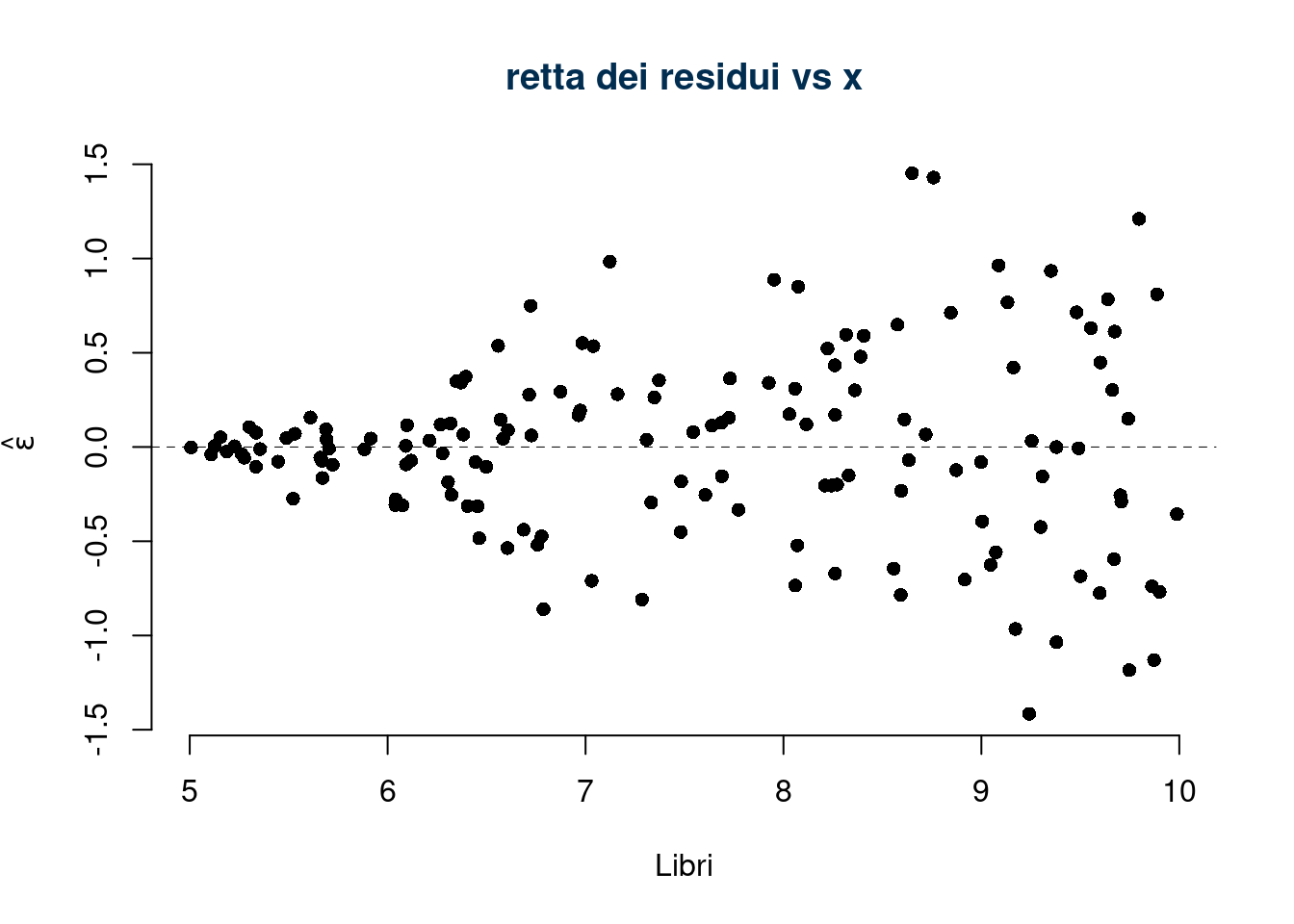
La variabilità dei residui cresce al crescere dalla x, l’ipotesi di omoschedasticità è chiaramente violata.
6.d (Punti 2) Quando in un modello di regressione lineare un punto è considerato influente?
La coppia \((x_i,y_i)\) è considerata punto influente se il suo residuo studentizzato è maggiore di un livello soglia deciso sulle tavole della \(t\) con \(n-2\) gradi di libertà: \[|\tilde \varepsilon_i|>t_{n-2,0.05} \]
Prova di Statistica 2021/06/30-1
Esercizio 1
Su un campione di \(350\) aziende è stato rilevato il costo in spese legali (espresso in migliaia di euro). Qui di seguito i dati in classi e le frequenze cumulate:| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(F_j\) |
|---|---|---|
| 0 | 5 | 0.0943 |
| 5 | 8 | 0.4543 |
| 8 | 13 | 0.8171 |
| 13 | 20 | 1.0000 |
1.a (Punti 14) Individuare la classe modale.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(F_j\) | \(f_j\) | \(b_j\) | \(h_j\) |
|---|---|---|---|---|---|
| 0 | 5 | 0.0943 | 0.0943 | 5 | 1.886 |
| 5 | 8 | 0.4543 | 0.3600 | 3 | 12.000 |
| 8 | 13 | 0.8171 | 0.3629 | 5 | 7.257 |
| 13 | 20 | 1.0000 | 0.1829 | 7 | 2.612 |
| 1.0000 | 20 |
e osservare che la classe \([5,8)\) è la classe modale perché è quella con densità maggiore.
1.b (Punti 3) Calcolare la percentuale approssimata di aziende con spese maggiori di 10 mila euro.
\[\begin{eqnarray*} \%(X> 10 ) &=& ( 13 - 10 )\times h_{ 3 }+ f_{ 4 }\times 100 \\ &=& ( 3 )\times 7.257 + ( 0.1829 )\times 100 \\ &=& 0.4006 \times(100)\\ \#(X> 10 ) &=& 140.2 \end{eqnarray*}\]
1.c (Punti 3) Calcolare la percentuale approssimata di aziende con spese maggiori di 10 mila euro.
La mediana \(x_{0.5}\) è il minimante
\[ \sum_{i=1}^n|x_i-x_{0.5}|<\sum_{i=1}^n|x_i-x^*|, ~~\forall x^*\neq x_{0.5} \]
Esercizio 2
L’urna \(A\) contiene 4 palline numerate: \(\fbox{-1},\fbox{0},\fbox{0},\fbox{+1}\).
L’urna \(B\) contiene 3 palline numerate: \(\fbox{0},\fbox{1},\fbox{2}\).
Si estrae dall’urna \(A\) e dall’urna \(B\) e si sommano i due numeri
2.a (Punti 14) Calcolare la probabilità che la somma dei numeri sia maggiore uguale a 2.
\[ \begin{array}{ r|rrrrrr } & -1 ;&\color{blue}{ \frac{ 1 } { 4 }} & 0 ;&\color{blue}{ \frac{ 2 } { 4 }} & 1 ;&\color{blue}{ \frac{ 1 } { 4 }} \\ \hline 1 ;\color{blue}{ 1 / 3 }& 0;&\color{red}{\frac{1}{12}}& 1;&\color{red}{\frac{2}{12}}& 2;&\color{red}{\frac{1}{12}}\\ 2 ;\color{blue}{ 1 / 3 }& 1;&\color{red}{\frac{1}{12}}& 2;&\color{red}{\frac{2}{12}}& 3;&\color{red}{\frac{1}{12}}\\ \end{array} \]
E ricaviamo la distribuzione di, \(X\)
\[ \begin{array}{ r|rrrr } X & 0& 1& 2& 3 \\ \hline P(X) & \frac{2}{12}& \frac{4}{12}& \frac{4}{12}& \frac{2}{12} \\ \end{array} \] Calcoliamo valore atteso e varianza
\[\begin{eqnarray*} \mu &=& E(X_i) = \sum_{x\in S_X}x P(X=x)\\ &=& 0 \frac { 2 }{ 12 }+ 1 \frac { 4 }{ 12 }+ 2 \frac { 4 }{ 12 }+ 3 \frac { 2 }{ 12 } \\ &=& 1.5 \\ \sigma^2 &=& V(X_i) = \sum_{x\in S_X}x^2 P(X=x)-\mu^2\\ &=&\left( 0 ^2\frac { 2 }{ 12 }+ 1 ^2\frac { 4 }{ 12 }+ 2 ^2\frac { 4 }{ 12 }+ 3 ^2\frac { 2 }{ 12 } \right)-( 1.5 )^2\\ &=& 0.9167 \end{eqnarray*}\] \[ P(S\ge 2)=3/12+1/12=4/12=1/3 \]
2.b (Punti 3) Calcolare la probabilità che la somma sia maggiore uguale a 1 dato che dall’urna \(A\) è uscito \(\fbox{0}\).
Dalla definizione stessa di probabilità condizionata \[\begin{eqnarray*} P(X\geq 1|X_A=0)&=&\frac{P(\{X\geq 1\}\cap\{X_A=0\})}{P(\{X_A=0\})}\\ &=&\frac{2/12+2/12}{2/4}\\ &=&4/12\cdot4/2\\ &=&0.6667 \end{eqnarray*}\]
2.c (Punti 3) Sia \(X\sim \text{Pois}(10)\) e \(Y\sim\text{Binom}(n,0.5)\). Sia \[ W=X-Y \] Calcolare il valore atteso \(E(W)\) e la varianza \(V(W)\) di \(W\).
Osserviamo \[\begin{align*} E(X)&=10 &E(Y)&=n\cdot 0.5\\ V(X)&=10 &V(Y)&=n\cdot0.5(1-0.5) \end{align*}\] e quindi \[\begin{eqnarray*} E(W)&=&E(X)-E(Y)\\ &=&10-n\cdot 0.5\\ V(W)&=&V(X)+V(Y),\qquad\text{se e solo se $X$ e $Y$ sono indipendenti}\\ &=&10+n\cdot 0.25 \end{eqnarray*}\]
2.d (Punti 2) Siano \(X_1,...,X_6\), \(6\) variabili casuali IID, tali che \[ X_i\sim N\left(2.5,3^2\right). \] Come si distribuisce \[ Y=\sum_{i=1}^6\left(\frac{X_i-2.5}{3}\right)^2~~? \]
Si osserva \[ Z_i=\frac{X_i-2.5}{3}\sim N(0,1) \] e quindi \[ Y=(Z_1^2+...+Z_6^2)\sim\chi_6^2 \]
Esercizio 3
(Punti 14) Si lancia un dado perfetto, si vince se esce un numero maggiore o uguale a 5. Si gioca \(n=64\) volte, qual è la probabilità di vincere più di 23 volte su 64 giocate?
\[ \pi=\frac 2 6=\frac 13 \] la probabilità di vincere all’estrazione \(i\), e quindi \(X_i\sim\text{Ber}(\pi)\)
\[\begin{eqnarray*} E(X_i)&=&\pi\\ V(X_i)&=&\pi(1-\pi) \end{eqnarray*}\]
In virtù del TCL della somma di n VC IID
Teorema del Limite Centrale (somma di Bernoulli)
Siano \(X_1\),…,\(X_n\), \(n=64\) VC IID, tc \(X_i\sim\text{Ber}(\pi=0.3333)\)\(,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\pi,n\pi(1-\pi)) \\ &\sim & N(64\cdot0.3333,64\cdot0.3333\cdot(1-0.3333)) \\ &\sim & N(21.33,14.22) \end{eqnarray*}\]
\[\begin{eqnarray*} P(S_n > 23) &=& P\left( \frac {S_n - n\pi}{\sqrt{n\pi(1-\pi)}} > \frac {23 - 21.3333}{\sqrt{14.2222}} \right) \\ &=& P\left( Z > 0.44\right) \\ &=& 1-P(Z< 0.44 )\\ &=& 1-\Phi( 0.44 ) \\ &=& 0.33 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(h\) uno stimatore per \(\theta\), tale che \[\begin{eqnarray*} E(h)&=&\theta+\frac\theta {\sqrt{ n}}\\ V(h)&=&\frac{\theta^2}{\sqrt n} \end{eqnarray*}\] \(h\) è consistente?
Uno stimatore è consistente se \[ \lim_{n\to\infty} MSE(h)=0 \] Essendo \[\begin{eqnarray*} MSE(h)&=&V(h)+B^2(h)\\ &=&V(h)+|E(h)-\theta|^2\\ &=&\frac{\theta^2}{\sqrt n}+\left|\theta+\frac\theta {\sqrt{ n}}-\theta\right|^2\\ &=&\frac{\theta^2}{\sqrt n}+\frac{\theta^2} { n}\\ \lim_{n\to\infty} \left(\frac{\theta^2}{\sqrt n}+\frac{\theta^2} { n}\right)&=&0 \end{eqnarray*}\] Quindi sì, \(h\) è consistente.
4.b (Punti 3) Definire la funzione di verosimiglianza.
Siano \(x_1,...,x_n\) \(n\) osservazioni di \(X\sim \mathscr{L}(\theta)\), \(\theta\in\Theta\), si definisce la verosimiglianza \(L\) di \(\theta\) la funzione: \[L(\theta;x_1,...,x_n)=L(\theta)\propto P(X_1=x_1,...,X_n=x_n;\theta)\]
Se \(x_1,..,x_n\) sono osservazioni \(IID\) otteniamo \[\begin{eqnarray*} L(\theta) &\propto& P(X_1=x_1;\theta)\cdot...\cdot P(X_n=x_n;\theta) \\ &\propto& \prod_{i=1}^n f(x_i;\theta) \end{eqnarray*}\]
4.c (Punti 3) Si sono osservati due gruppi di dati quantitativi e si è osservato, \(\hat\mu_1=10.2\), \(\hat\sigma_1=1.12\) e \(\hat\mu_2=15.6\), \(\hat\sigma_2=3.72\). Posto a test \[ \begin{cases} H_0:\sigma_1=\sigma_2\\ H_1:\sigma_1\ne \sigma_2 \end{cases} \] è risultato \(p_\text{value}=0.0012\). I due gruppi sono da considerare omogenei o eterogenei? Perché?
Il \(p_\text{value}=0.0012\) ci indica che i dati supportano \(H_1\), quindi i due gruppi sono da considerarsi eterogenei.
Esercizio 5
(Punti 14) In uno studio sui consumi sono stati intervistati \(n=25\) individui sui quali è stato rilevato il reddito mensile \(X\) (in migliaia di euro), e il consumo \(Y\) (in migliaia di euro). Il modello di regressione \[ Y_i=\beta_0+\beta_1 x_i+\varepsilon_i \] ha fornito i seguenti risultati
\[\begin{align*} \hat\beta_0&=0.60, &\hat\beta_1&=0.75, &r&=0.87\\ \bar x&=1.61 &\hat \sigma_X&=0.90\\ \bar y&=1.81 &\hat \sigma_Y&=0.78\\ \end{align*}\]
Testare al 5% l’ipotesi che il consumo di sussistenza \(\beta_0\) sia uguale 0.5 contro l’alternativa che sia maggiore.
\[\begin{eqnarray*} \hat{\sigma_\varepsilon}^2&=&(1-r^2)\hat\sigma_Y^2\\ &=& (1-0.7569)\times0.6084\\ &=& 0.1479\\ S_\varepsilon^2 &=& \frac{n} {n-2} \hat{\sigma_\varepsilon}^2\\ &=& \frac{25} {25-2} \hat{\sigma_\varepsilon}^2 \\ &=& \frac{25} {25-2} \times 0.1479 = 0.1608 \end{eqnarray*}\]
E quindi
\[\begin{eqnarray*} V(\hat\beta_{0}) &=& \sigma_{\varepsilon}^{2} \left( \frac{1} {n} + \frac{\bar{x}^{2}} {n \hat{\sigma}^{2}_{X}} \right)\\ \widehat{V(\hat\beta_{0})} &=& S_{\varepsilon}^{2}\left( \frac{1} {n} + \frac{\bar{x}^{2}} {n \hat{\sigma}^{2}_{X}} \right)\ \\ &=& 0.1608\times\left( \frac{1} {25} + \frac{1.61^{2}} {25\times 0.81} \right)\\ \widehat{SE(\hat\beta_{0})} &=& \sqrt{0.027}\\ &=& 0.1643 \end{eqnarray*}\]
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\beta_{0} = 0.5\\ H_1:\beta_{0} > 0.5 \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(T\) Test su un coefficiente di regressione: \(\Rightarrow\) t-Test.
\[\begin{eqnarray*} \frac{\hat\beta_{0} - \beta_{0;H_0}} {\widehat{SE(\hat\beta_{0})}}&\sim&t_{n-2}\\ t_{\text{obs}} &=& \frac{ (0.6- 0.5)} {0.1643} = 0.6085\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(t_{(25-2);\, 0.05} = 1.7109\). \[t_{\text{obs}} = 0.6085 < t_{23;\, 0.05} = 1.7109\] CONCLUSIONE: i dati sono coerenti con \(H_{0}\) al LdS del 5%
Graficamente
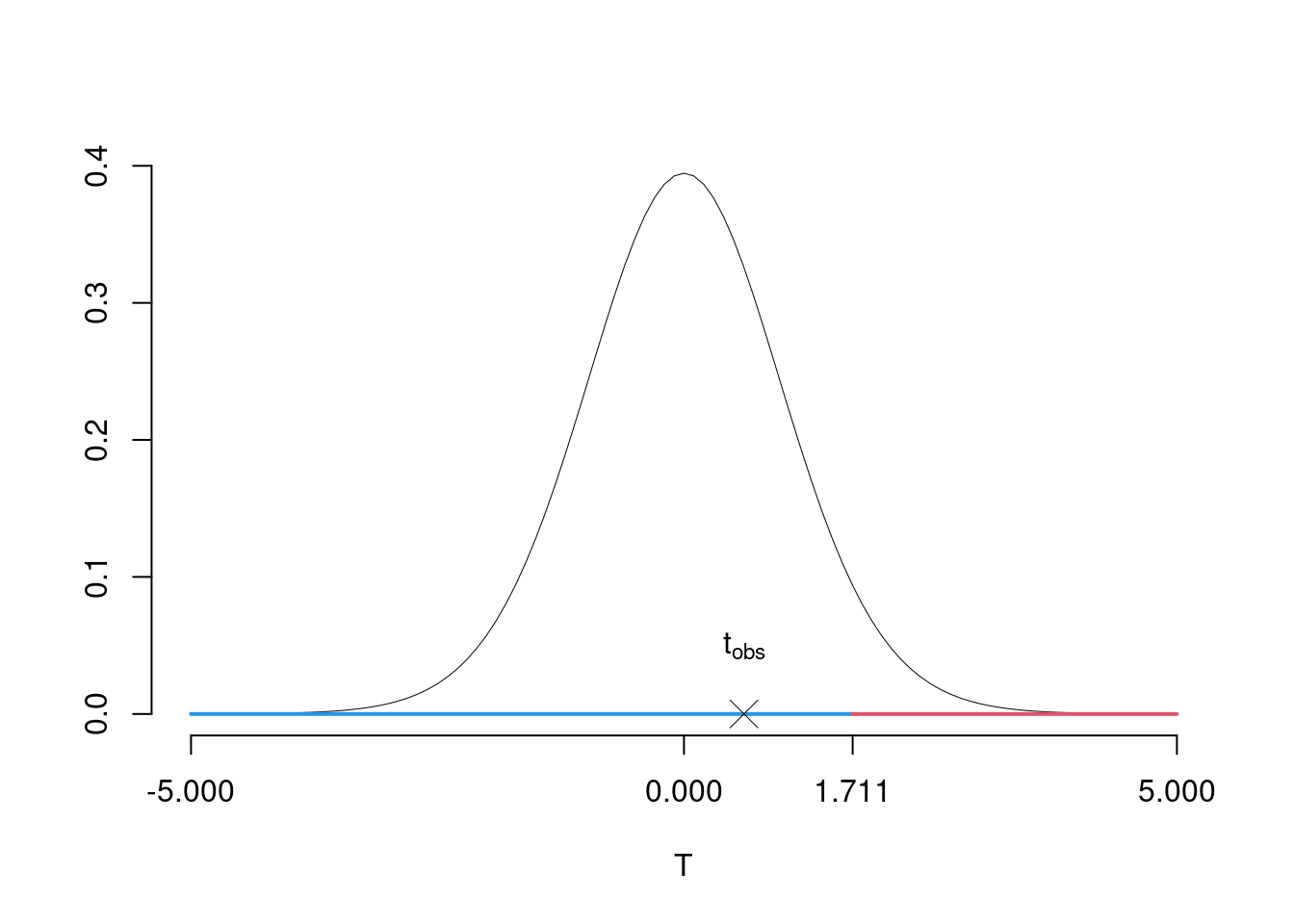
Il \(p_{\text{value}}\) è \[P(T_{n-2}>t_{\text{obs}})=P(T_{n-2}> 0.608 )= 0.2744\]
Esercizio 6
In uno studio sui consumi sono stati intervistati \(n=75\) individui sui quali è stato rilevato il reddito mensile \(X\) (in migliaia di euro), e il consumo \(Y\) (in migliaia di euro). Il modello di regressione. Qui di seguito le statistiche di interesse:
\[\begin{align*} \bar x&=4.126 &\hat \sigma_X&=2.6036, &x_{(0)}&=0.0052, &x_{(n)}&=9.5485,\\ \bar y&=3.5691 &\hat \sigma_Y&=2.6833, &y_{(0)}&=0.0718, &y_{(n)}&=11.008,\\ \text{cov}(X,Y)&=5.8726. \end{align*}\]
Si consideri il modello di regressione dove \(Y\) viene spiegata da \(X\)
6.a (Punti 14) Prevedere il consumo per un individuo che guadagna \(x=4.126\) e per un individuo che guadagna \(x=12.3\).
\[\begin{eqnarray*} \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{5.8726}{0.81} = 0.8604\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 3.5733-0.8604\times 1.61=0.6 \end{eqnarray*}\]\[\hat y_{X= 12.3 }=\hat\beta_0+\hat\beta_1 x= 0.6 + 0.8604 \times 12.3 = 11.18 \]
6.b (Punti 3) Quale delle due previsioni, per \(x=4.126\) e per \(x=12.3\), è più affidabile? Perché?
L’errore di previsione per \(x\) dipende dalla sua distanza quadratica dalla media \[ \text{err prev}(x)=V(\hat Y_{(X=x)})=\sigma_{\varepsilon}^{2}\left(\frac 1n+\frac{(x-\bar x)^2} {n \hat{\sigma}^{2}_{X}} \right) \] quindi l’errore di previsione è minimo per \(x=4.126\), mentre \(x=12.3>x_{(n)}=9.5485\) e si tratta di estrapolazione.
La previsione per \(x=4.126\) è molto più affidabile che quella per \(x=12.3\).
6.c (Punti 3) Calcolare le quantità \(TSS\), \(RSS\) e \(ESS\).
Ricaviamo \(R^2\) \[R^2=\left(\frac{5.8726}{2.6036\cdot 2.6833}\right)^2=0.87^2=0.7569\] quindi \[\begin{eqnarray*} TSS &=& n\hat\sigma^2_Y\\ &=& 75 \times 0.6084 \\ &=& 45.63 \\ ESS &=& R^2\cdot TSS\\ &=& 0.7569 \cdot 45.63 \\ &=& 34.54 \\ RSS &=& (1-R^2)\cdot TSS\\ &=& (1- 0.7569 )\cdot 45.63 \\ &=& 11.09 \\ TSS &=& RSS+TSS \\ 45.63 &=& 34.54 + 11.09 \end{eqnarray*}\]
6.d (Punti 2) Cosa vuol dire che \(r\) è invariante ai cambiamenti di scala?
\[\text{se }W=a+bY,\text{allora }r_{X,W}=\text{sign}(b) r_{XY},\text{ dove la funzione sign}(b)= \begin{cases}+1, &\text{se $b>0$}\\ -1, &\text{se $b<0$} \end{cases}\]
Prova di Statistica 2021/06/30-2
Esercizio 1
Su un campione di \(12\) famiglie della provincia \(Q\) è stato rilevato il reddito mensile, qui di seguito i dati non ordinati espressi in migliaia di euro al mese.
| \(i\) | \(x_{i}\) | \(i\) | \(x_{i}\) | \(i\) | \(x_{i}\) |
|---|---|---|---|---|---|
| \(1\) | 3.7 | \(5\) | 6.5 | \(9\) | 0.3 |
| \(2\) | 12.6 | \(6\) | 1.6 | \(10\) | 14.0 |
| \(3\) | 4.3 | \(7\) | 4.8 | \(11\) | 17.2 |
| \(4\) | 3.8 | \(8\) | 4.7 | \(12\) | 16.2 |
1.a (Punti 14) Individuare il 25-esimo, 50-esimo e l’75-esimo percentile
| \(i\) | \(x_{i}\) | \(i\) | \(x_{i}\) | \(i\) | \(x_{i}\) |
|---|---|---|---|---|---|
| \((1)\) | 0.3 | \((5)\) | 4.3 | \((9)\) | 12.6 |
| \((2)\) | 1.6 | \((6)\) | 4.7 | \((10)\) | 14.0 |
| \((3)\) | 3.7 | \((7)\) | 4.8 | \((11)\) | 16.2 |
| \((4)\) | 3.8 | \((8)\) | 6.5 | \((12)\) | 17.2 |
e quindi
\[\begin{eqnarray*} x_{0.25} &=& x_{(\lceil n\times0.25\rceil)}=x_{(3)}=3.7\\ x_{0.50} &=& \frac{x_{(n/2)}+x_{(n/2+1)}}{2}=\frac{4.7+4.8}{2} =4.75\\ x_{0.75} &=& x_{(\lceil n\times0.75\rceil)}=x_{(9)}=12.6 \end{eqnarray*}\]
1.b (Punti 3) La somma dei dati è 94.6. Come dobbiamo aspettarci l’istogramma di densità?
La somma dei dati è 94.6 e quindi la media viene \[ \bar x=\frac 1{12}94.6=7.8833 \]
siccome \(\bar x>x_{0.5}\) allora l’istogramma avrà una coda lunga a dx.
1.c (Punti 2) Cosa significa che la media aritmetica gode della proprietà di linearità?
Esercizio 2
Si consideri un’urna così formata, \[ \left\{\fbox{1},\fbox{2},\fbox{3},\fbox{4},\fbox{5},\fbox{6},\fbox{7},\fbox{8}\right\}. \] Si vince se si estrae un numero maggiore o uguale a 6.
Si estrae con reintroduzione.
2.a (Punti 14) Qual è la probabilità di vincere almeno 5 volte su 6 estrazioni?
Sia \(X\) la VC che conta il numero di di vittorie in 6 giocate, quindi \(n=6\) replicazioni di una Bernoulli \(X_i\sim\mbox{Ber}(\pi=3/8)\) e quindi
\[ X=X_1+...+X_n\sim\mbox{Binom}(n=6,\pi=0.375) \]
la probabilità di avere almeno 5 bussolotti rossi su 6 estrazioni è
\[\begin{eqnarray*} P( X > 5 ) &=& \binom{ 6 }{ 5 } 0.375 ^{ 5 }(1- 0.375 )^{ 6 - 5 }+\binom{ 6 }{ 6 } 0.375 ^{ 6 }(1- 0.375 )^{ 6 - 6 } \\ &=& 0.0278+0.0028 \\ &=& 0.0306 \end{eqnarray*}\]
2.b (Punti 3) Calcolare la probabilità di vincere la prima volta alla quarta estrazione.
Ogni singola giocata \(X_i\) è una Bernoulli \(X_i\sim\mbox{Ber}(\pi=3/8)\) e quindi \[\begin{eqnarray*} E&=&\text{Vincere la prima volta alla quarta estrazione}\\ &=& X_1=0~\cap~X_2=0~\cap~X_3=0~\cap~X_4=1\\ P(E)&=&P(X_1=0~\cap~X_2=0~\cap~X_3=0~\cap~X_4=1)\\ &=&P(X_1=0)P(X_2=0)P(X_3=0)P(X_4=1)\\ &=&\left(1-\frac 38\right)\left(1-\frac 38\right)\left(1-\frac 38\right)\frac 38\\ &=&\left(\frac 58\right)^3\frac 38\\ &=&0.0916 \end{eqnarray*}\]
2.c (Punti 3) Se \(A\) e \(B\) sono due eventi tali che, \(P(A)>0\), \(P(B)>0\), \(P(A\cap B)=0\). \(A\) e \(B\) possono essere indipendenti?
No, in quanto, se \(A\) e \(B\) sono indipendenti \[P(A\cap B)=P(A)P(B)\neq0\]
2.d (Punti 2) Sia \(X\sim N(3.2,(1.1)^2)\) e sia \(Y\sim\chi_{n-1}^2\), posto \[ T=\frac{\left(\frac{X-3.2}{1.1}\right)}{\sqrt{\frac{Y}{n-1}}}, \] come si distribuisce \(T\)?
Si noti che \[ Z=\left(\frac{X-3.2}{1.1}\right)\sim N(0,1) \] e che \[ T=\frac{Z}{\sqrt{\frac{Y}{n-1}}}\sim t_{n-1} \]
Esercizio 3
(Punti 14) Un’urna contiene un numero imprecisato di palline numerate. Si conoscono solo la media \(\mu=12.3\) e la standard deviation \(\sigma=1.1\) dei numeri delle sfere.
Si estrae \(n=81\) volte con reintroduzione, qual è la probabilità che la media delle 81 estrazioni sia compresa tra 12.06 e 12.54?
Il valore atteso di della \(i\)-esima estrazione è \[ E(X_i)=12.3 \] e la varianza \[ V(X_i)=1.1^2 \]
In virtù del TCL per la media: la media di \(n\) VC IID, tali che \(E(X_i)=\mu\), \(V(X_i)=\sigma^2\)
Teorema del Limite Centrale (media VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=81\) VC IID, tc \(E(X_i)=\mu=12.3\) e \(V(X_i)=\sigma^2=1.21,\forall i\), posto: \[ \bar X=\frac{S_n}n =\frac{X_1 + ... + X_n}n \] allora:\[\begin{eqnarray*} \bar X & \mathop{\sim}\limits_{a}& N(\mu,\sigma^2/n) \\ &\sim & N\left(12.3,\frac{1.21}{81}\right) \\ &\sim & N(12.3,0.01494) \end{eqnarray*}\]
\[\begin{eqnarray*} P(12.06<\bar X\leq 12.54) &=& P\left( \frac {12.06 - 12.3}{\sqrt{0.0149}} < \frac {\bar X - \mu}{\sqrt{\sigma^2/n}} \leq \frac {12.54 - 12.3}{\sqrt{0.0149}}\right) \\ &=& P\left( -1.96 < Z \leq 1.96\right) \\ &=& \Phi(1.96)-\Phi(-1.96)\\ &=& \Phi( 1.96 )-(1-\Phi( 1.96 )) \\ &=& 0.975 -(1- 0.975 ) \\ &=& 0.95 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(h\) uno stimatore per \(\theta\), tale che \[\begin{eqnarray*} E(h)&=&\theta+\frac\theta {n^2},\\ V(h)&=&\frac{\sqrt\theta}{ n}. \end{eqnarray*}\] Ricavare \(MSE(h)\), il Mean Squared Error di \(h\).
\[\begin{eqnarray*} MSE(h)&=&V(h)+B^2(h)\\ &=&V(h)+|E(h)-\theta|^2\\ &=&\frac{\sqrt\theta}{ n}+\left|\theta+\frac\theta {n^2}-\theta\right|^2\\ &=&\frac{\sqrt\theta}{ n}+\frac{\theta^2} { n^4}\\ \end{eqnarray*}\]
4.b (Punti 3) Scrivere la funzione di verosimiglianza di una Poisson.
Siano \(X_1,...,X_n\), \(n\) VC IID, tali che, \(X_i\sim\text{Pois}(\lambda)\) La verosimiglianza è \[\begin{eqnarray*} L(\lambda) &=& \prod_{i=1}^n\frac{\lambda^{x_i}}{x_i!}e^{-\lambda}\\ &\propto& \lambda^{s_n} e^{-n\lambda},\qquad s_n=\sum_{i=1}^n x_i \end{eqnarray*}\]
4.c (Punti 3) Definire il \(p_{\text{value}}\), la probabilità di significatività osservata.
La probabilità di significatività \(p_{\text{value}}\) è
\[p_{\text{value}}=P(|T|>|t_{\text{obs}}|;H_0)\]
La probabilità di significatività osservata \(p_\text{value}\) esprime la probabilità, se fosse vera \(H_0\), di trovare un campione ancora più in favore di \(H_1\) di quello disponile
Esercizio 5
(Punti 14) In uno studio sulle preferenze tra canali televisivi, vengono analizzati 92 individui, classificati canale preferito (RAI, Mediaset, La7) e per titolo di studio superiore (Laureato, Non Laureato)
Qui di seguito i dati dello studio, \[ \begin{array}{l|rrr|r} & \text{Rai} &\text{Mediaset} &\text{La7}& \\ \hline \text{Laureato} &15 &5 &12 &32\\ \text{Non Laureato} &10 &35 &15 &60\\ \hline &25 &40 &27 &92 \end{array} \]
Titolo di studio superiore e canale preferito sono indipendenti?
È un test sull’indipendenza tra due VC
| Rai | Mediaset | La7 | Tot | |
|---|---|---|---|---|
| Laureato | 15 | 5 | 12 | 32 |
| Non Laureato | 10 | 35 | 15 | 60 |
| Tot | 25 | 40 | 27 | 92 |
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[ \Big\{H_0:\pi_{ij}=\pi_{i\bullet}\pi_{\bullet j} \]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(\chi^2\)
Si usa il test \(\chi^2\), si crea la tabella delle frequenze teoriche \[ n_{ij}^*=\frac{n_{i\bullet}n_{\bullet j}}{n} \]
| Rai | Mediaset | La7 | Tot | |
|---|---|---|---|---|
| Laureato | 8.696 | 13.91 | 9.391 | 32 |
| Non Laureato | 16.304 | 26.09 | 17.609 | 60 |
| Tot | 25.000 | 40.00 | 27.000 | 92 |
La tabella delle distanze \[ \frac{(n_{ij}-n_{ij}^*)^2}{n_{ij}^*} \]
| Rai | Mediaset | La7 | Tot | |
|---|---|---|---|---|
| Laureato | 4.571 | 5.710 | 0.725 | 0 |
| Non Laureato | 2.438 | 3.045 | 0.386 | 0 |
| Tot | 0.000 | 0.000 | 0.000 | 0 |
\(\fbox{C}\) DECISIONE
\[ \chi^2_{obs}=16.8747 \]
i \(gdl\)
\[ (3-1)\times(4-1)=6 \]
\(\alpha=0.01\) e quindi \(\chi_{1,0.01}^2=16.8119\)
Essendo \[ \chi^2_{obs}=16.8747 >\chi_{1,0.01}^2=16.8119 \]
allora rifiuto \(H_0\) al lds dell’1 percento.
Graficamente
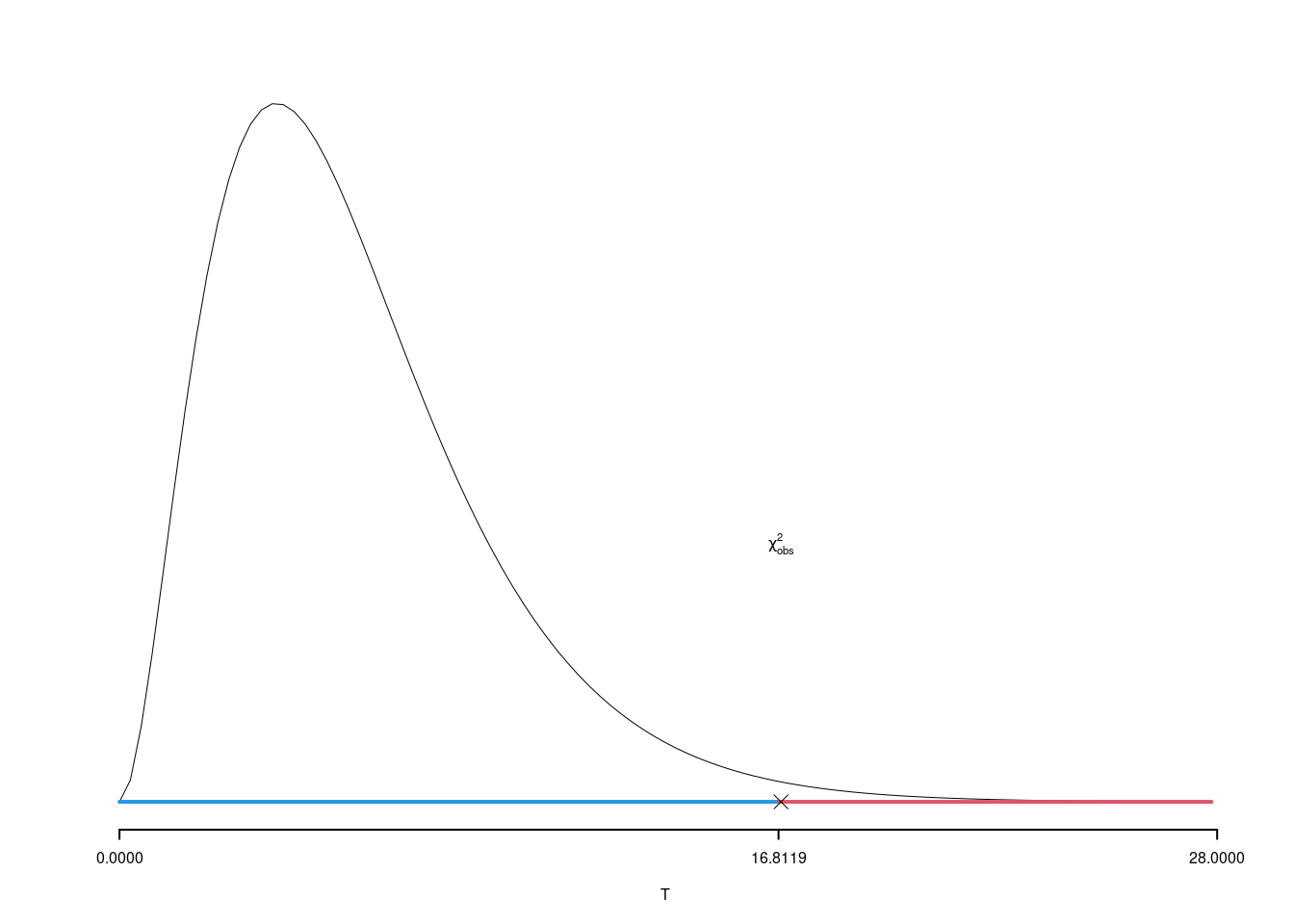
Il \(p_{\text{value}}\) è \[ P(\chi^2_{6}> \chi^2_{\text{obs}})=0.009755 \]
Esercizio 6
In uno studio sulla qualità della vita si è osservato su 4 provincie l’ammontare degli investimenti provinciali pro capite per attività culturali (\(X\)), in centinaia di euro, e un indice di qualità della vita (\(Y\)), espresso in opportuna scala. Qui di seguito i dati| \(i\) | \(x_i\) | \(y_i\) |
|---|---|---|
| 1 | 1 | 4 |
| 2 | 2 | 6 |
| 3 | 4 | 5 |
| 4 | 5 | 8 |
6.a (Punti 14) Stimare il modello di regressione dove la qualità della vita è spiegata dagli investimenti provinciali.
| \(i\) | \(x_i\) | \(y_i\) | \(x_i^2\) | \(y_i^2\) | \(x_i\cdot y_i\) |
|---|---|---|---|---|---|
| 1 | 1 | 4.00 | 1.00 | 18.0 | 4 |
| 2 | 2 | 6.00 | 4.00 | 31.0 | 12 |
| 3 | 4 | 5.00 | 15.00 | 29.0 | 21 |
| 4 | 5 | 8.00 | 27.00 | 56.0 | 39 |
| Totale | 12 | 23.00 | 47.00 | 134.0 | 76 |
| Totale/n | 3 | 5.75 | 11.75 | 33.5 | 19 |
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{92} 12= 3\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{92} 23= 5.75\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{92} 48 -3^2=3\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{92} 134 -5.75^2=0.4375\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{92} 76-3\cdot5.75=1.755\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{1.755}{3} = 0.585\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 5.75-0.585\times 3=3.995 \end{eqnarray*}\]
6.b (Punti 3) Calcolare la percentuale di varianza spiegata dal modello.
Ricaviamo \(R^2\) \[ R^2=\left(\frac{1.755}{1.6163\cdot 1.1819}\right)^2=1.5319^2=2.3467 \] Il modello si adatta molto bene ai dati, spiegando il 234.6686% (>75%) della variabilità totale della Y.
6.c (Punti 3) Ricavare le quantità \(TSS\), \(RSS\) e \(ESS\).
\[\begin{eqnarray*} TSS &=& n\hat\sigma^2_Y\\ &=& 92 \times 0.4375 \\ &=& 40.25 \\ ESS &=& R^2\cdot TSS\\ &=& 2.347 \cdot 40.25 \\ &=& 94.45 \\ RSS &=& (1-R^2)\cdot TSS\\ &=& (1- 2.347 )\cdot 40.25 \\ &=& -54.2 \\ TSS &=& RSS+TSS \\ 40.25 &=& 94.45 + -54.2 \end{eqnarray*}\]
6.d (Punti 2) Cosa significa che gli stimatori di massima dei minimi quadrati \(\hat\beta_0\) e \(\hat\beta_1\) sono BLUE?
Gli stimatori \(\hat\beta_{0}\) e \(\hat\beta_{1}\) di \(\beta_{0}\) e \(\beta_{1}\) sono, tra tutti gli stimatori lineari corretti per \(\beta_0\) e \(\beta_1\), BLUE ( Best Linear Unbiased Estimators Best: i più efficienti; Unbiased: corretti; Linear Estimators: stimatori lineari).
Prova di Statistica 2021/07/22-1
Esercizio 1
Su un campione di \(350\) aziende è stato rilevato il costo annuo in gas metano (espresso in migliaia di euro). Qui di seguito l’istogramma di densità:
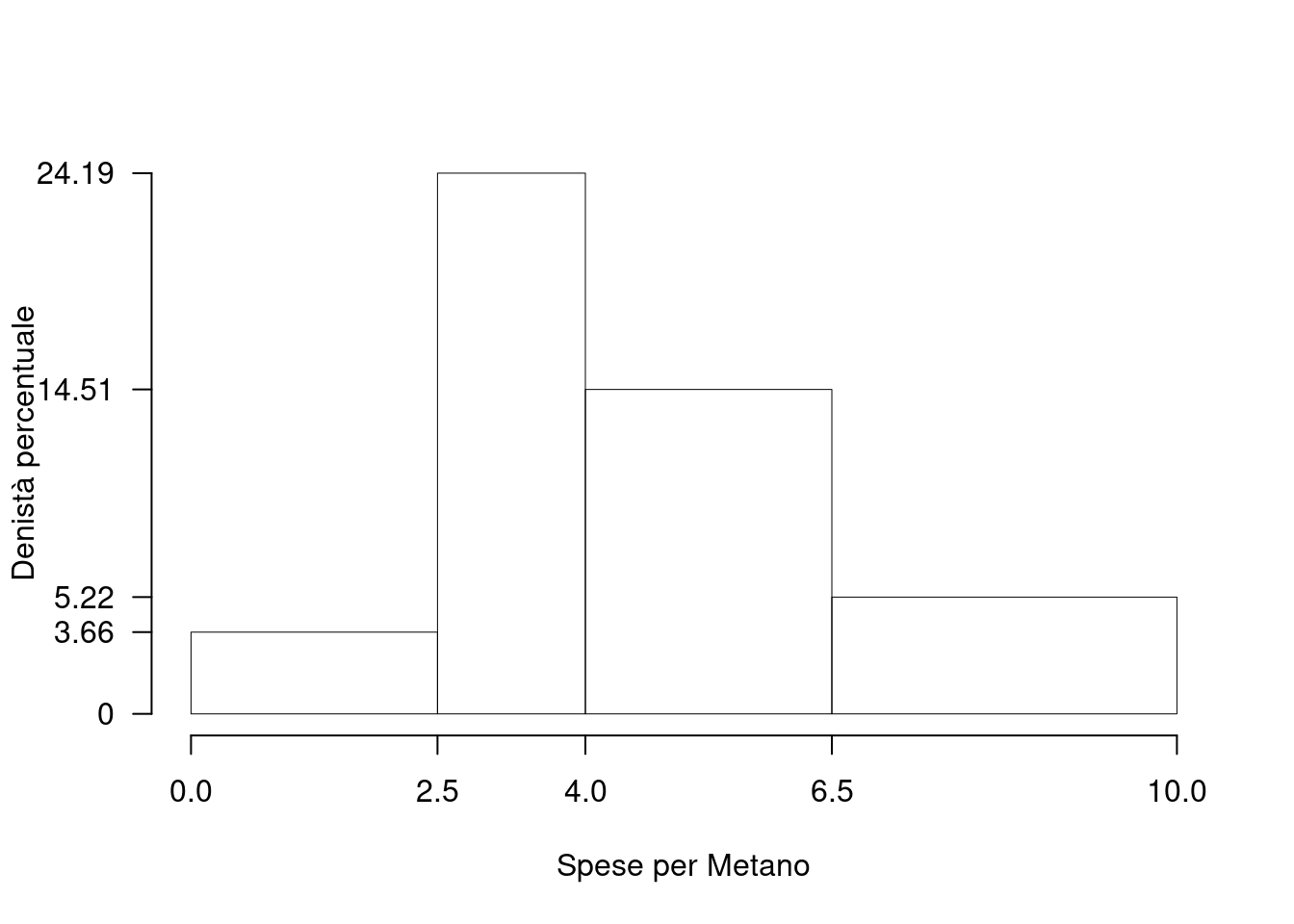
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(h_j\) |
|---|---|---|
| 0.0 | 2.5 | 3.657 |
| 2.5 | 4.0 | 24.191 |
| 4.0 | 6.5 | 14.514 |
| 6.5 | 10.0 | 5.224 |
1.a (Punti 14) Calcolare il valore approssimato della mediana.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(h_j\) | \(b_j\) | \(f_j\) | \(F_j\) |
|---|---|---|---|---|---|
| 0.0 | 2.5 | 3.657 | 2.5 | 0.0914 | 0.0914 |
| 2.5 | 4.0 | 24.191 | 1.5 | 0.3629 | 0.4543 |
| 4.0 | 6.5 | 14.514 | 2.5 | 0.3629 | 0.8171 |
| 6.5 | 10.0 | 5.224 | 3.5 | 0.1829 | 1.0000 |
| 10.0 | 1.0000 |
e quindi:
\[\begin{eqnarray*} p &=& 0.5, \text{essendo }F_{3}=0.8171 >0.5 \Rightarrow j_{0.5}=3\\ x_{0.5} &=& x_{\text{inf};3} + \frac{ {0.5} - F_{2}} {f_{3}} \cdot b_{3} \\ &=& 4 + \frac {{0.5} - 0.4543} {0.3629} \cdot 2.5 \\ &=& 4.315 \end{eqnarray*}\]
1.b (Punti 3) Che relazione dobbiamo aspettarci tra media e mediana?
L’istogramma presenta una coda lunga a sinistra e quindi \[ \bar x > x_{0.5} \]
1.c (Punti 2) La varianza dei dati è pari a \(\sigma^2=4.8382\). Nell’ipotesi che i costi per metano aumentassero del 10%, quanto varrebbe la varianza?
Si tratta di una trasformazione lineare \[ Y = 1.1\cdot X \] e quindi \[ \sigma_Y^2=(1.1)^2\sigma_X^2=5.8542. \]
Esercizio 2
In una stazione ci sono 3 binari. Ogni ora il numero di persone che transita su ogni binario è descritto da una Poisson. In particolare
- \(X_1\sim\text{Pois}(1.1)\), il binario uno;
- \(X_2\sim\text{Pois}(1.1)\), il binario due;
- \(X_3\sim\text{Pois}(0.5)\), il binario tre.
Il numero di persone in transito su un binario è indipendente dal numero di persone in transito sugli altri binari.
2.a (Punti 14) Calcolare la probabilità che il totale delle persone in transito nella stazione, in una data ora, sia maggiore o uguale a due.
Il totale di persone in transito è la somma delle tre Poisson \[ X=X_1+X_2+X_3\sim \text{Pois}(\lambda=1.1+1.1+0.3) \]
\[\begin{eqnarray*} P( X \geq 2 ) &=& 1-P( X < 2 ) \\ &=& 1-\left( \frac{ 2.5 ^{ 0 }}{ 0 !}e^{- 2.5 }+\frac{ 2.5 ^{ 1 }}{ 1 !}e^{- 2.5 } \right)\\ &=& 1-( 0.0821+0.2052 )\\ &=& 1- 0.2873 \\ &=& 0.7127 \end{eqnarray*}\]
2.b (Punti 3) Calcolare la probabilità di osservare una persona su un binario, una persona su un altro binario e nessuna persona sul rimanetene.
Anzitutto osserviamo:
\[\begin{eqnarray*} P(X_1= 0) &=& P(X_2=0)\\ &=& \frac{1.1^0}{0!}e^{-1.1}\\ &=& 0.3329\\ P(X_1= 1) &=& P(X_2=1)\\ &=& \frac{1.1^1}{1!}e^{-1.1}\\ &=& 0.3662\\ P(X_3= 0) &=& \frac{0.5^0}{0!}e^{-0.5}\\ &=& 0.6065\\ P(X_3= 1) &=& \frac{0.5^1}{1!}e^{-0.5}\\ &=& 0.3033\\ \end{eqnarray*}\]
L’evento una persona su un binario, una persona su un altro binario e nessuna persona sul rimanetene si scompone:
\[\begin{eqnarray*} E &=& \big\{(X_1=1\cap X_2=1\cap X_3=0)\cup\\ &&\cup(X_1=1\cap X_2=0\cap X_3=1)\cup\\ &&\cup(X_1=0\cap X_2=1\cap X_3=1)\big\}\\ P(E) &=& \phantom{+} P(X_1=1\cap X_2=1\cap X_3=0)+\\ && + P(X_1=1\cap X_2=0\cap X_3=1)+\\ && + P(X_1=0\cap X_2=1\cap X_3=1)\\ &=& \phantom{+} P(X_1=1)P(X_2=1)P(X_3=0)+\\ && + P(X_1=1)P(X_2=0)P(X_3=1)+\\ && + P(X_1=0)P(X_2=1)P(X_3=1)\\ &=& \phantom{+} 0.3662\cdot0.3662\cdot0.6065+\\ && +0.3662\cdot0.3329\cdot0.3033+\\ && +0.3329\cdot0.3662\cdot0.3033\\ &=& 0.1552 \end{eqnarray*}\]
2.c (Punti 3) Siano \(X_1,...,X_n\), \(n\) VC IID, tali che \[ X_i\sim N(0,1). \] Posto \[ \bar X = \frac{X_1+...+X_n}{n}, \] come si distribuisce \(\bar X\)?
\[ \bar X = \frac{X_1+...+X_n}{n}\sim N\left(0,\frac 1n\right), \]
2.d (Punti 2) Siano \(X_1\sim \text{Binom}(5,0.3)\) e \(X_2\sim \text{Binom}(3,0.3)\). Come si distribuisce, \[X_1+X_2\sim ~~?\]
\[X_1+X_2\sim \text{Binom}(8,0.3)\]
se e solo se \(X_1\) e \(X_2\) sono indipendenti.
Esercizio 3
(Punti 14) Un’urna contiene 4 palline numerate \[\fbox{-1},\fbox{0},\fbox{2},\fbox{3}\] Si estrae \(n=64\) volte con reintroduzione.
Calcolare la probabilità che la media delle 64 estrazioni sia compresa tra 0.92 e 4.08.
\[\begin{eqnarray*} \mu &=& E(X_i) = \sum_{x\in S_X}x P(X=x)\\ &=& ( -1 ) \frac { 1 }{ 4 }+ 0 \frac { 1 }{ 4 }+ 2 \frac { 1 }{ 4 }+ 3 \frac { 1 }{ 4 } \\ &=& 1 \\ \sigma^2 &=& V(X_i) = \sum_{x\in S_X}x^2 P(X=x)-\mu^2\\ &=&\left( ( -1 ) ^2\frac { 1 }{ 4 }+ 0 ^2\frac { 1 }{ 4 }+ 2 ^2\frac { 1 }{ 4 }+ 3 ^2\frac { 1 }{ 4 } \right)-( 1 )^2\\ &=& 2.5 \end{eqnarray*}\]
In virtù del TLC per la media otteniamo
Teorema del Limite Centrale (media VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=64\) VC IID, tc \(E(X_i)=\mu=1\) e \(V(X_i)=\sigma^2=2.5,\forall i\), posto: \[ \bar X=\frac{S_n}n =\frac{X_1 + ... + X_n}n \] allora:\[\begin{eqnarray*} \bar X & \mathop{\sim}\limits_{a}& N(\mu,\sigma^2/n) \\ &\sim & N\left(1,\frac{2.5}{64}\right) \\ &\sim & N(1,0.03906) \end{eqnarray*}\]
\[\begin{eqnarray*} P(0.92<\bar X\leq 4.08) &=& P\left( \frac {0.92 - 1}{\sqrt{0.0391}} < \frac {\bar X - \mu}{\sqrt{\sigma^2/n}} \leq \frac {4.08 - 1}{\sqrt{0.0391}}\right) \\ &=& P\left( -0.4 < Z \leq 15.58\right) \\ &=& \Phi(15.58)-\Phi(-0.4)\\ &=& \Phi( 15.58 )-(1-\Phi( 0.4 )) \\ &=& 1 -(1- 0.6554 ) \\ &=& 0.6554 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Se \(h\) è uno stimatore tale che la sua distorsione va a zero per \(n\) che tende all’infinito: \[ \lim_{n\to \infty}B(h)=0 \] di quale proprietà gode \(h\)?
Osserviamo che \[\begin{align*} B(h) &= E(h)-\theta&\text{e quindi}\\ \lim_{n\to\infty}B(h)&=0\\ \lim_{n\to\infty}(E(h)-\theta)&=0 &\text{se e solo se}\\ \lim_{n\to\infty}E(h)&=\theta &\text{cioè $h$ è asintoticamente corretto} \end{align*}\]
4.b (Punti 3) Definire la funzione di verosimiglianza della Bernoulli.
La verosimiglianza è \[\begin{eqnarray*} L(\pi) &\propto& \prod_{i=1}^n \pi^{x_i}(1-\pi)^{1-x_i}\\ &=& \pi^{s_n}(1-\pi)^{n-s_n}, \qquad s_n=\sum_{i=1}^n x_i \end{eqnarray*}\]
4.c (Punti 3) Un dado, che non sappiamo se è perfetto oppure no, viene lanciato 40 volte. Posto \(\pi_i\) la probabilità che il dado mostri la faccia \(i\), \(i=1,...,6\), si è testato \[ \begin{cases} H_0:\pi_1=\pi_2=...=\pi_6=\frac 16 \end{cases} \] ed è risultato \(p_\text{value}=0.21\). Possiamo concludere che il dado sia truccato?
Il \(p_\text{value}=0.21>0.05\) non c’è motivo per rifiutare \(H_0\), quindi il dado non è truccato.
Esercizio 5
Una casa farmaceutica sta sperimentando un farmaco che lenisce il mal di testa in modo rapido. Osservati \(n=15\) individui, si è registrato che il farmaco agisce in media \(\bar x=26.2\) minuti, con una sd corretta pari a \(S=0.9\).
5.a (Punti 10) Costruire un intervallo di confidenza al 99% per il tempo medio di azione.
\[ S =\sqrt{\frac {n}{n-1}}\cdot\hat\sigma = \sqrt{\frac { 15 }{ 14 }}\cdot 0.9 = 0.9316 \] \[\begin{eqnarray*} Idc: & & \hat\mu \pm t_{n-1;\alpha/2} \times \frac{S}{\sqrt{n}} \\ & & 26.2 \pm 2.977 \times \frac{ 0.9316 }{\sqrt{ 15 }} \\ & & 26.2 \pm 2.977 \times 0.2405 \\ & & [ 25.48 , 26.92 ] \end{eqnarray*}\]
5.b (Punti 4) È ben noto, da studi pregressi, che quella tipologia di farmaci ha un tempo medio di azione pari a 29.3. Testare al livello di significatività dell’1% che il farmaco in sperimentazione agisca in modo uguale agli altri contro l’alternativa che abbia tempi di azione inferiori.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\mu=\mu_0=29.3\text{}\\ H_1:\mu< \mu_0=29.3\text{} \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(T\) \(\sigma^{2}\) di \(\cal{P}\) non è nota: \(\Rightarrow\) t-Test. \[\begin{eqnarray*} S &=& \sqrt{\frac{n} {n-1}}\ \widehat{\sigma} = \sqrt{\frac{15} {15-1}} \times 0.9 = 0.9316 \end{eqnarray*}\]
\[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {S/\,\sqrt{n}}&\sim&t_{n-1}\\ t_{\text{obs}} &=& \frac{ (26.2- 29.3)} {0.9316/\sqrt{15}} = -12.8879\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(t_{(15-1);\, 0.01} = -2.6245\). \[t_{\text{obs}} = -12.8879 < t_{14;\, 0.01} = -2.6245\] CONCLUSIONE: i dati non sono coerenti con \(H_{0}\) al LdS del 1%
Graficamente
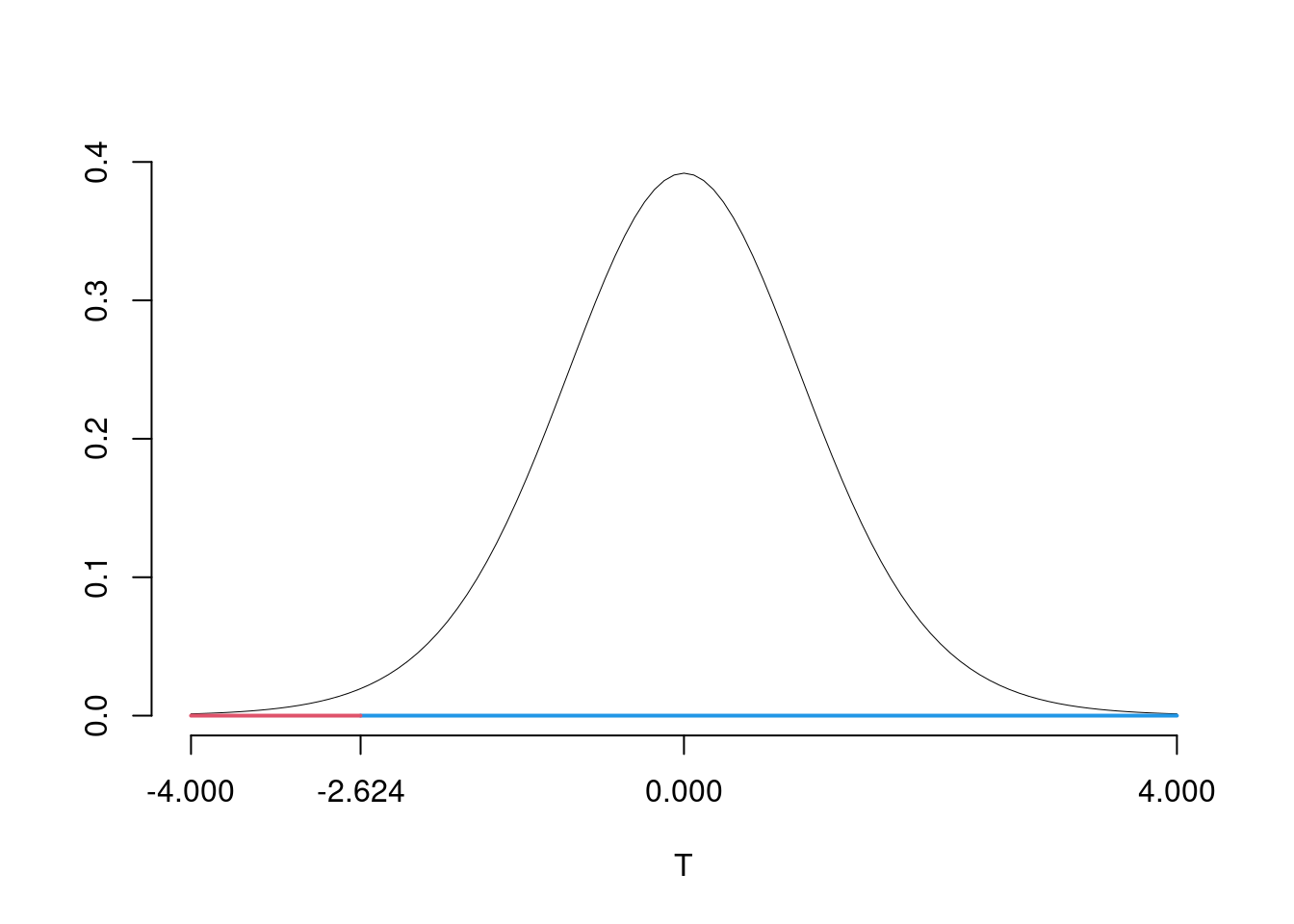
Il \(p_{\text{value}}\) è \[P(T_{n-1}<t_{\text{obs}})=P(T_{n-1}< -12.888 )= 0.000000001861\]
Esercizio 6
In uno studio sul risparmio gestito sono stati intervistati \(n=15\) individui sui quali è stato rilevato il reddito mensile \(X\) (in migliaia di euro), e il risparmio gestito \(Y\) (in migliaia di euro). Il modello di regressione. Qui di seguito i dati e le statistiche di interesse:
| \(i\) | \(x_i\) | \(y_i\) | \(x_i^2\) | \(y_i^2\) | \(x_i\cdot y_i\) |
|---|---|---|---|---|---|
| 1 | 0.470 | 0.0400 | 0.22 | 0.0000 | 0.020 |
| 2 | 1.980 | 0.1600 | 3.92 | 0.0300 | 0.320 |
| 3 | 2.270 | 0.0400 | 5.15 | 0.0000 | 0.090 |
| 4 | 2.380 | 0.0600 | 5.66 | 0.0000 | 0.140 |
| 5 | 2.830 | 0.0600 | 8.01 | 0.0000 | 0.170 |
| 6 | 3.240 | 0.1200 | 10.50 | 0.0100 | 0.390 |
| 7 | 3.960 | 0.1600 | 15.68 | 0.0300 | 0.630 |
| 8 | 4.390 | 0.1400 | 19.27 | 0.0200 | 0.610 |
| 9 | 4.450 | 0.2800 | 19.80 | 0.0800 | 1.250 |
| 10 | 5.750 | 0.2500 | 33.06 | 0.0600 | 1.440 |
| 11 | 7.180 | 0.4000 | 51.55 | 0.1600 | 2.870 |
| 12 | 7.490 | 0.4100 | 56.10 | 0.1700 | 3.070 |
| 13 | 8.480 | 0.5600 | 71.91 | 0.3100 | 4.750 |
| 14 | 8.850 | 0.5600 | 78.32 | 0.3100 | 4.960 |
| 15 | 9.990 | 0.7600 | 99.80 | 0.5800 | 7.590 |
| Totale | 73.710 | 4.0000 | 478.95 | 1.7600 | 28.300 |
| Totale/n | 4.914 | 0.2667 | 31.93 | 0.1173 | 1.887 |
6.a (Punti 14) Stimare il modello di regressione dove il risparmio è funzione del reddito e quello in cui il reddito è funzione del risparmio.
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{15} 73.71= 4.914\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{15} 4= 0.2667\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{15} 478.97 -4.914^2=7.7839\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{15} 1.77 -0.2667^2=0.0469\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{15} 28.3-4.914\cdot0.2667=0.5762\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{0.5762}{7.7839} = 0.074\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 0.2667-0.074\times 4.914=-0.0971 \end{eqnarray*}\]
\[\begin{eqnarray*} \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{15} 4= 0.2667\\ \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{15} 73.71= 4.914\\ \hat\sigma_y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{15} 1.77 -0.2667^2=0.0469\\ \hat\sigma_x^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{15} 478.97 -4.914^2=7.7839\\ \text{cov}(y,x)&=&\frac 1 n\sum_{i=1}^n y_i~x_i-\bar y\bar x=\frac {1}{15} 28.3-0.2667\cdot4.914=0.5762\\ \hat\alpha_1 &=& \frac{\text{cov}(y,x)}{\hat\sigma_y^2} \\ &=& \frac{0.5762}{0.0469} = 0.074\\ \hat\alpha_0 &=& \bar x - \hat\alpha_1 \bar y\\ &=& 4.914-0.074\times 0.2667=-0.0971 \end{eqnarray*}\]
6.b (Punti 3) I due modelli si adattano bene ai dati?
\[ r^2=(0.9538)^2=0.9098>0.75 \]
Sì, i modelli si adattano bene
6.c (Punti 3) Discutere il diagramma dei residui del modello di regressione dove \(Y\) viene spiegata da \(X\).
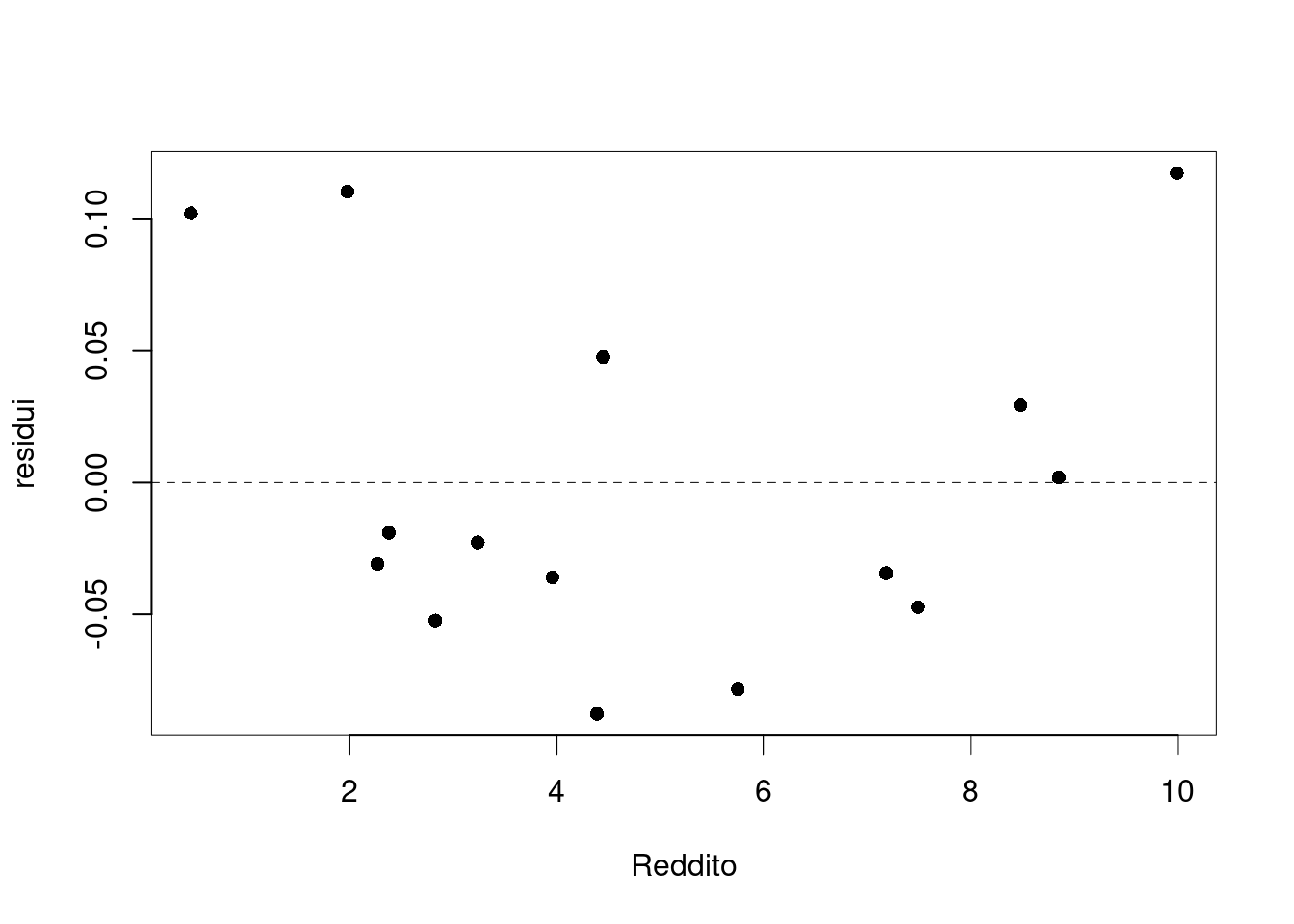
C’è una non linearità evidente, l’assunto zero non è rispettato
6.d (Punti 2) Se ogni individuo risparmiasse 10€ in più al mese, quanto varrebbe \(r\)?
Se ogni individuo risparmiasse 10€ in più al mese allora \[ W=Y+10 \] e in virtù dell’invarianza del coefficiente di correlazione alle trasformazioni lineari otterremmo: \[ r_{XW}=r_{XY}=0.9538 \]
Prova di Statistica 2021/07/22-2
Esercizio 1
Su un campione di \(350\) aziende è stato rilevato il costo annuo in gas metano (espresso in migliaia di euro). Qui di seguito i dati e le frequenze percentuali
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) |
|---|---|---|
| 0.0 | 2.5 | 9.143 |
| 2.5 | 4.0 | 36.286 |
| 4.0 | 6.5 | 36.286 |
| 6.5 | 10.0 | 18.286 |
1.a (Punti 14) Calcolare la colonna delle densità percentuali.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) |
|---|---|---|---|---|---|
| 0.0 | 2.5 | 32 | 0.0914 | 2.5 | 3.657 |
| 2.5 | 4.0 | 127 | 0.3629 | 1.5 | 24.191 |
| 4.0 | 6.5 | 127 | 0.3629 | 2.5 | 14.514 |
| 6.5 | 10.0 | 64 | 0.1829 | 3.5 | 5.224 |
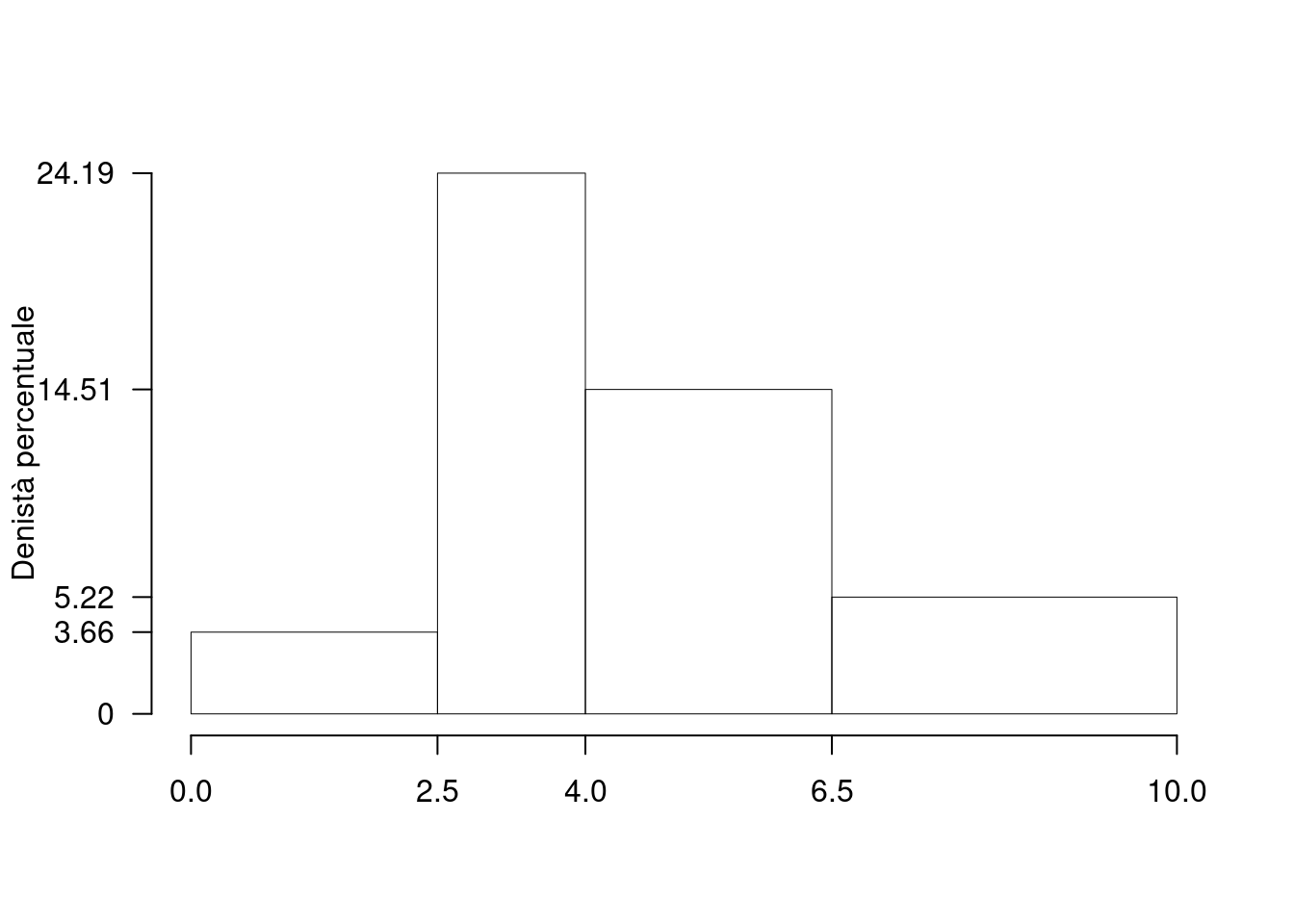
1.b (Punti 3) Calcolare il numero approssimato di aziende con consumo di gas inferiore al 25-esimo percentile \(x_{0.25}\).
Per definizione \[ \%(X\le x_{0.25})=25\% \] \(n=350\) e quindi il 25% di 350 è \[ 350\times0.25=87.5 \]
1.c (Punti 2) È vero che la media aritmetica minimizza la somma dei valori assoluti degli scarti? Perché?
È la mediana che minimizza la somma dei valori assoluti degli scarti. Siccome media e mediana, in generale non coincidono allora no, la media non minimizza la somma dei valori assoluti degli scarti.
Esercizio 2
Ci sono due urne:
- l’urna \(A\): \(\left\{\fbox{0},\fbox{0},\fbox{1}\right\}\) e
- l’urna \(B\): \(\left\{\fbox{0},\fbox{1},\fbox{1}\right\}\).
Si estrae dalle due urne e si somma,
- se la somma fa 2 si vince,
- altrimenti si perde,
poi si rimettono le palline nelle urne e si ripete il gioco per \(n=5\) volte.
2.a (Punti 14) Qual è la probabilità di vincere almeno 1 volta su 5 giocate?
\[ \pi=P(X_A+X_B=2)=P(X_A=1)P(X_B=1)=\frac 13\times\frac23=\frac29=0.2222 \]
\(X\sim\text{Binom}(n=5,\pi=0.2222)\) e quindi
\[\begin{eqnarray*} P( X \geq 1 ) &=& 1-P( X < 1 ) \\ &=& 1-\left( \binom{ 5 }{ 0 } 0.2222 ^{ 0 }(1- 0.2222 )^{ 5 - 0 } \right)\\ &=& 1-( 0.2847 )\\ &=& 1- 0.2847 \\ &=& 0.7153 \end{eqnarray*}\]
2.b (Punti 3) Per giocare si devono puntare due euro ad ogni giocata. Se vinciamo ci vengono dati 9€, i 2€ giocati più 7€ di vincita. Quindi:
- se la somma non fa 2 perdiamo 2€
- se la somma fa 2 riceviamo 9€ (7€ vinti + 2€ giocati)
Quale è il valore atteso della variabile causale che conta il totale di euro ottenuti dopo 5 partite?
Sia \(X_i\) la VC che dice se alla giocata \(i\) si è vinto o perso \[ X_i\sim\text{Ber}\left(\pi=\frac 29\right) \] sia \(Y\) il guadagno/perdita della giocata \(i\) \[ Y_i=-2+9X_i \] e quindi \[ E(Y_i)=E(-2+9X)=-2+9E(X)=-2+9~\frac29=0 \] Sia \(Y\) la vincita totale dopo 5 partite
\[\begin{eqnarray*} Y &=&Y_1+...+Y_5\\ E(Y) &=&E(Y_1+...+Y_5)\\ &=&E(Y_1)+...+E(Y_n)\\ &=& 0+...+0\\ &=& 0 \end{eqnarray*}\]
2.c (Punti 3) Se \(A\) e \(B\) sono due eventi tali che, \(P(A)=0.5\), \(P(B)=0.4\) e \(P(A\cup B)=0.58\). \(A\) e \(B\) sono indipendenti? Perché?
No, perché se lo fossero \[ P(A\cap B)=0.5\times 0.4=0.2 \] e quindi \[\begin{eqnarray*} P(A\cup B) &=& P(A)+P(B)-P(A\cap B)\\ &=& 0.5+0.4-0.2\\ &=& 0.7\ne 0.58 \end{eqnarray*}\]
2.d (Punti 2) Siano \(Y_1,...,Y_n\), \(n\) VA IID, tali che, \(Y_i\sim\chi_{1}^2\), posto \[ X=\sum_{i=1}^n Y_i \] come si distribuisce \(X\)?
Esercizio 3
(Punti 14) Un’urna contiene 150 di palline numerate.
- 40 palline numerate con -1
- 70 palline numerate con 0
- 40 palline numerate con +1
Si estrae \(n=81\) volte con reintroduzione, qual è la probabilità che la somma delle 81 estrazioni sia compresa tra \(-6.6\) e \(+6.6\)?
\[\begin{eqnarray*} \mu &=& E(X_i) = \sum_{x\in S_X}x P(X=x)\\ &=& ( -1 ) \frac { 40 }{ 150 }+ 0 \frac { 70 }{ 150 }+ 1 \frac { 40 }{ 150 } \\ &=& 0 \\ \sigma^2 &=& V(X_i) = \sum_{x\in S_X}x^2 P(X=x)-\mu^2\\ &=&\left( ( -1 ) ^2\frac { 40 }{ 150 }+ 0 ^2\frac { 70 }{ 150 }+ 1 ^2\frac { 40 }{ 150 } \right)-( 0 )^2\\ &=& 0.5333 \end{eqnarray*}\] Teorema del Limite Centrale (somma VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=81\) VC IID, tc \(E(X_i)=\mu=0\) e \(V(X_i)=\sigma^2=0.5333,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\mu,n\sigma^2) \\ &\sim & N(81\cdot0,81\cdot0.5333) \\ &\sim & N(0,43.2) \end{eqnarray*}\]
\[\begin{eqnarray*} P(-6.6<S_n\leq 6.6) &=& P\left( \frac {-6.6 - 0}{\sqrt{43.2}} < \frac {S_n - n\mu}{\sqrt{n\sigma^2}} \leq \frac {6.6 - 0}{\sqrt{43.2}}\right) \\ &=& P\left( -1 < Z \leq 1\right) \\ &=& \Phi(1)-\Phi(-1)\\ &=& \Phi( 1 )-(1-\Phi( 1 )) \\ &=& 0.8413 -(1- 0.8413 ) \\ &=& 0.6826 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(\hat\sigma^2\) lo stimatore di massima verosimiglianza per il parametro \(\sigma^2\) della normale. \(\hat\sigma^2\) è corretto? Quanto vale la sua distorsione?
No, \(\hat\sigma^2\) non è corretto \[ E(\hat\sigma^2)=\frac{n-1}n\sigma^2 \] e quindi \[ B(\hat\sigma^2)=|E(\hat\sigma^2)-\sigma^2|=\frac {\sigma^2}n \]
4.b (Punti 3) Descrivere la tavola della verità di un test.
4.c (Punti 3) In uno studio clinico si è osservato l’effeto sul numero di anticorpi su due gruppi trattati con un farmaco differente. Si è osservato \(\hat\mu_1=10.2\), \(\hat\sigma_1=1.12\) e \(\hat\mu_2=15.6\), \(\hat\sigma_2=3.72\). Posto a test \[ \begin{cases} H_0:\sigma_1=\sigma_2\\ H_1:\sigma_1\ne \sigma_2 \end{cases} \] è risultato \(p_\text{value}=0.21\). Quale test dovremmo usare per testare la differenza tra le medie?
Esercizio 5
Un’azienda automobilistica sta sperimentando un nuovo tipo di motore per ridurre i consumi di carburante. Il motore montato su un’auto prototipo che è stata fatta guidare a \(n=15\) giornalisti. Si è osservato un consumo medio pari \(\bar x=24.5~\text{Km/litro}\) con una deviazione standard \(\hat\sigma=2.25~\text{Km/litro}\).
5.a (Punti 10) Costruire un intervallo di confidenza al 95% per il consumo medio.
\[ S =\sqrt{\frac {n}{n-1}}\cdot\hat\sigma = \sqrt{\frac { 15 }{ 14 }}\cdot 2.25 = 2.329 \] \[\begin{eqnarray*} Idc: & & \hat\mu \pm t_{n-1;\alpha/2} \times \frac{S}{\sqrt{n}} \\ & & 24.5 \pm 2.145 \times \frac{ 2.329 }{\sqrt{ 15 }} \\ & & 24.5 \pm 2.145 \times 0.6013 \\ & & [ 23.21 , 25.79 ] \end{eqnarray*}\]
5.b (Punti 4) È noto che quella fascia di motori ha un consuo medio pari \(23.9~\text{Km/litro}\). Testare al livello di significatività dell’5% che il nuovo motore consumi come gli altri contro l’alternativa che abbia consumi diversi.
\[ \begin{cases} H_0:\mu=23.9\\ H_1:\mu\ne23.9 \end{cases} \]
Siccome \(23.9\notin IdC_{95\%}\) allora rifiuto \(H_0\) al lds del \(5\%\).
Esercizio 6
In uno studio sugli effetti dell’attività sportiva sul benessere delle persone su \(n=25\) atleti si è misurato:
- il numero medio di ore giornaliere passate a correre (\(X\)),
- il numero medio di ore giornaliere passate a fare palestra (\(W\)),
- un indice di stress misurato misurato su opportuna scala (\(Y\)).
qui di seguito le statistiche di interesse
\[\begin{align*} \bar x&=1.1 &\hat \sigma_X&=0.23, \\ \bar w&=0.9 &\hat \sigma_W&=0.12,\\ \bar y&=12.1 &\hat \sigma_Y&=1.17,\\ \text{cov}(X,W)&=-0.021 &\text{cov}(X,Y)&=0.218 \\ &&\text{cov}(W,Y)&=-0.0197 \end{align*}\]
6.a (Punti 14) Stimare il modello di regressione dove l’indice di stress (\(Y\)) è spiegato da \(X\) e quello dove \(Y\) è spiegato da \(W\).
\[\begin{align*} Y_i &= \beta_0+\beta_1 x_i +\varepsilon_i&Y_i &=\gamma_0+\gamma_1W_i\\ \hat\beta_1&=\frac{0.218}{0.23^2} &\hat\gamma_1&=\frac{-0.0323}{0.12^2}\\ &=4.1204 &&=-2.2425\\ \hat\beta_0&=12.1-4.1204\cdot1.1 &\hat\beta_0&=12.1-(-2.2425\cdot0.9)\\ &=7.5675 &&=14.1182\\ r_{XY}&=\frac{0.218}{0.23\cdot1.17} &r_{WY}&=\frac{-0.0323}{0.12\cdot1.17}\\ &=0.81 &&=-0.23\\ \end{align*}\]
6.b (Punti 3) Quale dei due modelli è più affidabile?
\[\begin{align*} R_{XY}^2 &= 0.81^2 &R_{WY}^2 &= -0.23^2 \\ &=0.6561 &&=0.0529 \end{align*}\]
quindi \(X\) spiega \(Y\) meglio di \(W\).
6.c (Punti 3) Considerata la scomposizine della TSS di \(X\) rispetto ad \(Y\). \[ TSS = ESS + RSS \] quanto vale il rapporto \[ \frac{ESS}{TSS}=~? \]
\[ \frac{ESS}{TSS}=~R_{XY}^2=0.6561 \]
6.d (Punti 2) Sotto ipotesi di normalità dei residui, come sono distribuiti gli stimatori dei mini quadrati \(\hat\beta_0\) e \(\hat\beta_1\)?
\[\begin{eqnarray*} \hat\beta_1&\sim& N\left(\beta_1, \frac{\sigma_{\varepsilon}^{2}} {n \hat{\sigma}^{2}_{X}} \right)\\ \hat\beta_0&\sim& N\left(\beta_0, \sigma_{\varepsilon}^{2} \left( \frac{1} {n} + \frac{\bar{x}^{2}} {n \hat{\sigma}^{2}_{X}} \right) \right) \end{eqnarray*}\]
Prova di Statistica 2021/09/06-1
Esercizio 1
Su un campione di \(155\) aziende è bilancio annuo (espresso in migliaia di euro). Qui di seguito la distribuzione delle frequenze percentuali:| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) |
|---|---|---|
| -10 | -5 | 3.871 |
| -5 | 0 | 40.645 |
| 0 | 3 | 36.774 |
| 3 | 20 | 18.710 |
| 100.000 |
1.a (Punti 14) Individuare la classe modale.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|---|
| -10 | -5 | 3.871 | 6 | 0.0387 | 5 | 0.7742 | 0.0387 |
| -5 | 0 | 40.645 | 63 | 0.4065 | 5 | 8.1290 | 0.4452 |
| 0 | 3 | 36.774 | 57 | 0.3677 | 3 | 12.2581 | 0.8129 |
| 3 | 20 | 18.710 | 29 | 0.1871 | 17 | 1.1006 | 1.0000 |
| 100.000 | 155 | 1.0000 | 30 |
1.b (Punti 3) Quante aziende, approssimativamente, hanno un bilancio inferiore a 1.5?
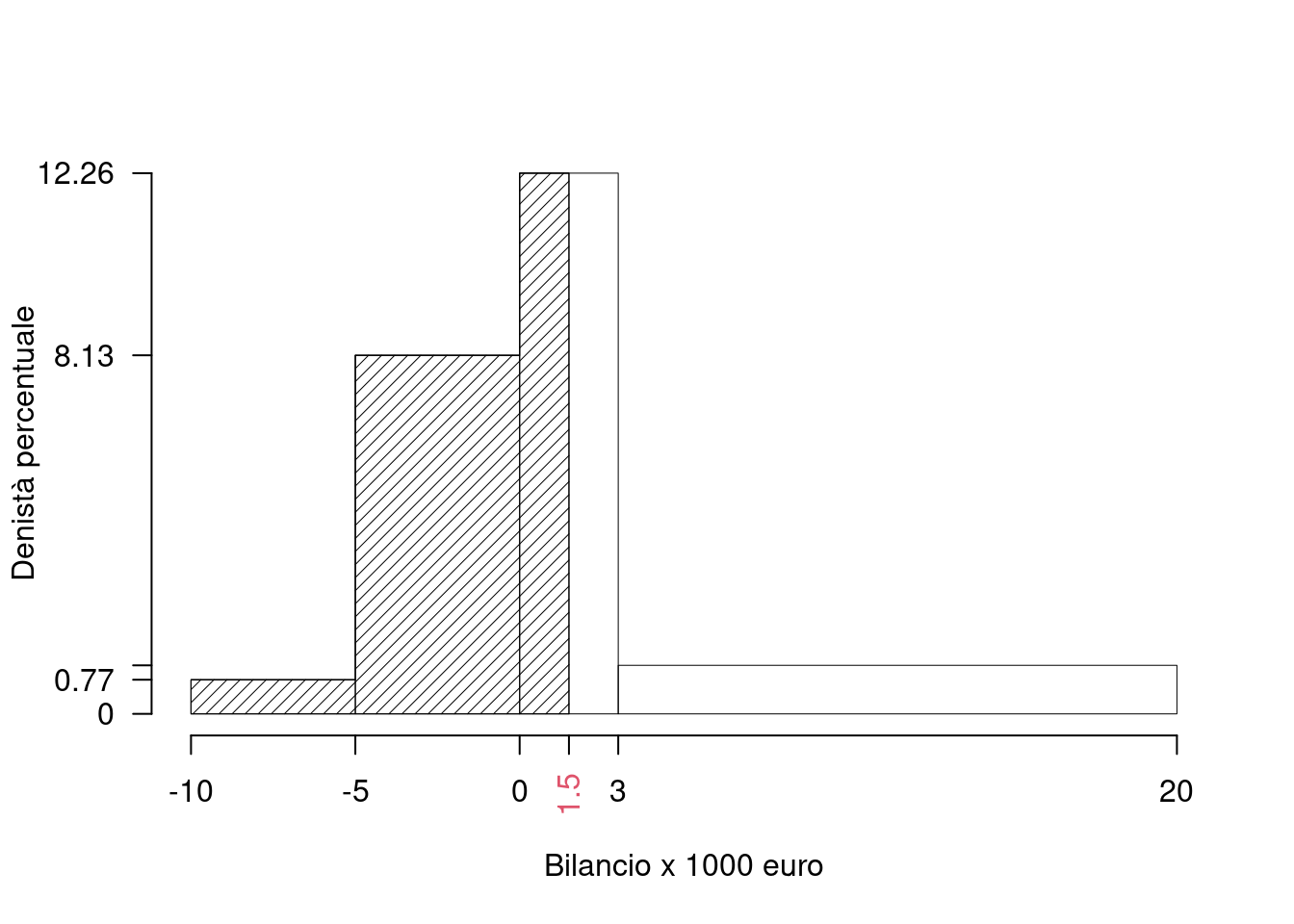 \[\begin{eqnarray*}
\%(X< 1.5 ) &=& f_{ 1 }\times 100+f_{ 2 }\times 100 +( 1.5 - 0 )\times h_{ 3 } \\
&=& ( 0.0387 )\times 100+( 0.4065 )\times 100 +( 1.5 )\times 12.26 \\
&=& 0.629 \times(100) \\
\#(X< 1.5 ) &=& 97.5
\end{eqnarray*}\]
\[\begin{eqnarray*}
\%(X< 1.5 ) &=& f_{ 1 }\times 100+f_{ 2 }\times 100 +( 1.5 - 0 )\times h_{ 3 } \\
&=& ( 0.0387 )\times 100+( 0.4065 )\times 100 +( 1.5 )\times 12.26 \\
&=& 0.629 \times(100) \\
\#(X< 1.5 ) &=& 97.5
\end{eqnarray*}\]
1.c (Punti 2) Che relazione dobbiamo aspettarci tra media e mediana?
1.d (Punti 2) La varianza dei dati è pari a \(\sigma^2=36.8775\). Nell’ipotesi che tutte le aziende aumentassero il loro bilancio di 10 mila ero, quanto varrebbe la varianza dei così trasformati?
Esercizio 2
Siano \(X_1\sim N(10,2)\) e sia \(X_2\sim N(10,3)\). Posto \(A=\{X_1<11\}\), \(B=\{X_1>9\}\), e \(C=\{9<X_2<10\}\)
2.a (Punti 14) Quanto vale \(P\Big((A\cap B)\cap C\Big)\)?
\[ (A\cap B)\cap C = \{9<X_1<11\}\cap\{9<X_2<10\} \] e quindi
\[\begin{eqnarray*} P(9<X_1\leq 11) &=& P\left( \frac {9 - 10}{\sqrt{2}} < \frac {X_1 - \mu_1}{\sigma_1} \leq \frac {11 - 10}{\sqrt{2}}\right) \\ &=& P\left( -0.71 < Z \leq 0.71\right) \\ &=& \Phi(0.71)-\Phi(-0.71)\\ &=& \Phi( 0.71 )-(1-\Phi( 0.71 )) \\ &=& 0.7611 -(1- 0.7611 ) \\ &=& 0.5222 \end{eqnarray*}\] inoltre
\[\begin{eqnarray*} P(9<X_2\leq 10) &=& P\left( \frac {9 - 10}{\sqrt{3}} < \frac {X_2 - \mu_2}{\sigma_2} \leq \frac {10 - 10}{\sqrt{3}}\right) \\ &=& P\left( -0.58 < Z \leq 0\right) \\ &=& \Phi(0)-\Phi(-0.58)\\ &=& \Phi( 0 )-(1-\Phi( 0.58 )) \\ &=& 0.5 -(1- 0.719 ) \\ &=& 0.219 \end{eqnarray*}\] e infine \[ P\Big(\{9<X_1<11\}\cap\{9<X_2<10\}\Big)=P\Big(\{9<X_1<11\}\Big)P\Big(\{9<X_2<10\}\Big)= 0.1135 \]
2.b (Punti 3) Posto \(Y=X_1-X_2\), calcolare \(P(Y<-1)\).
\[Y=X_1-X_2\sim N(10-10,2+3)\]
\[\begin{eqnarray*} P(Y < -1) &=& P\left( \frac {Y - \mu_Y}{\sigma_Y} < \frac {-1 - 0}{\sqrt{5}} \right) \\ &=& P\left( Z < -0.45\right) \\ &=& 1-\Phi( 0.45 ) \\ &=& 0.3264 \end{eqnarray*}\]
2.c (Punti 3) Siano \(X_1,...,X_n\), \(n\) VC IID, tali che \(X_i\sim \text{Ber}(\pi)\), posto \[ X = X_1+...+X_n \] come si distribuisce \(X\)?
2.d (Punti 2) Sia \(X\sim \text{Pois}(1.5)\), per quali valori \(x\), \(F(x)\), la funzione di ripartizione di \(X\) è minore o uguale a 0.5? Ovvero, per quali \(x\) la seguente è rispettata \(F(x)\le 0.5\)?
Per definizione \[\begin{eqnarray*} F(x) &=& P(X\le x)\\ &=&\sum_{t=0}^x f(t)\\ &=&\sum_{t=0}^x \frac{\lambda^t}{t!}e^{-\lambda}\\ \end{eqnarray*}\]
\[\begin{eqnarray*} F(0) &=& \frac{1.5^0}{0!}e^{-1.5}=0.2231\\ F(1) &=& \frac{1.5^0}{0!}e^{-1.5}+ \frac{1.5^1}{1!}e^{-1.5}=0.5578 \end{eqnarray*}\]
Esercizio 3
3.a (Punti 2) Enunciare il teorema centrale del limite per la somma.
3.b (Punti 14) Il numero di incidenti giornalieri sul lavoro del comparto \(A\) è distribuito come una Poisson di parametro \(\lambda = 0.1\). In un anno \(n=365\) quale è la probabilità che il numero totale di incidenti sia minore di 40?
\(E(X_i)=0.1\), \(V(X_i)=0.1\) e quindi Teorema del Limite Centrale (somma VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=365\) VC IID, tc \(E(X_i)=\mu=36.5\) e \(V(X_i)=\sigma^2=36.5,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\mu,n\sigma^2) \\ &\sim & N(365\cdot36.5,365\cdot36.5) \\ &\sim & N(13322,13322) \end{eqnarray*}\]
\[\begin{eqnarray*} P(S_n < 40) &=& P\left( \frac {S_n - n\mu}{\sqrt{n\sigma^2}} < \frac {40 - 13322.5}{\sqrt{13322.5}} \right) \\ &=& P\left( Z < -115.08\right) \\ &=& 1-\Phi( 115.08 ) \\ &=& 0 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Siano \(h_1\) e \(h_2\) due stimatori corretti per \(\theta\), cosa significa che \(h_1\) è più efficiente di \(h_2\)?
4.b (Punti 3) Definire la funzione di verosimiglianza della Poisson.
4.c (Punti 3) Una moneta, che non sappiamo se è perfetta oppure no, viene lanciata 40 volte. Posto \(\pi\) la probabilità che la moneta mostri testa, si è testato \[ \begin{cases} H_0:\pi=\frac 12\\ H_1:\pi\ne\frac 12 \end{cases} \] ed è risultato \(p_\text{value}=0.021\). Possiamo concludere che la moneta sia truccata?
4.d (Punti 2) In caso di campionamento casuale semplice senza reintroduzione quanto vale la varianza della media aritmetica campionaria?
Siano \(X_1,...,X_m\) \(n\) VC estratte senza reintroduzione allora \[\begin{eqnarray*} E(\bar X) &=& \mu\\ V(\bar X) &=& \frac{N-n}{N-1}\frac{\sigma^2}{n} \end{eqnarray*}\]
Esercizio 5
Si sono intervistate 16 piccole imprese modenesi. L’analisi ha mostrato che sentono una forte necessità di investimenti nell’ambito della ricerca industriale; tuttavia, l’importo medio annuale speso per la ricerca industriale è risultato pari a 2750.00€ con una deviazione standard pari a 1300.00€.
5.a (Punti 7) Determinare un intervallo di confidenza al 95% per l’importo medio annuale speso per la ricerca industriale.
\[ S =\sqrt{\frac {n}{n-1}}\cdot\hat\sigma = \sqrt{\frac { 16 }{ 15 }}\cdot 1300 = 1342.6342 \] \[\begin{eqnarray*} Idc: & & \hat\mu \pm t_{n-1;\alpha/2} \times \frac{S}{\sqrt{n}} \\ & & 2750 \pm 2.131 \times \frac{ 1342.6342 }{\sqrt{ 16 }} \\ & & 2750 \pm 2.131 \times 335.7 \\ & & [ 2035 , 3465 ] \end{eqnarray*}\]
5.b (Punti 7) Una indagine più vasta dell’anno precedente ha fornito una spesa media per la ricerca industriale pari a 3250.00€ con una deviazione standard pari a 1200.00€. Al livello di significatività del 5%, verificare l’ipotesi che l’importo medio nell’ultimo anno sia stato equivalente a quello dell’anno precedente contro l’alternativa di una diminuzione dell’investimento in ricerca industriale.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\mu=\mu_0=3250\text{}\\ H_1:\mu< \mu_0=3250\text{} \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\) \(\sigma^{2}\) di \(\cal{P}\) è nota: \(\Rightarrow\) z-Test. \[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {\sigma/\sqrt{n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ (2750- 3250)} {1200/\sqrt{16}} = -1.6667\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(z_{0.05} = -1.6449\). \[z_{\text{obs}} = -1.6667 < z_{0.05} = -1.6449\]
CONCLUSIONE: i dati non sono coerenti con \(H_{0}\) al LdS del 5%
Graficamente
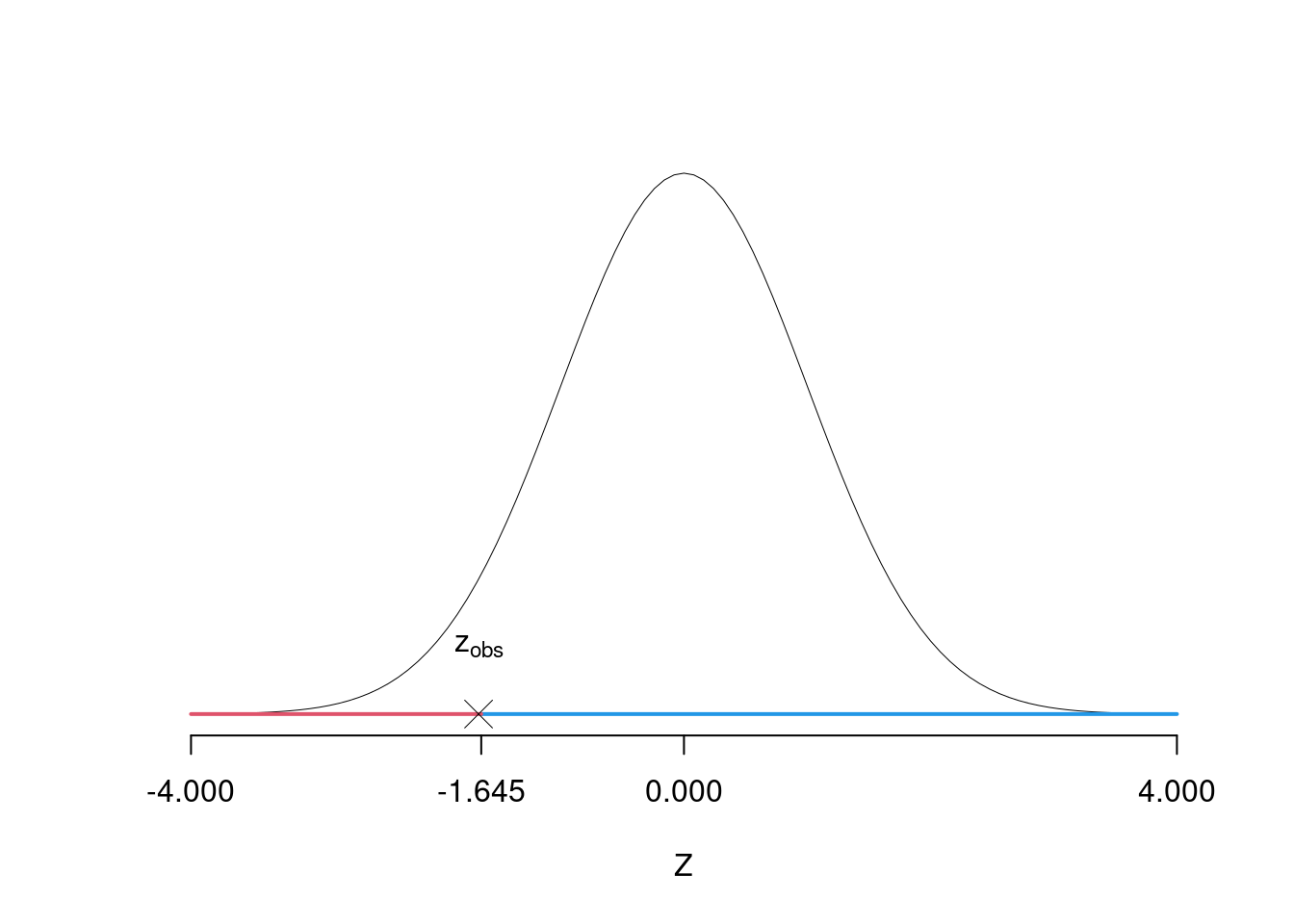
Il \(p_{\text{value}}\) è \[P(Z<z_{\text{obs}})=P(Z< -1.67 )= 0.04779\]
Esercizio 6
Si esaminano \(n=15\) aziende e si rileva, per ognuna di esse, il fatturato (\(X\)) e il profitto (\(Y\)) (in unità convenzionali). Si osservano le seguenti statistiche, \(\sum_{i=1}^{15}x_i=73.71\), \(\sum_{i=1}^{15}y_i=4\), \(\sum_{i=1}^{15}x_i^2=478.9693\), \(\sum_{i=1}^{15}y_i^2=1.7694\) e \(\sum_{i=1}^{15}x_iy_i=28.2996\).
6.a (Punti 14) Stimare il modello di regressione dove \(Y\) viene spiegata da \(X\)
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{15} 74= 4.9333\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{15} 4= 0.2667\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{15} 479 -4.9333^2=7.5956\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{15} 2 -0.2667^2=0.0622\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{15} 28-4.9333\cdot0.2667=0.5711\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{0.5711}{7.5956} = 0.0752\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 0.2667-0.0752\times 4.9333=-0.1043 \end{eqnarray*}\]
6.b (Punti 3) Qual è la percentuale di varianza spiegata dal modello?
\[\begin{eqnarray*} r&=&\frac{\text{cov}(X,Y)}{\sigma_X\sigma_Y}=\frac{ 0.5711 }{ 2.756 \times 0.2494 }= 0.8307 \\r^2&=& 0.6901 < 0.75 \end{eqnarray*}\] Il modello non si adatta bene ai dati.
6.c (Punti 2) Se in un modello di regressione si conoscono \(\hat\beta_1\), \(r^2\) e \(\hat\sigma_X\) è possibile ricavare \(\hat\sigma_Y\)? In che modo?
\[\begin{eqnarray*} \hat\beta_1 &=& \frac{\text{cov}(x,y)}{\hat\sigma_X^2}\\ \text{cov}(x,y)&=&\hat\beta_1\hat\sigma_X^2\\ r&=&\frac{\text{cov}(x,y)}{\hat\sigma_X\hat\sigma_Y}\\ \hat\sigma_Y&=&\frac{\text{cov}(x,y)}{r\hat\sigma_X}\\ &=&\frac{\hat\beta_1\hat\sigma_X^2}{r\hat\sigma_X}\\ &=&\frac{\hat\beta_1}{r}\hat\sigma_X \end{eqnarray*}\]
6.d (Punti 2) Cosa significa che il coefficiente di correlazione è invariante alle trasformazioni lineari?