Esercizi su Test e Intervalli di Confidenza

t-Test a due campioni

In uno studio sull’efficacia della pubblicità si è proceduto facendo vedere lo spot \(A\) ad un campione di 10 individui (gruppo \(A\)) e lo spot \(B\) ad un secondo campione di 20 individui (gruppo \(B\)). Si è quindi misurato il gradimento con opportuna scala. Il gradimento medio del gruppo \(A\) risulta pari a 95 con una deviazione standard pari a 5.4 mentre il gradimento medio del gruppo \(B\) risulta pari a 92 con una deviazione standard pari a 5.9. Verificare l’ipotesi, al livello di significatività dell’1%, che il gradimento medio dei due spot sia uguale, contro l’alternativa che lo spot \(A\) sia mediamente più gradito di quello \(B\). Si assuma l’ipotesi di eterogeneità delle varianze dei due gruppi, anche se i numeri non sembrano giustificarla.

\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI

\[\begin{cases} H_0:\mu_\text{A} = \mu_\text{ B}\text{}\\ H_1:\mu_\text{A} > \mu_\text{ B}\text{} \end{cases}\]

\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(T\)

L’ipotesi è di eterogeneità e quindi calcoliamo: \[ S^2_\text{A}=\frac{n_\text{A}}{n_\text{A}-1}\hat\sigma^2_\text{A}=\frac{10}{10-1}5.4^2=32.4 \qquad S^2_\text{B}=\frac{n_\text{B}}{n_\text{B}-1}\hat\sigma^2_\text{B}=\frac{20}{20-1}5.9^2=36.6421 \]

\[\begin{eqnarray*} \frac{\hat\mu_\text{A} - \hat\mu_\text{B}} {\sqrt{\frac {S^2_\text{A}}{n_\text{A}}+\frac {S^2_\text{B}}{n_\text{B}}}}&\sim&t_{n_\text{A}+n_\text{B}-2}\\ t_{\text{obs}} &=& \frac{ (95- 92)} {\sqrt{\frac{32.4}{10}+\frac{36.6421}{20}}} = 1.3321\, . \end{eqnarray*}\]

\(\fbox{C}\) DECISIONE

Dalle tavole si ha \(t_{(10+20-2);\, 0.01} = 2.4671\). \[t_{\text{obs}} = 1.3321 < t_{28;\, 0.01} = 2.4671\]

CONCLUSIONE: i dati sono coerenti con \(H_{0}\) al LdS del 1%

Graficamente

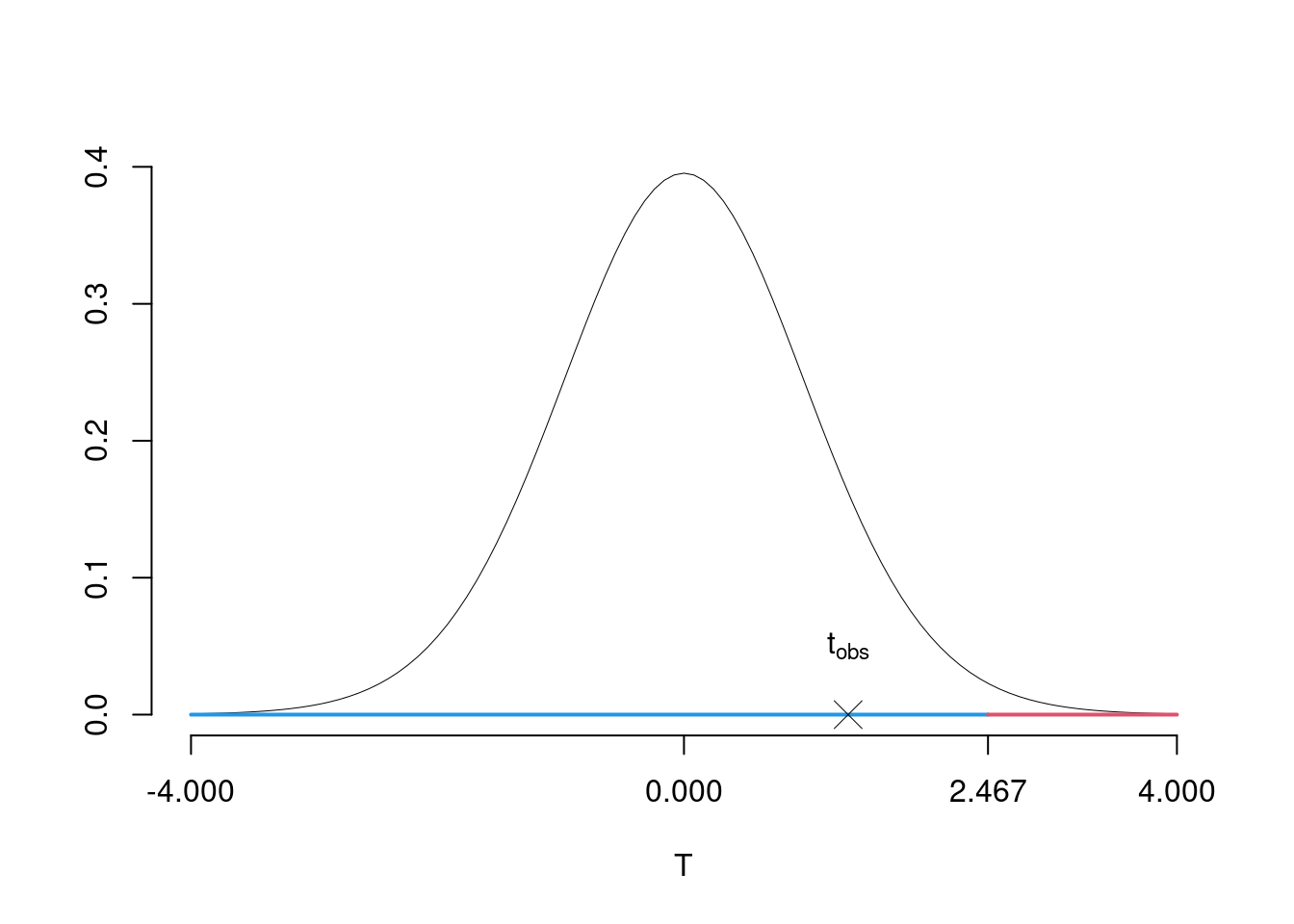
Il \(p_{\text{value}}\) è \[P(T_{n1+n2-2}>t_{\text{obs}})=P(T_{n1+n2-2}> 1.332 )= 0.09679\]

Un campione: IdC e z-test

Un’indagine in 17 aziende, che producono lo stesso prodotto, ha rilevato che il costo per unità è pari a euro 30.00 in media con una deviazione standard pari a euro 1.50.

Determinare un intervallo di confidenza al 99% per il costo medio per unità.

\[ S =\sqrt{\frac {n}{n-1}}\cdot\hat\sigma = \sqrt{\frac { 17 }{ 16 }}\cdot 1.546 = 1.5938 \] \[\begin{eqnarray*} Idc: & & \hat\mu \pm t_{n-1;\alpha/2} \times \frac{ S }{\sqrt{n}} \\ & & 30 \pm 2.921 \times \frac{ 1.5462 }{\sqrt{ 17 }} \\ & & 30 \pm 2.921 \times 0.3865 \\ & & [ 28.87 , 31.13 ] \end{eqnarray*}\]

L’indagine dell’anno precedente, condotta su un campione molto pi'u numeroso, mostrava un costo medio pari a euro 29.00 con una deviazione standard pari a 2.00 euro. Verificare l’ipotesi che il costo medio del prodotto osservato nell’anno corrente sia equivalente a quello osservato nell’anno precedente contro l’alternativa di un aumento del costo. Specificare in modo esplicito il tipo di test utilizzato, l’ipotesi nulla e l’ipotesi alternativa e trarre le opportune conclusioni.

\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\mu=\mu_0=29\text{}\\ H_1:\mu> \mu_0=29\text{} \end{cases}\]

\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\) \(\sigma^{2}\) di \(\cal{P}\) è nota: \(\Rightarrow\) z-Test. \[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {\sigma/\sqrt{n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ (30- 29)} {2/\sqrt{17}} = 2.0616\, . \end{eqnarray*}\]

\(\fbox{C}\) DECISIONE Dalle tavole si ha \(z_{0.05} = 1.6449\). \[z_{\text{obs}} = 2.0616 > z_{0.05} = 1.6449\]

CONCLUSIONE: i dati non sono coerenti con \(H_{0}\) al LdS del 5%

Graficamente

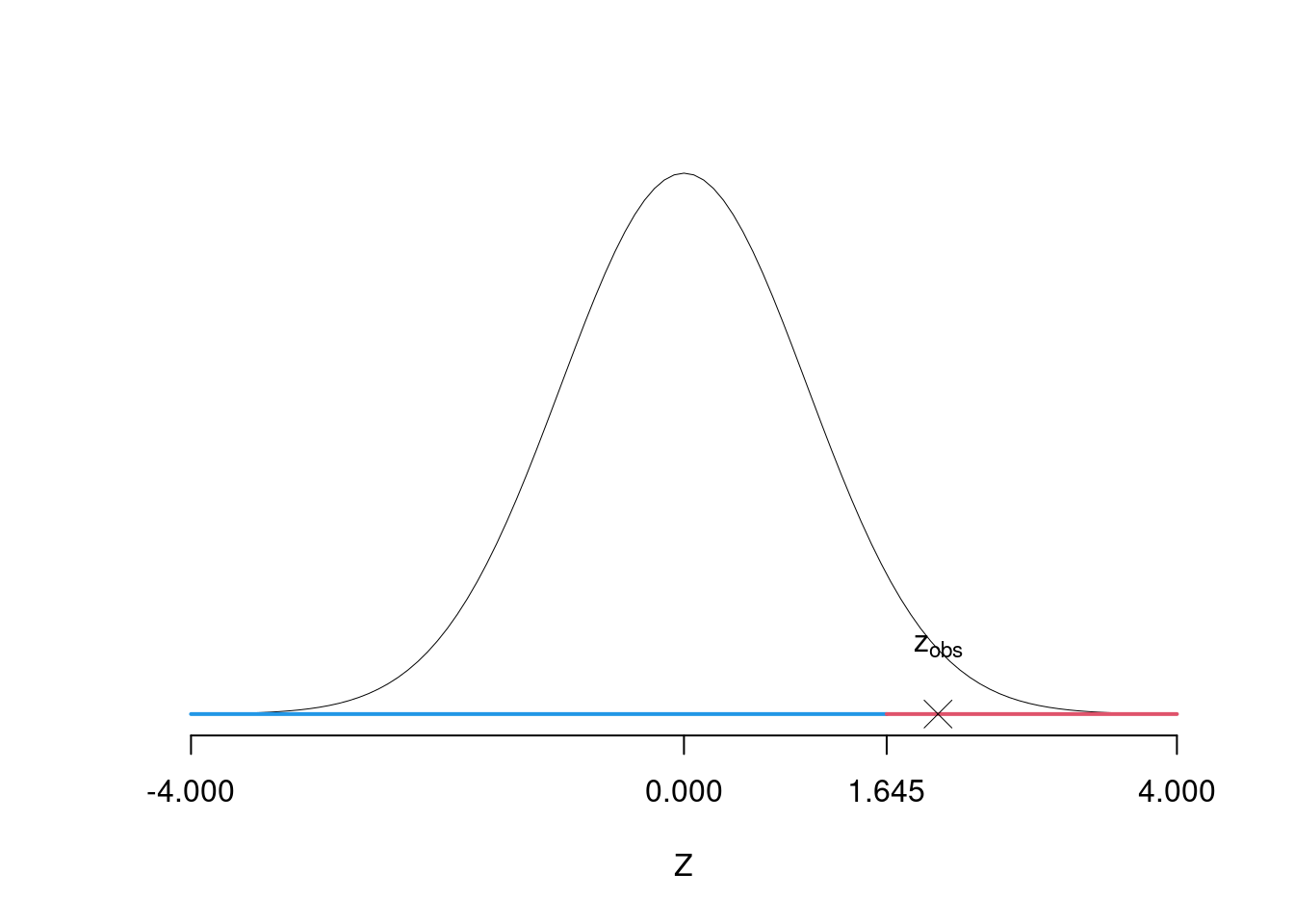
Il \(p_{\text{value}}\) è \[P(Z>z_{\text{obs}})=P(Z> 2.06 )= 0.01963\]

Un campione: IdC e t-test

Sia \(X\) l’età dei parlamentari italiani. Si sceglie un campione di 20 parlamentari italiani e si ottiene una media di 48.5 anni con una deviazione standard pari a 10.6 anni.

Determinare un intervallo di confidenza al 95% per l’età media dei politici italiani.

\[ S =\sqrt{\frac {n}{n-1}}\cdot\hat\sigma = \sqrt{\frac { 20 }{ 19 }}\cdot 10.88 = 11.1579 \] \[\begin{eqnarray*} Idc: & & \hat\mu \pm t_{n-1;\alpha/2} \times \frac{ S }{\sqrt{n}} \\ & & 48.5 \pm 2.093 \times \frac{ 10.8754 }{\sqrt{ 20 }} \\ & & 48.5 \pm 2.093 \times 2.495 \\ & & [ 43.28 , 53.72 ] \end{eqnarray*}\]

è noto che l’età media dei politici europei è di 55 anni. Verificare al livello di significatività dell’1% l’ipotesi che l’età media dei politici italiani sia uguale a quella dei politici europei contro l’alternativa che sia minore.

\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\mu=\mu_0=55\text{}\\ H_1:\mu< \mu_0=55\text{} \end{cases}\]

\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(T\) \(\sigma^{2}\) di \(\cal{P}\) non è nota: \(\Rightarrow\) t-Test. \[\begin{eqnarray*} S &=& \sqrt{\frac{n} {n-1}}\ \widehat{\sigma} = \sqrt{\frac{20} {20-1}} \times 10.6 = 10.8754 \end{eqnarray*}\]

\[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {S/\,\sqrt{n}}&\sim&t_{n-1}\\ t_{\text{obs}} &=& \frac{ (48.5- 55)} {10.8754/\sqrt{20}} = -2.6729\, . \end{eqnarray*}\]

\(\fbox{C}\) DECISIONE Dalle tavole si ha \(t_{(20-1);\, 0.01} = -2.5395\). \[t_{\text{obs}} = -2.6729 < t_{19;\, 0.01} = -2.5395\] CONCLUSIONE: i dati non sono coerenti con \(H_{0}\) al LdS del 1%

Graficamente

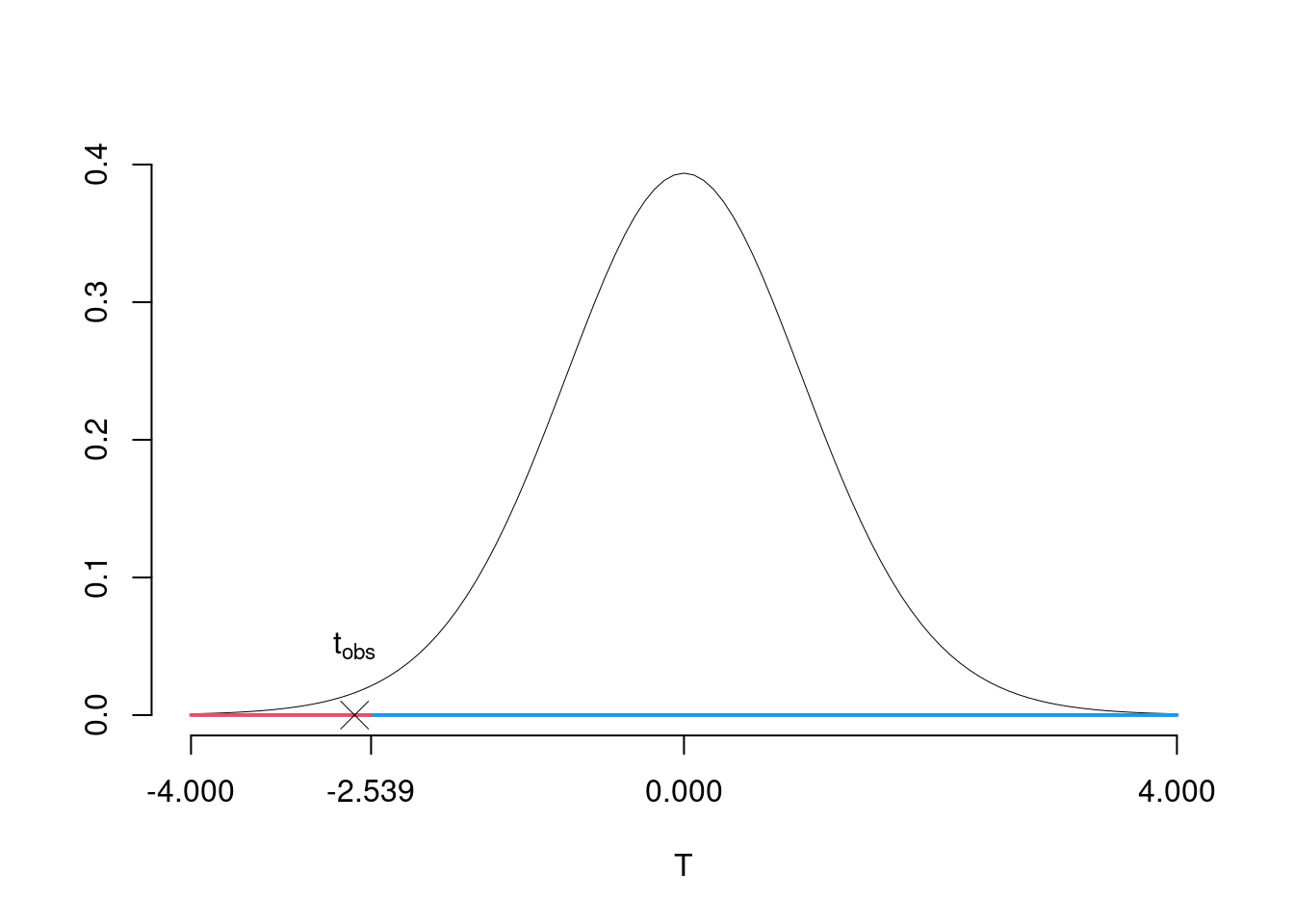
Il \(p_{\text{value}}\) è \[P(T_{n-1}<t_{\text{obs}})=P(T_{n-1}< -2.673 )= 0.007521\]

Un campione: IdC e t-test

Per accertare lo stato di preparazione dei dipendenti di una struttura pubblica si è estratto un campione di 26 impiegati. A ogni impiegato è stato somministrato un test, con punteggio da 0 a 100, per accertare il suo grado di competenza, \(X\). Il valore medio ottenuto è pari a 78 con una deviazione standard pari a 12.

Determinare un intervallo di confidenza al 95% per \(\mu = E(X)\).

\[ S =\sqrt{\frac {n}{n-1}}\cdot\hat\sigma = \sqrt{\frac { 26 }{ 25 }}\cdot 12.24 = 12.48 \] \[\begin{eqnarray*} Idc: & & \hat\mu \pm t_{n-1;\alpha/2} \times \frac{ S }{\sqrt{n}} \\ & & 78 \pm 2.06 \times \frac{ 12.2376 }{\sqrt{ 26 }} \\ & & 78 \pm 2.06 \times 2.448 \\ & & [ 72.96 , 83.04 ] \end{eqnarray*}\]

Si supponga che il punteggio medio del test in un ampio studio sulla popolazione di impiegati, sia pari a 72. Con un livello di significatività uguale a 0.01 si può ritenere che il valore medio osservato nel campione sia diverso da 72?

\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\mu=\mu_0=72\text{}\\ H_1:\mu\neq \mu_0=72\text{} \end{cases}\] Siccome \(H_1\) è bilaterale, considereremo \(\alpha/2\), anziché \(\alpha\)

\[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {S/\,\sqrt{n}}&\sim&t_{n-1}\\ t_{\text{obs}} &=& \frac{ (78- 72)} {12.2376/\sqrt{26}} = 2.5\, . \end{eqnarray*}\]

\(\fbox{C}\) DECISIONE Dalle tavole si ha \(t_{(26-1);\, 0.005} = 2.7874\). \[t_{\text{obs}} = 2.5 < t_{25;\, 0.005} = 2.7874\] CONCLUSIONE: i dati sono coerenti con \(H_{0}\) al LdS del 1%

Graficamente

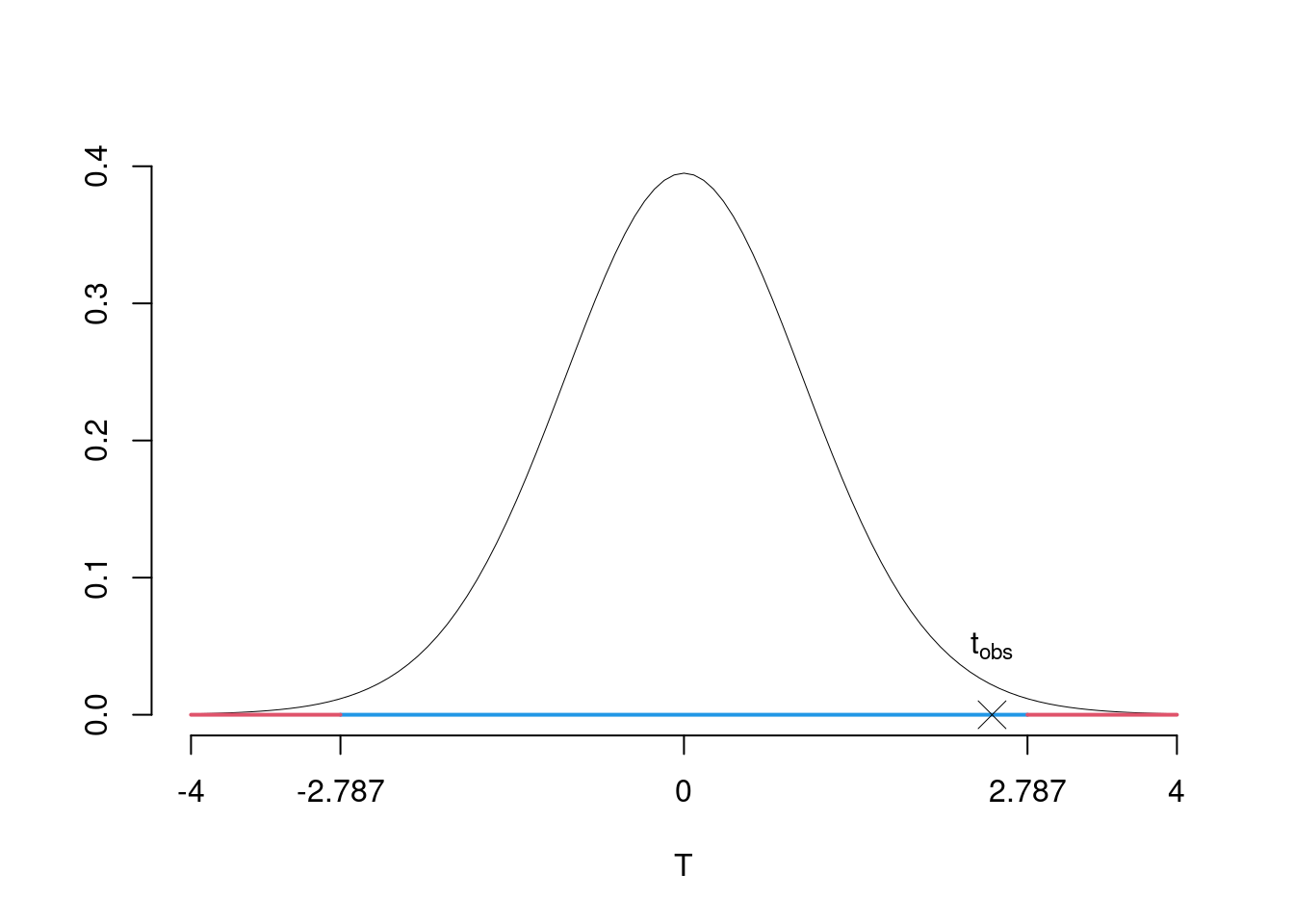
Il \(p_{\text{value}}\) è \[P(|T_{n-1}|>|t_{\text{obs}}|)=2P(T_{n-1}>|t_{\text{obs}}|)=2P(T_{n-1}>| 2.5 |)= 0.01934\]

Due campioni: proporzione

Per verificare se ci sia differenza di genere sulla riforma costituzionale del governo Renzi, si è condotta una indagine su 120 donne e 120 uomini. Dalle interviste è emerso che 60 dei 120 uomini si siano dichiarati favorevoli, mentre 30 delle 120 donne si siano dichiarate favorevoli (numeri di comodo per avere pochi decimali). Verificare, al livello di significatività del 5%, l’ipotesi che non ci sia differenza tra uomini e donne, contro l’alternativa che le donne siano meno favorevoli alla riforma costituzionale. Specificare l’ipotesi nulla e l’ipotesi alternativa, il tipo di test da utilizzare, e le conclusioni.

\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\pi_\text{U} = \pi_\text{ D}\text{}\\ H_1:\pi_\text{U} > \pi_\text{ D}\text{} \end{cases}\]

\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)

\[\hat\pi_\text{U}=\frac{s_\text{U}}{n_\text{U}}=\frac{60}{120}=0.5\qquad \hat\pi_\text{D}=\frac{s_\text{D}}{n_\text{D}}=\frac{30}{120}=0.25\]

Calcoliamo la proporzione comune sotto \(H_0\) \[ \pi_C=\frac{s_\text{U}+s_\text{D}}{n_\text{U}+n_\text{D}}= \frac{90}{240}=0.375 \]

\[\begin{eqnarray*} \frac{\hat\pi_\text{U} - \hat\pi_\text{D}} {\sqrt{\frac {\pi_C(1-\pi_C)}{n_\text{U}}+\frac {\pi_C(1-\pi_C)}{n_\text{D}}}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ (0.5- 0.25)} {\sqrt{\frac{0.375(1-0.375)}{120}+\frac{0.375(1-0.375)}{120}}} = 4\, . \end{eqnarray*}\]

\(\fbox{C}\) DECISIONE Dalle tavole si ha \(z_{0.05} = 1.6449\). \[z_{\text{obs}} = 4 > z_{0.05} = 1.6449\]

CONCLUSIONE: i dati non sono coerenti con \(H_{0}\) al LdS del 5%

Graficamente

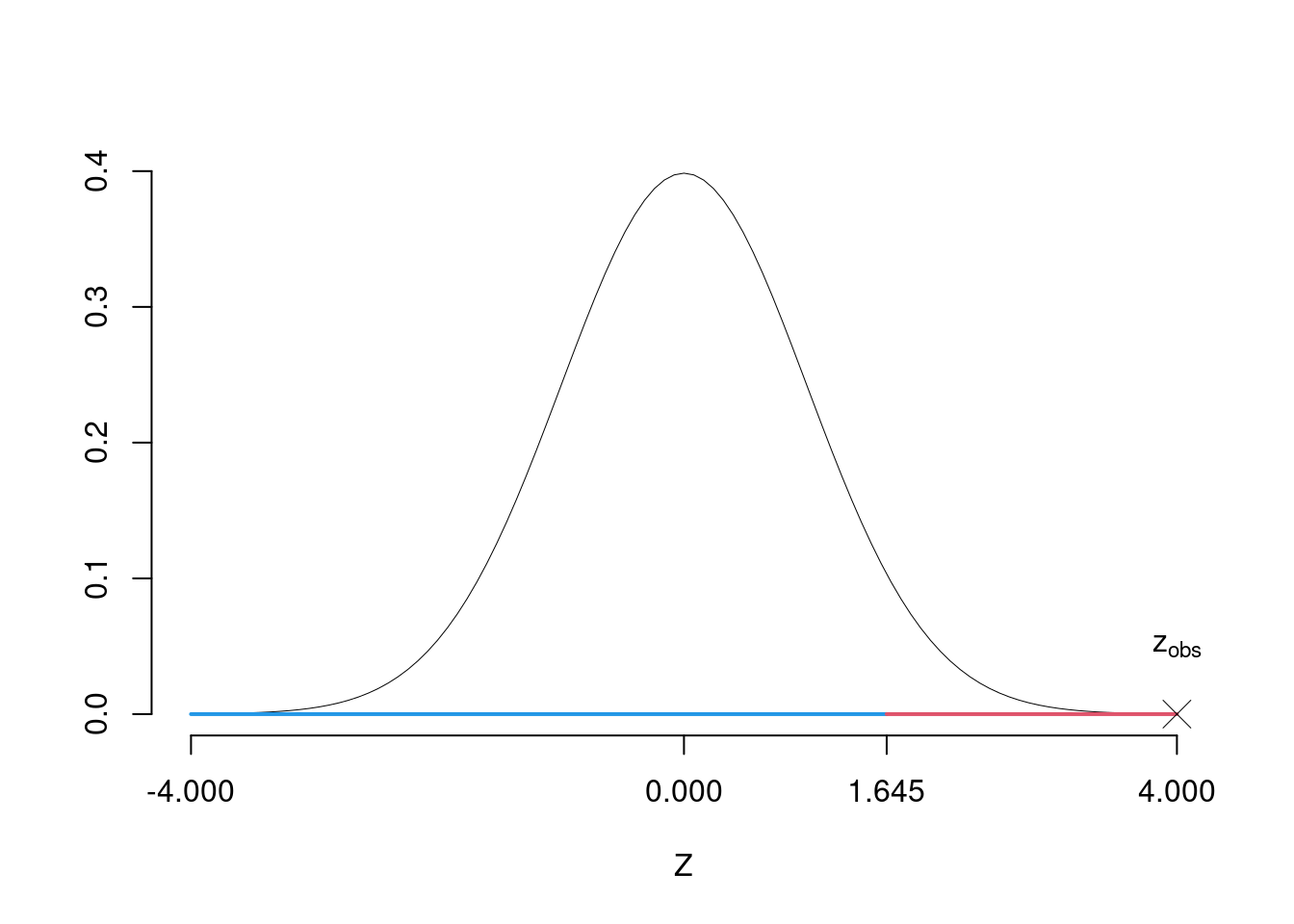
Il \(p_{\text{value}}\) è \[P(Z>z_{\text{obs}})=P(Z> 4 )= 0.00003167\]