Anno 2022
Prova di Statistica 2022/06/16-1
Esercizio 1
Su un campione di \(250\) famiglie della provincia di Ferrara è stato rilevata la spesa in generi alimentari (espresso in migliaia di euro). Qui di seguito la distribuzione delle frequenze cumulate:
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(F_j\) |
|---|---|---|
| 0 | 3 | 0.0683 |
| 3 | 5 | 0.4618 |
| 5 | 10 | 0.8193 |
| 10 | 20 | 1.0000 |
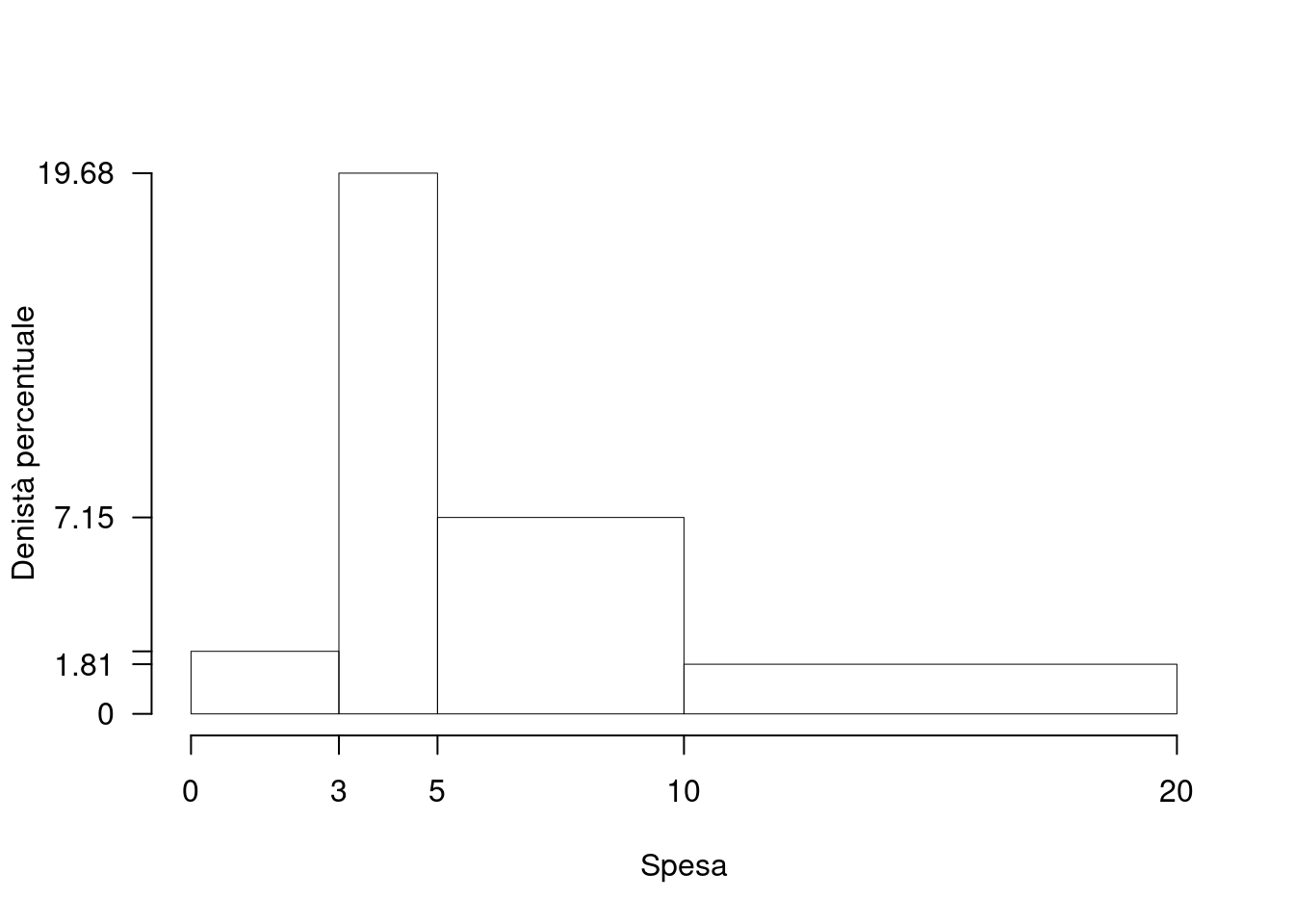
1.a (Punti 14) Disegnare l’istogramma di densità percentuale.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|---|
| 0 | 3 | 6.827 | 17 | 0.0683 | 3 | 2.276 | 0.0683 |
| 3 | 5 | 39.357 | 98 | 0.3936 | 2 | 19.679 | 0.4618 |
| 5 | 10 | 35.743 | 89 | 0.3574 | 5 | 7.149 | 0.8193 |
| 10 | 20 | 18.072 | 45 | 0.1807 | 10 | 1.807 | 1.0000 |
| 100.000 | 249 | 1.0000 | 20 |
1.b (Punti 3) Quante famiglie hanno una spesa superiore al 75-esimo percentile?
\[\%(X>x_{0.75})=25\% , \rightarrow 250\times 0.25=62.5 \]
1.c (Punti 2) Che relazione dobbiamo aspettarci tra media e mediana?
\[ \bar x > x_{0.5} \]
1.d (Punti 2) La spesa media è pari a \(\bar x=7.1245\), mentre la SD è pari a \(SD=4.7792\). Se ogni famiglia aumentasse la spesa di 0.5, quanto varrebbero la media e la SD dei dati?
Invariata
Esercizio 2
Siano \(X\sim N(102,1.5)\) e sia \(Y\sim N(50,3.5)\), \(X\) e \(Y\) indipendenti. Posto \(A=\{X>100\}\), \(B=\{X<102\}\), e \(C=\{47<Y\le 53\}\).
2.a (Punti 14) Quanto vale \(P\Big((A\cap B)\cup C\Big)\)?
\[\begin{eqnarray*} P(100<X\leq 102) &=& P\left( \frac {100 - 102}{\sqrt{1.5}} < \frac {X - \mu_X}{\sigma_X} \leq \frac {102 - 102}{\sqrt{1.5}}\right) \\ &=& P\left( -1.63 < Z \leq 0\right) \\ &=& \Phi(0)-\Phi(-1.63)\\ &=& \Phi( 0 )-(1-\Phi( 1.63 )) \\ &=& 0.5 -(1- 0.9484 ) \\ &=& 0.4484 \end{eqnarray*}\]
\[\begin{eqnarray*} P(47<Y\leq 53) &=& P\left( \frac {47 - 50}{\sqrt{3.5}} < \frac {Y - \mu_Y}{\sigma_Y} \leq \frac {53 - 50}{\sqrt{3.5}}\right) \\ &=& P\left( -1.6 < Z \leq 1.6\right) \\ &=& \Phi(1.6)-\Phi(-1.6)\\ &=& \Phi( 1.6 )-(1-\Phi( 1.6 )) \\ &=& 0.9452 -(1- 0.9452 ) \\ &=& 0.8904 \end{eqnarray*}\]
\[\begin{eqnarray*} P(A\cap B\cup C) &=& P(A\cap B)+P(C)-P(A\cap B\cap C)\\ &=& P(A\cap B)+P(C)-P(A\cap B)P(C)\\ &=& 0.4488+0.8912-0.4488\times0.8912\\ &=& 0.94 \end{eqnarray*}\]
2.b (Punti 3) Si estrae 5 volte da \(X\sim N(102,1.5)\), posto \(A=\{X>100\}\), quale è la probabilità che \(A\) si avveri 3 volte su 5?
\[ \pi=P(A)=0.9088 \]
\[ P(3\text{ su }5)=\binom{5}{3}0.9088^3(1-0.9088)^5=0.0624 \]
2.c (Punti 2) Se \(F\) è la funzione di ripartizione della VA \(X\), posto \(a < b\) due numeri qualunque, a cosa equivale \[ F(b)-F(a) \qquad? \]
\[ F(b)-F(a) = P(a<X\le b) \]
Esercizio 3
3.a (Punti 14) Ogni giorno un impianto di produzione confeziona 1000 lotti. In media il 10 di questi lotti sono fallati, con una deviazione standard pari a 0.3. Dopo 300 giorni di produzione qual è la probabilità che il numero di lotti fallati sia maggiore di 3100?
\(E(X_i)=10\), \(V(X_i)=0.09\) e quindi
Teorema del Limite Centrale (somma VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=300\) VC IID, tc \(E(X_i)=\mu=10\) e \(V(X_i)=\sigma^2=0.09,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\mu,n\sigma^2) \\ &\sim & N(300\cdot10,300\cdot0.09) \\ &\sim & N(3000,27) \end{eqnarray*}\]
\[\begin{eqnarray*} P(S_n > 3100) &=& P\left( \frac {S_n - n\mu}{\sqrt{n\sigma^2}} > \frac {3100 - 3000}{\sqrt{27}} \right) \\ &=& P\left( Z > 19.25\right) \\ &=& 1-P(Z< 19.25 )\\ &=& 1-\Phi( 19.25 ) \\ &=& 0 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(\hat \lambda\) lo stimatore di massima verosimiglianza di \(\lambda\) del modello di Poisson. \[\begin{eqnarray*} \hat\lambda &=& \frac 1n\sum_{i=1}^nx_i\\ \end{eqnarray*}\] Dimostrare le correttezza di \(\hat\lambda\) in almeno tre passaggi.
4.b (Punti 2) Definire lo Standard Error di uno stimatore.
4.c (Punti 3) Definire gli errori di primo e di secondo tipo di un test statistico.
4.d (Punti 3) In un test statistico, per quali valori di \(p_\text{value}\) si tende a rifiutare \(H_0\)?
Esercizio 5
(Punti 14) Il Supermercato \(S\), della catena \(C\), ha monitorato gli accessi al suo interno per una settimana. Qui di seguito il numero di accessi per giorno della settimana di \(S\) e la percentuale di accessi nella catena \(C\).
| Lun | Mart | Merc | Giov | Ven | Tot | |
|---|---|---|---|---|---|---|
| Supermercato S | 59 | 20 | 30 | 24 | 117 | 250 |
| Catena C | 25% | 10% | 10% | 10% | 45% | 100% |
Testare l’ipotesi che nel supermercato \(S\) la distribuzione degli accessi nei giorni della settimana sia uguale a quella della catena.
\(\fbox{A}\) Formulazione delle ipotesi \[ \{H_0:F_S\sim F_\text{Catena} \] \(\fbox{B}\) Scelta e calcolo della statistica test.
Si tratta di un test chi quadro di conformità.| Lun | Mart | Merc | Giov | Ven | Tot | |
|---|---|---|---|---|---|---|
| Supermercato S | 59 | 20 | 30 | 24 | 117 | 250 |
| Catena C | 25% | 10% | 10% | 10% | 45% | 100% |
| \(n_j^*\) | 62.5 | 25 | 25 | 25 | 112.5 | 250 |
| \(\chi^2\) | 0.196 | 1 | 1 | 0.04 | 0.18 | 2.416 |
\(\fbox{C}\) Decisione
Il chi quadro osservato è 4.832 è minore di \(\chi^2_{4;0.05}\) 9.4877, 13.2767, e quindi non rifiuto \(H_0\).
Esercizio 6
In uno studio sul potere d’acquisto delle famiglie è stato selezionato un campione di 150 nuclei familiari a cui è stato chiesto il reddito (\(X\)) e la percezione della perdita del potere d’acquisto espresso su una scala che va da zero a 1 (\(Y\)). Qui di seguito le statistiche bivariate
\[\begin{align*} \sum_{i=1}^n x_i &= 110.55, &\sum_{i=1}^n x_i^2 &= 127.03 \\ \sum_{i=1}^n y_i &= 112.68, &\sum_{i=1}^n y_i^2 &= 86.61 \\ \sum_{i=1}^n x_iy_i &= 74.32. \end{align*}\]
6.a (Punti 14) Stimare la previsione per \(x=1.5\) nel modello di regressione dove \(Y\) viene spiegata da \(X\).
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{150} 110.55= 0.737\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{150} 112.68= 0.7512\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{150} 127.03 -0.737^2=0.09\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{150} 86.61 -0.7512^2=0.0131\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{150} 74.32-0.737\cdot0.7512=-0.0582\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{-0.0582}{0.09} = -0.1915\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 0.7512-(-0.1915)\times 0.737=0.8924 \end{eqnarray*}\]
\[\hat y_{X= 1.5 }=\hat\beta_0+\hat\beta_1 x= 0.8924 + (-0.1915) \times 1.5 = 0.6051 \]
6.b (Punti 3) Qual è la percentuale di varianza spiegata dal modello?
\[\begin{eqnarray*} r&=&\frac{\text{cov}(X,Y)}{\sigma_X\sigma_Y}=\frac{ -0.05817 }{ 0.5511 \times 0.1144 }= -0.9223 \\r^2&=& 0.8506 > 0.75 \end{eqnarray*}\] Il modello si adatta bene ai dati.
6.c (Punti 2) Interpretare i parametri di regressione \(\hat\beta_0\) e \(\hat\beta_1\).
6.d (Punti 2) Se \(W=-10\times Y\), quanto varrà \(r_{XW}\), coefficiente di correlazione tra \(X\) e \(W\)?
\[r_{WX}=-r_{XY}=0.9223\]
Prova di Statistica 2022/06/16-2
Esercizio 1
Su un campione di \(250\) famiglie della provincia di Ferrara è stato rilevata la spesa in generi alimentari (espresso in migliaia di euro). Qui di seguito i dati raccolti in classe e le densità di frequenza percentuali
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(h_j\) |
|---|---|---|
| 0 | 3 | 2.40 |
| 3 | 5 | 19.60 |
| 5 | 10 | 7.12 |
| 10 | 20 | 1.80 |
1.a (Punti 14) Calcolare il valore approssimato della mediana.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|---|
| 0 | 3 | 7.2 | 18 | 0.072 | 3 | 2.40 | 0.072 |
| 3 | 5 | 39.2 | 98 | 0.392 | 2 | 19.60 | 0.464 |
| 5 | 10 | 35.6 | 89 | 0.356 | 5 | 7.12 | 0.820 |
| 10 | 20 | 18.0 | 45 | 0.180 | 10 | 1.80 | 1.000 |
| 100.0 | 250 | 1.000 | 20 |
\[\begin{eqnarray*} p &=& 0.5, \text{essendo }F_{3}=0.82 >0.5 \Rightarrow j_{0.5}=3\\ x_{0.5} &=& x_{\text{inf};3} + \frac{ {0.5} - F_{2}} {f_{3}} \cdot b_{3} \\ &=& 5 + \frac {{0.5} - 0.464} {0.356} \cdot 5 \\ &=& 5.5056 \end{eqnarray*}\]
1.b (Punti 3) Quante famiglie hanno una spesa inferiore al 25-esimo percentile?
\[ 250\times 0.25=62.5 \]
1.c (Punti 2) La spesa media è pari a \(\bar x=6.9973\), che forma ci dobbiamo aspettare dell’istogramma di densità?
1.d (Punti 2) La varianza della spesa è pari a \(Var=18.3466\). Se ogni famiglia aumentasse la sua spesa del 5%, quanto varrebbe varianza dei dati così trasformati?
\[20.2272\]
Esercizio 2
Siano \(X\sim \text{Pois}(1.5)\) e sia \(Y\sim \text{Pois}(1.5)\), \(X\) e \(Y\) indipendenti. Posto \(A=\{X<2\}\) e \(B=\{Y\ge 2\}\)
2.a (Punti 14) Quanto vale \(P(A\cup B)\)?
\[\begin{eqnarray*} P(A) &=& P(X=0)+P(X=1)\\ &=& \frac{1.5^0}{0!}e^{-1.5}+\frac{1.5^1}{1!}e^{-1.5}\\ &=& 0.5578\\ P(B) &=& 1-P(A)\\ &=&0.4422\\ P(A\cup B) &=& P(A)+P(B)-P(A\cap B)\\ &=& 0.7533 \end{eqnarray*}\]
2.b (Punti 3) Si estrae 6 volte da \(X\sim \text{Pois}(1.5)\), posto \(A=\{X<2\}\), quale è la probabilità che \(A\) si avveri 3 volte su 6?
\[\begin{eqnarray*} P(A) &=& P(X=0)+P(X=1)\\ &=& \frac{1.5^0}{0!}e^{-1.5}+\frac{1.5^1}{1!}e^{-1.5}\\ &=& 0.2231+0.3347\\ &=& 0.5578\\ P(\text{3 successi su 6}) &=& \binom{6}{3}0.5578^3(1-0.5578)^{6-3}\\ &=&0.3001 \end{eqnarray*}\]
2.c (Punti 2) Se \(X\) è una VC con valore atteso \(E(X)=0.5\) e \(V(X)=1.2\), posto \(Y=X^2\) è vero che \(E(Y)=E^2(X)\)?
Esercizio 3
3.a (Punti 14) Si lancia un dado perfetto 100 volte. Qual è la probabilità che la proporzione di volte che si osserva la faccia sei (⚅) sia maggiore di 0.2?
Soluzione
\(E(X_i)=0.1667\), \(V(X_i)=0.1389\) e quindi Teorema del Limite Centrale (proporzione)
Siano \(X_1\),…,\(X_n\), \(n=100\) VC IID, tc \(X_i\sim\text{Ber}(\pi=0.1667)\)\(,\forall i\), posto: \[ \hat\pi=\frac{S_n}n = \frac{X_1 + ... + X_n}n \] allora:\[\begin{eqnarray*} \hat\pi & \mathop{\sim}\limits_{a}& N(\pi,\pi(1-\pi)/n) \\ &\sim & N\left(0.1667,\frac{0.1667\cdot(1-0.1667))}{100}\right) \\ &\sim & N(0.1667,0.001389) \end{eqnarray*}\]
\[\begin{eqnarray*} P(\hat\pi > 0.2) &=& P\left( \frac {\hat\pi - \pi}{\sqrt{\pi(1-\pi)/n}} > \frac {0.2 - 0.1667}{\sqrt{0.0014}} \right) \\ &=& P\left( Z > 0.89\right) \\ &=& 1-P(Z< 0.89 )\\ &=& 1-\Phi( 0.89 ) \\ &=& 0.1867 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(\hat \mu\) lo stimatore di massima verosimiglianza di \(\mu\) del modello Normale. \[\begin{eqnarray*} \hat\mu &=& \frac 1n\sum_{i=1}^nx_i\\ \end{eqnarray*}\] Dimostrare le consistenza di \(\hat\mu\) in almeno tre passaggi.
4.b (Punti 2) Siano \(h_1\) e \(h_2\) due stimatori per \(\theta\), cosa significa dire che \(h_1\) è più efficiente di \(h_2\)?
4.c (Punti 3) Definire la significatività e la potenza di un test statistico.
4.d (Punti 3) Se in un test statistico il \(p_\text{value}>0.1\) possiamo rifiutare \(H_0\)?
Esercizio 5
5.a (Punti 12) In un’indagine sull’opinione sul reddito di cittadinanza sono stati intervistate 140 persone che vivono al nord e 170 che vivono al sud: 60 su 140 che vivono al nord sono favorevoli al reddito di cittadinanza mentre 95 su 170 che vivono al sud sono favorevoli.
Testare all’un percento che la proporzione di persone favorevoli al reddito di cittadinanza che vivono al sud sia uguale a quelle di quelli che vivono al nord, contro l’alternativa che siano diverse.
5.b (Punti 2) Calcolare e discutere il \(p\)-value del test precedente.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\pi_\text{N} = \pi_\text{ S}\text{}\\ H_1:\pi_\text{N} \neq \pi_\text{ S}\text{} \end{cases}\] Siccome \(H_1\) è bilaterale, considereremo \(\alpha/2\), anziché \(\alpha\)
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)
\[\hat\pi_\text{N}=\frac{s_\text{N}}{n_\text{N}}=\frac{60}{140}=0.4286\qquad \hat\pi_\text{S}=\frac{s_\text{S}}{n_\text{S}}=\frac{95}{170}=0.5588\]
Calcoliamo la proporzione comune sotto \(H_0\) \[ \pi_C=\frac{s_\text{N}+s_\text{S}}{n_\text{N}+n_\text{S}}= \frac{155}{310}=0.5 \]
\[\begin{eqnarray*} \frac{\hat\pi_\text{N} - \hat\pi_\text{S}} {\sqrt{\frac {\pi_C(1-\pi_C)}{n_\text{N}}+\frac {\pi_C(1-\pi_C)}{n_\text{S}}}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ (0.4286- 0.5588)} {\sqrt{\frac{0.5(1-0.5)}{140}+\frac{0.5(1-0.5)}{170}}} = -2.2826\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(z_{0.005} = -2.5758\). \[z_{\text{obs}} = -2.2826 > z_{0.005} = -2.5758\]
CONCLUSIONE: i dati sono coerenti con \(H_{0}\) al LdS del 1%
Graficamente
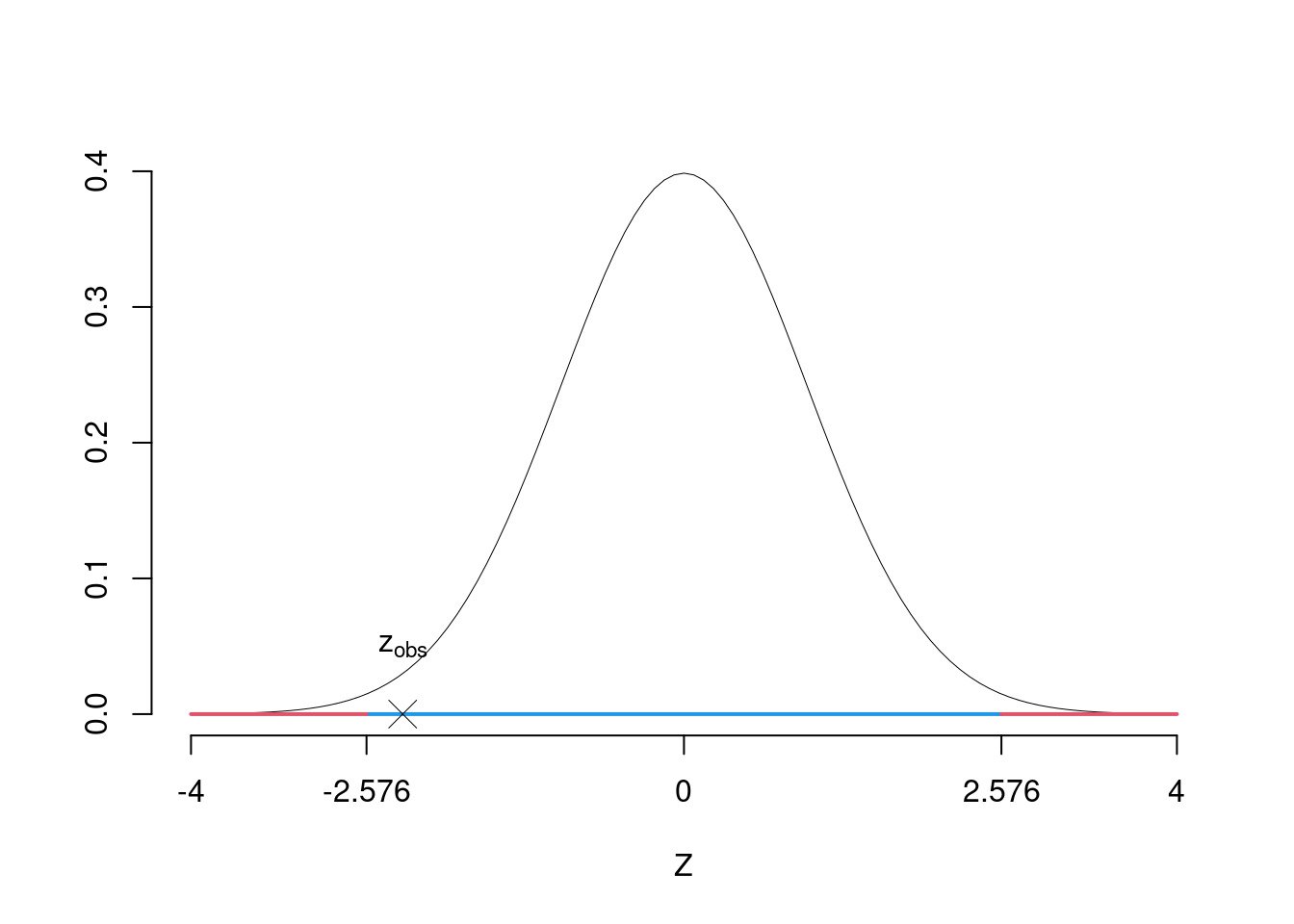
Il \(p_{\text{value}}\) è \[P(|Z|>|z_{\text{obs}}|)=2P(Z>|z_{\text{obs}}|)=2P(Z>| -2.28 |)= 0.02246\]
Esercizio 6
In uno studio sul potere d’acquisto delle famiglie è stato selezionato un campione di 150 nuclei familiari a cui è stato chiesto il reddito (\(X\)) e la percezione della perdita del potere d’acquisto espresso su una scala che va da zero a 1. Qui di seguito le statistiche bivariate
\[\begin{align*} \sum_{i=1}^n x_i &= 122.7102 &\sum_{i=1}^n x_i^2 &= 157.1624 &\sum_{i=1}^n x_i y_i &= 78.8937\\ \sum_{i=1}^n y_i &= 110.4192 & \sum_{i=1}^n y_i^2 &= 83.8077 & \end{align*}\]
6.a (Punti 14) Stimare la previsione per \(x=1.0\) nel modello di regressione dove \(Y\) viene spiegata da \(X\).
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{150} 122.7102= 0.8181\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{150} 110.4192= 0.7361\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{150} 157.1624 -0.8181^2=0.1389\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{150} 83.8077 -0.7361^2=0.0168\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{150} 78.8937-0.8181\cdot0.7361=-0.0762\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{-0.0762}{0.1389} = -0.2014\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 0.7361-(-0.2014)\times 0.8181=0.9009 \end{eqnarray*}\]
\[\hat y_{X= 1 }=\hat\beta_0+\hat\beta_1 x= 0.9009 + (-0.2014) \times 1 = 0.6995 \]
6.b (Punti 3) Il modello si adatta bene ai dati?
\[\begin{eqnarray*} r&=&\frac{\text{cov}(X,Y)}{\sigma_X\sigma_Y}=\frac{ -0.07624 }{ 0.6152 \times 0.1297 }= -0.9552 \\r^2&=& 0.9124 > 0.75 \end{eqnarray*}\] Il modello si adatta bene ai dati.
6.c (Punti 2) Cosa sono i punti di leva e cosa gli outliers?
6.d (Punti 2) Se \(W=10\times Y\), posto \[w_i=\beta_0'+\beta_1'x_ì +\epsilon_i'\] il modello in cui \(W\) viene spiegata da \(X\), quanto varranno \(\beta_0'\) e \(\beta_1'\)?
\[\begin{eqnarray*} \bar w &=& 10\times \bar y\\ &=& 7.3613\\ \sum x_iw_i&=&\sum x_i\cdot 10\cdot y_i\\ &=& 10\sum x_i y_i\\ &=& 788.9371\\ cov(x,w)&=&\sum x_iw_i-\bar w\cdot\bar x\\ &=&10\sum x_i y_i - 10 \cdot\bar y\cdot\bar x\\ &=&10 cov(x,y)\\ &=& -0.7624\\ \hat\beta'_1&=&\frac{10\cdot cov(x,y)}{\hat\sigma_X^2}\\ &=&-2.0143\\ \hat\beta_0'&=& \bar w -\hat\beta'_1\bar x\\ &=&10\bar y - 10 \hat \beta_1\bar x\\ &=&9.0091 \end{eqnarray*}\]
Prova di Statistica 2022/06/16-3
Esercizio 1
Su un campione di \(250\) famiglie della provincia di Ferrara è stato rilevata la spesa in generi alimentari (espresso in migliaia di euro). Qui di seguito i dati raccolti in classe e le frequenze assolute
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(n_j\) |
|---|---|---|
| 0 | 3 | 18 |
| 3 | 5 | 98 |
| 5 | 10 | 89 |
| 10 | 20 | 45 |
| 250 |
1.a (Punti 14) Individuare la classe modale.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|---|
| 0 | 3 | 7.2 | 18 | 0.072 | 3 | 2.40 | 0.072 |
| 3 | 5 | 39.2 | 98 | 0.392 | 2 | 19.60 | 0.464 |
| 5 | 10 | 35.6 | 89 | 0.356 | 5 | 7.12 | 0.820 |
| 10 | 20 | 18.0 | 45 | 0.180 | 10 | 1.80 | 1.000 |
| 100.0 | 250 | 1.000 | 20 |
1.b (Punti 3) Qual è la percentuale di famiglie con spesa superiore al 25-esimo percentile?
\[n\cdot 0.75=187.5\]
1.c (Punti 2) La spesa media è pari a \(\bar x=7.143\), che forma ci dobbiamo aspettare dell’istogramma di densità?
1.d (Punti 2) La varianza della spesa è pari a \(Var=19.055\). Se ogni famiglia aumentasse la sua spesa del 10%, quanto varrebbe standard deviation dei dati così trasformati?
\[\sigma_{new}=\sqrt{1.1^2\times \sigma^2}=4.5783\]
Esercizio 2
Siano \(X\sim \text{Binom}(5,0.4)\) e sia \(Y\sim \text{Binom}(2,0.4)\), \(X\) e \(Y\) indipendenti. Posto \(W=X+Y\)
2.a (Punti 14) Calcolare \(P(W< 2)\).
\[\begin{eqnarray*} W &\sim& \text{Binom}(2+5,0.4)\\ P(W<2) &=& P(W=0)+P(W=1)\\ &=& \binom{7}{0}0.4^00.6^7+\binom{7}{1}0.4^10.6^6\\ &=& 0.028+0.1306\\ &=&0.1586 \end{eqnarray*}\]
2.b (Punti 3) Posto \(V=2+5\cdot W\), ricavare valore atteso e varianza di \(V\).
\[\begin{eqnarray*} E(V) &=& 2+5E(X) \\ &=& 2+5\times 7 \times 0.4\\ &=& 16\\ V(V) &=& 5^2V(X) \\ &=& 25\times 7\times 0.4\times (1-.04)\\ &=& 42\\ \end{eqnarray*}\]
2.c (Punti 2) Se \(A\) e \(B\) sono due eventi diversi dal vuoto, è possibile che \(P(A)+P(B)>1\)?
Esercizio 3
3.a (Punti 14) Un’urna contiene 3 palline bianche, 2 nere e 5 blu. Si estrae 200 volte con reimmissione. Calcolare la probabilità che il numero di palline nere sia maggiore di 50.
\(E(X_i)=0.2\), \(V(X_i)=0.16\) e quindi
Teorema del Limite Centrale (somma di Bernoulli)
Siano \(X_1\),…,\(X_n\), \(n=200\) VC IID, tc \(X_i\sim\text{Ber}(\pi=0.2)\)\(,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\pi,n\pi(1-\pi)) \\ &\sim & N(200\cdot0.2,200\cdot0.2\cdot(1-0.2)) \\ &\sim & N(40,32) \end{eqnarray*}\]
\[\begin{eqnarray*} P(S_n > 50) &=& P\left( \frac {S_n - n\pi}{\sqrt{n\pi(1-\pi)}} > \frac {50 - 40}{\sqrt{32}} \right) \\ &=& P\left( Z > 1.77\right) \\ &=& 1-P(Z< 1.77 )\\ &=& 1-\Phi( 1.77 ) \\ &=& 0.0384 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(\hat \lambda\) lo stimatore di massima verosimiglianza di \(\lambda\) del modello Poisson. \[\begin{eqnarray*} \hat\lambda &=& \frac 1n\sum_{i=1}^nx_i\\ \end{eqnarray*}\] Dimostrare le consistenza di \(\hat\lambda\) in almeno tre passaggi.
4.b (Punti 2) Siano \(h\) uno stimatore per \(\theta\), cosa significa dire che \(h\) è asintoticamente corretto?
4.c (Punti 3) Definire la probabilità di significatività.
4.d (Punti 3) Se in un test statistico \(0.01 < p_\text{value} <0.05\) cosa possiamo concludere?
Esercizio 5
(Punti 14) In un’indagine sull’opinione sul reddito sono stati rilevati i redditi di 140 persone che vivono al nord e quelli di 170 che vivono al sud: il reddito medio di chi vive al nord è di 32.2 mila euro annui con una SD pari a 2.4 mila euro annui, mentre il reddito medio di chi vive al sud è di 27.5 con una SD pari a 1.7.
Sotto ipotesi di eterogeneità testare al 5 percento l’ipotesi che il reddito medio sia uguale al nord come al sud, contro l’alternativa che sia diverso.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0:\mu_\text{N} = \mu_\text{ S}\text{}\\ H_1:\mu_\text{N} \neq \mu_\text{ S}\text{} \end{cases}\] Siccome \(H_1\) è bilaterale, considereremo \(\alpha/2\), anziché \(\alpha\)
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(T\)
L’ipotesi è di eterogeneità e quindi calcoliamo: \[ S^2_\text{N}=\frac{n_\text{N}}{n_\text{N}-1}\hat\sigma^2_\text{N}=\frac{140}{140-1}2.4^2=5.8014 \qquad S^2_\text{S}=\frac{n_\text{S}}{n_\text{S}-1}\hat\sigma^2_\text{S}=\frac{170}{170-1}1.7^2=2.9071 \]
\[\begin{eqnarray*} \frac{\hat\mu_\text{N} - \hat\mu_\text{S}} {\sqrt{\frac {S^2_\text{N}}{n_\text{N}}+\frac {S^2_\text{S}}{n_\text{S}}}}&\sim&t_{n_\text{N}+n_\text{S}-2}\\ t_{\text{obs}} &=& \frac{ (32.2- 27.5)} {\sqrt{\frac{5.8014}{140}+\frac{2.9071}{170}}} = 19.4256\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE
Dalle tavole si ha \(t_{(140+170-2);\, 0.025} = 1.9677\). \[t_{\text{obs}} = 19.4256 > t_{308;\, 0.025} = 1.9677\]
CONCLUSIONE: i dati non sono coerenti con \(H_{0}\) al LdS del 5%
Graficamente
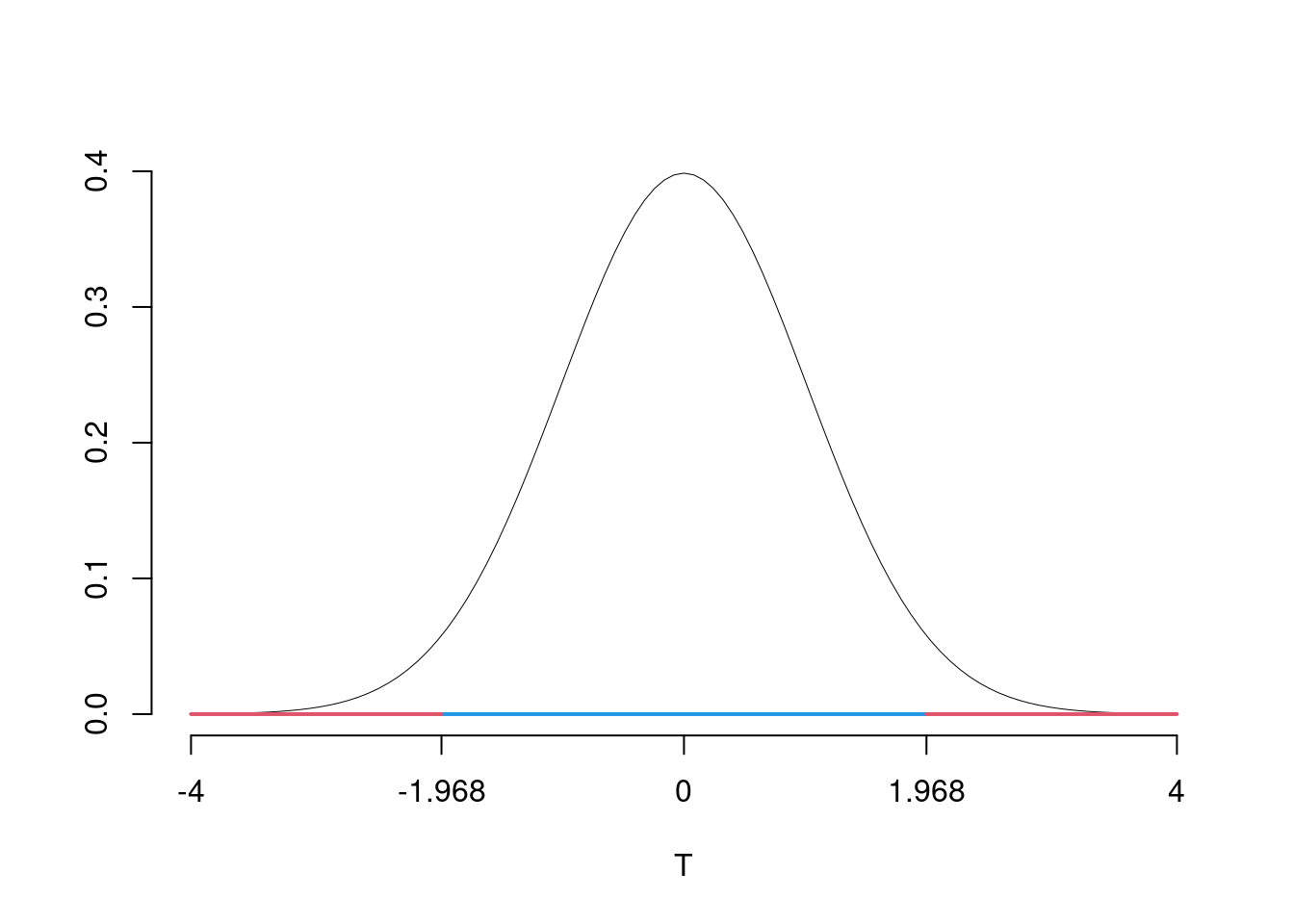
Il \(p_{\text{value}}\) è \[P(|T_{n1+n2-2}|>|t_{\text{obs}}|)=2P(T_{n1+n2-2}>|t_{\text{obs}}|)=2P(T_{n1+n2-2}>| 19.4256 |)= 1.958e-55\]
Esercizio 6
In uno studio sul potere d’acquisto delle famiglie è stato selezionato un campione di 150 nuclei familiari a cui è stato chiesto il reddito (\(X\)) e la percezione della perdita del potere d’acquisto espresso su una scala che va da zero a 1. Qui di seguito le statistiche bivariate
\[\begin{align*} \sum_{i=1}^n x_i &= 109.6214 &\sum_{i=1}^n x_i^2 &= 134.2159 &\sum_{i=1}^n x_i y_i &= 71.3992\\ \sum_{i=1}^n y_i &= 112.7445 & \sum_{i=1}^n y_i^2 &= 87.1782 & \end{align*}\]
6.a (Punti 14) Stimare la previsione per \(x=1.4\) nel modello di regressione dove \(Y\) viene spiegata da \(X\).
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{150} 109.6214= 0.7308\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{150} 112.7445= 0.7516\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{150} 134.2159 -0.7308^2=0.16\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{150} 87.1782 -0.7516^2=0.0162\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{150} 71.3992-0.7308\cdot0.7516=-0.0733\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{-0.0733}{0.16} = -0.2032\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 0.7516-(-0.2032)\times 0.7308=0.9002 \end{eqnarray*}\]
\[\hat y_{X= 1 }=\hat\beta_0+\hat\beta_1 x= 0.9002 + (-0.2032) \times 1 = 0.6969 \]
6.b (Punti 3) Calcolare e discutere \(R^2\).
\[\begin{eqnarray*} r&=&\frac{\text{cov}(X,Y)}{\sigma_X\sigma_Y}=\frac{ -0.0733 }{ 0.6006 \times 0.1274 }= -0.9578 \\r^2&=& 0.9173 > 0.75 \end{eqnarray*}\] Il modello si adatta bene ai dati.
6.c (Punti 2) Cos’è un punto influente?
6.d (Punti 2) Se \(W=10+ Y\), posto \[w_i=\beta_0'+\beta_1'x_ì +\epsilon_i'\] il modello in cui \(W\) viene spiegata da \(X\), quanto varranno \(\beta_0'\) e \(\beta_1'\)?
\[\begin{eqnarray*} \bar w &=& 10+ \bar y\\ &=& 10.7516\\ \sum x_iw_i&=&\sum x_i\cdot (10+y_i)\\ &=& 10\sum x_i +\sum x_i y_i\\ &=& 10n\bar x +\sum x_i y_i\\ cov(x,w)&=&\frac 1n\sum x_iw_i-\bar w\cdot\bar x\\ &=&10\bar x +\frac 1n\sum x_i y_i-\bar x(10+\bar y)\\ &=&10 \bar x - 10 \bar x +cov(x,y) \\ &=& -0.0733\\ \hat\beta'_1&=&\hat\beta_1\\ &=&-0.2032\\ \hat\beta_0'&=& \bar w -\hat\beta'_1\bar x\\ &=& 10+\bar y-\hat\beta_1\bar x\\ &=&10+\hat\beta_0\\ &=&10.9002 \end{eqnarray*}\]
Prova di Statistica 2022/07/01-1
Esercizio 1
Su un campione di \(220\) imprese energivore della provincia di Bologna è stato rilevata la spesa in investimenti green, espressa in migliaia di euro. Qui di seguito i dati raccolti in classi e le frequenze percentuali.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) |
|---|---|---|
| 0 | 7 | 16.742 |
| 7 | 15 | 39.819 |
| 15 | 17 | 36.652 |
| 17 | 20 | 6.787 |
| 100.000 |
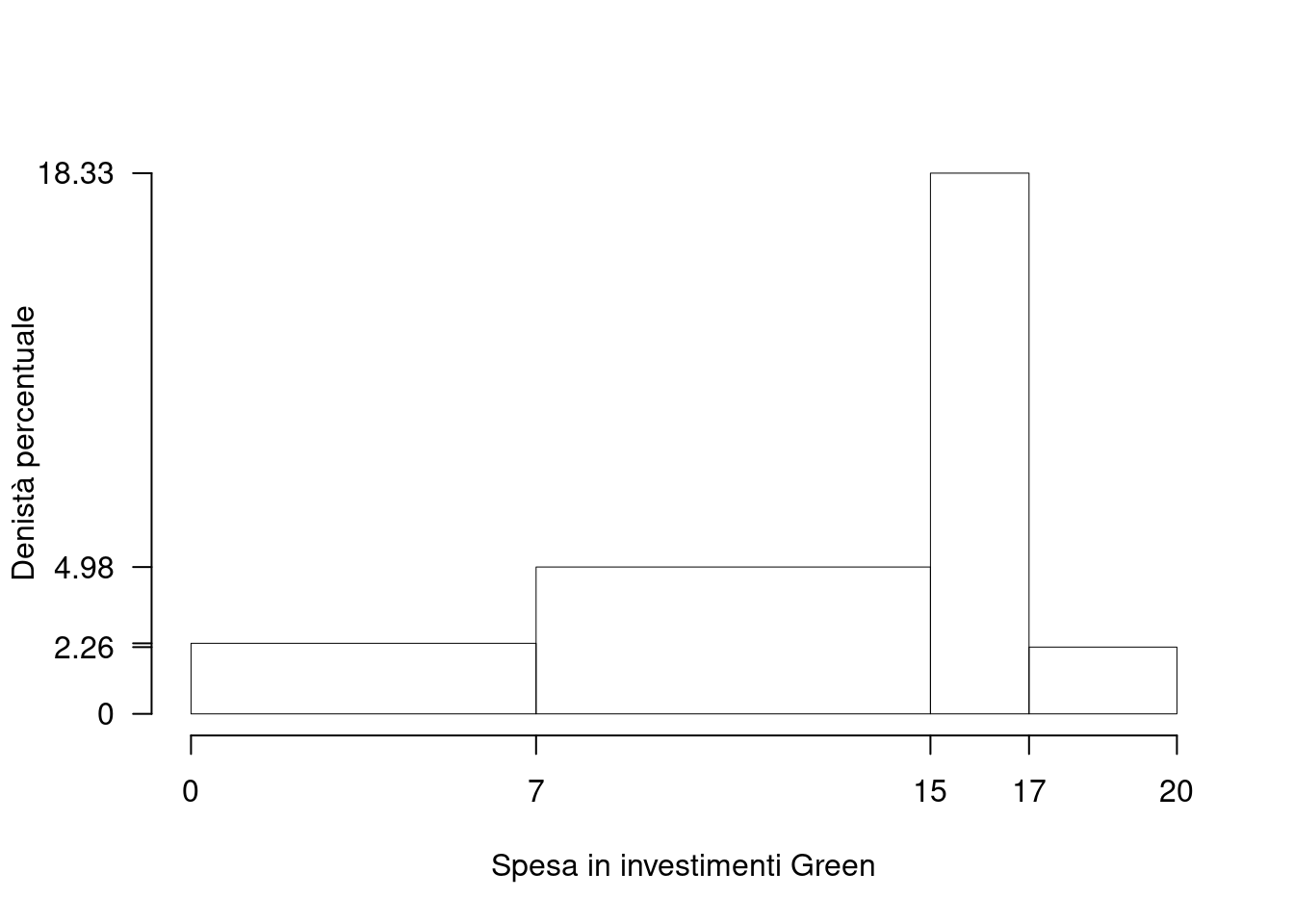
1.a (Punti 14) Individuare la classe modale.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|
| 0 | 7 | 37 | 0.1674 | 7 | 2.392 | 0.1674 |
| 7 | 15 | 88 | 0.3982 | 8 | 4.977 | 0.5656 |
| 15 | 17 | 81 | 0.3665 | 2 | 18.326 | 0.9321 |
| 17 | 20 | 15 | 0.0679 | 3 | 2.262 | 1.0000 |
| 221 | 1.0000 | 20 |
la classe modale è la classe \(`r `\) essendo la classe con densità \(h_{3}=18.3258\) maggiore.
1.b (Punti 3) Quante imprese hanno una spesa compresa tra 15 mila euro e il 75-esimo percentile?
\[\begin{eqnarray*} F(15)&=&0.5656\\ F(x_{0.75})&=&.75\\ \%(15<X<x_{0.75})&=&0.1844\\ n(15<X<x_{0.75})&=&40.5656 \end{eqnarray*}\]
1.c (Punti 2) La spesa media è pari a \(\bar x=12.0473\) mila euro, considerato la classe modale ricavata al punto 1.a, quale relazione ci dobbiamo attendere tra media e mediana?
1.d (Punti 2) La spesa media in investimenti green su 220 aziende modenesi è pari a \(\bar x=12.0473\) mila euro, mentre la spesa media in investimenti green della provincia di Reggio, su un campione di 150 aziende è pari a \(12.22\) mila euro. Calcolare la media globale delle \(220 + 150 = 370\) aziende delle due province.
\[\begin{eqnarray*} \bar x_T&=&\frac{220\times12.0473+150\times12.22}{220+150}\\ &=& 12.1173 \end{eqnarray*}\]
Esercizio 2
Siano \(X\sim N(10,1)\) e sia \(Y\sim N(10,1)\), \(X\) e \(Y\) indipendenti. Posto \(A=\{X>8\}\), \(B=\{X>11\}\), e \(C=\{9<Y\le 10\}\).
2.a (Punti 14) Quanto vale \(P\Big((A\cup B)\cup C\Big)\)?
\[\begin{eqnarray*} P(A\cup B)&=&P(A) \end{eqnarray*}\]
\[\begin{eqnarray*} P(X > 8) &=& P\left( \frac {X - \mu_X}{\sigma_X} > \frac {8 - 10}{\sqrt{1}} \right) \\ &=& P\left( Z > -2\right) \\ &=& 1-P(Z< -2 )\\ &=& 1-(1-\Phi( 2 )) \\ &=& 0.9772 \end{eqnarray*}\]
\[\begin{eqnarray*} P(9<X\leq 10) &=& P\left( \frac {9 - 10}{\sqrt{1}} < \frac {X - \mu}{\sigma} \leq \frac {10 - 10}{\sqrt{1}}\right) \\ &=& P\left( -1 < Z \leq 0\right) \\ &=& \Phi(0)-\Phi(-1)\\ &=& \Phi( 0 )-(1-\Phi( 1 )) \\ &=& 0.5 -(1- 0.8413 ) \\ &=& 0.3413 \end{eqnarray*}\]
\[\begin{eqnarray*} P(A\cup B\cup C)&=&P(A\cup C)\\ &=&P(A)+P(C)-P(A\cap C)\\ &=& 0.9772 +0.3413-0.9772\times 0.3413\\ &=& 0.985 \end{eqnarray*}\]
2.b (Punti 3) Sia \(X\sim N(10,1)\), posto \(A=\{X>8\}\). Si estrae ripetutamente da \(X\) e si finisce quando \(A\) si avvera 2 volte. Calcolare la probabilità di finire dopo 6 estrazioni.
\[\begin{eqnarray*} P(A)&=&0.9772\\ P(\text{vincere alla sesta})&=&5\times0.9772\times (0.0228)^4\times 0.9772\\ &=& 0 \end{eqnarray*}\]
2.c (Punti 2) Siano \(A\) e \(B\) due eventi diversi dal vuoto. È vero che se \(A\) e \(B\) sono non indipendenti, allora sono necessariamente incompatibili?
No, se sono incompatibili allora sono certamente non indipendenti, in quato \[ P(A\cap B)=P(\emptyset)=0\ne P(A)P(B) \] mentre se non sono indipendenti \[ P(A\cap B)\ne P(A)P(B) \]
2.d (Punti 2) Se \(F\) è la funzione di ripartizione della VA \(X\), quali sono il valore massimo e quello minimo che \(F\) può assumere?
Esercizio 3
(Punti 14) Ogni giorno il centralino di un servizio di assistenza riceve in media 26.34 telefonate con una deviazione standard pari a 1.3 telefonate.
Dopo un anno (\(n=365\)), qual è la probabilità che il numero totale di telefonate sia compresa tra 9550 e 9600?
Teorema del Limite Centrale (somma VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=365\) VC IID, tc \(E(X_i)=\mu=26.34\) e \(V(X_i)=\sigma^2=1.69,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\mu,n\sigma^2) \\ &\sim & N(365\cdot26.34,365\cdot1.69) \\ &\sim & N(9614,616.9) \end{eqnarray*}\]
\[\begin{eqnarray*} P(9550<S_n\leq 9600) &=& P\left( \frac {9550 - 9614.1}{\sqrt{616.85}} < \frac {S_n - n\mu}{\sqrt{n\sigma^2}} \leq \frac {9600 - 9614.1}{\sqrt{616.85}}\right) \\ &=& P\left( -2.58 < Z \leq -0.57\right) \\ &=& \Phi(-0.57)-\Phi(-2.58)\\ &=& (1-\Phi( 0.57 ))-(1-\Phi( 2.58 )) \\ &=& (1- 0.7157 )-(1- 0.9951 ) \\ &=& 0.2794 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(\hat \lambda\) lo stimatore di massima verosimiglianza di \(\lambda\) del modello di Poisson: \(\hat\lambda = \frac 1n\sum_{i=1}^nx_i\) Scrivere lo Standard Error di \(\hat \lambda\).
4.b (Punti 3) Se \(h\) è uno stimatore per \(\theta\) tale che \(E(h)\ne \theta\) e che \(\lim_ {n\to +\infty}E(h)=\theta\) di quale proprietà gode \(h\)?
4.c (Punti 3) Definire gli errori di primo e di secondo tipo di un test statistico e le relative probabilità.
4.d (Punti 3) In un confronto tra due campioni viene messo a test \[ \begin{cases} H_0:\sigma_A=\sigma_B\\ H_1:\sigma_A\ne \sigma_B \end{cases} \] Il \(p_\text{value}=0.265\). Alla luce di questo risultato, per testare la differenza tra le medie, cosa è preferibile, un test sotto ipotesi di omogeneità, oppure sotto ipotesi di eterogeneità?
Esercizio 5
Su un campione di \(n_M=34\) consumatori privati, scelti a caso tra i cittadini del comune di Mirandola, si è chiesto quanto spenderebbero mensilmente per poter usufruire di una connessione ultra veloce. Il campione ha restituito una media pari a 19.4 €/mese, con una deviazione standard pari a 2.2 €/mese,
(Punti 7) Costruire un Intervallo di Confidenza al 95% per la media di popolazione \(\mu\).
\[ S =\sqrt{\frac {n}{n-1}}\cdot\hat\sigma = \sqrt{\frac { 34 }{ 33 }}\cdot 2.2 = 2.2331 \] \[\begin{eqnarray*} Idc: & & \hat\mu \pm t_{n-1;\alpha/2} \times \frac{S}{\sqrt{n}} \\ & & 19.4 \pm 2.035 \times \frac{ 2.2331 }{\sqrt{ 34 }} \\ & & 19.4 \pm 2.035 \times 0.383 \\ & & [ 18.62 , 20.18 ] \end{eqnarray*}\]
(Punti 7) La stessa domanda è stata posta ad un secondo campione di \(n_S=38\) consumatori privati,scelti a caso tra i cittadini del comune di Sassuolo. Il campione ha restituito una media pari a 20.2 €/mese, con una deviazione standard pari a 2.9 €/mese. Sotto ipotesi di omogeneità testare al 5% l’ipotesi che i due comuni abbiano uguale media, contro l’alternativa che sia diversa.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0:\mu_\text{1} = \mu_\text{ 2}\text{}\\ H_1:\mu_\text{1} \neq \mu_\text{ 2}\text{} \end{cases}\] Siccome \(H_1\) è bilaterale, considereremo \(\alpha/2\), anziché \(\alpha\)
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(T\)
L’ipotesi è di omogeneità e quindi calcoliamo:
\[ S_p^2=\frac{n_\text{1}\hat\sigma^2_\text{1}+n_\text{2}\hat\sigma^2_\text{2}}{n_\text{1}+n_\text{2}-2} = \frac{34\cdot2.2^2+38\cdot2.8^2}{34+38-2}=6.6069 \]
\[\begin{eqnarray*} \frac{\hat\mu_\text{1} - \hat\mu_\text{2}} {\sqrt{\frac {S^2_p}{n_\text{1}}+\frac {S^2_p}{n_\text{2}}}}&\sim&t_{n_\text{1}+n_\text{2}-2}\\ t_{\text{obs}} &=& \frac{ (19.4- 20.2)} {\sqrt{\frac{6.6069}{34}+\frac{6.6069}{38}}} = -1.3184\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(t_{(34+38-2);\, 0.025} = -1.9944\). \[t_{\text{obs}} = -1.3184 > t_{70;\, 0.025} = -1.9944\]
CONCLUSIONE: i dati sono coerenti con \(H_{0}\) al LdS del 5%
Graficamente
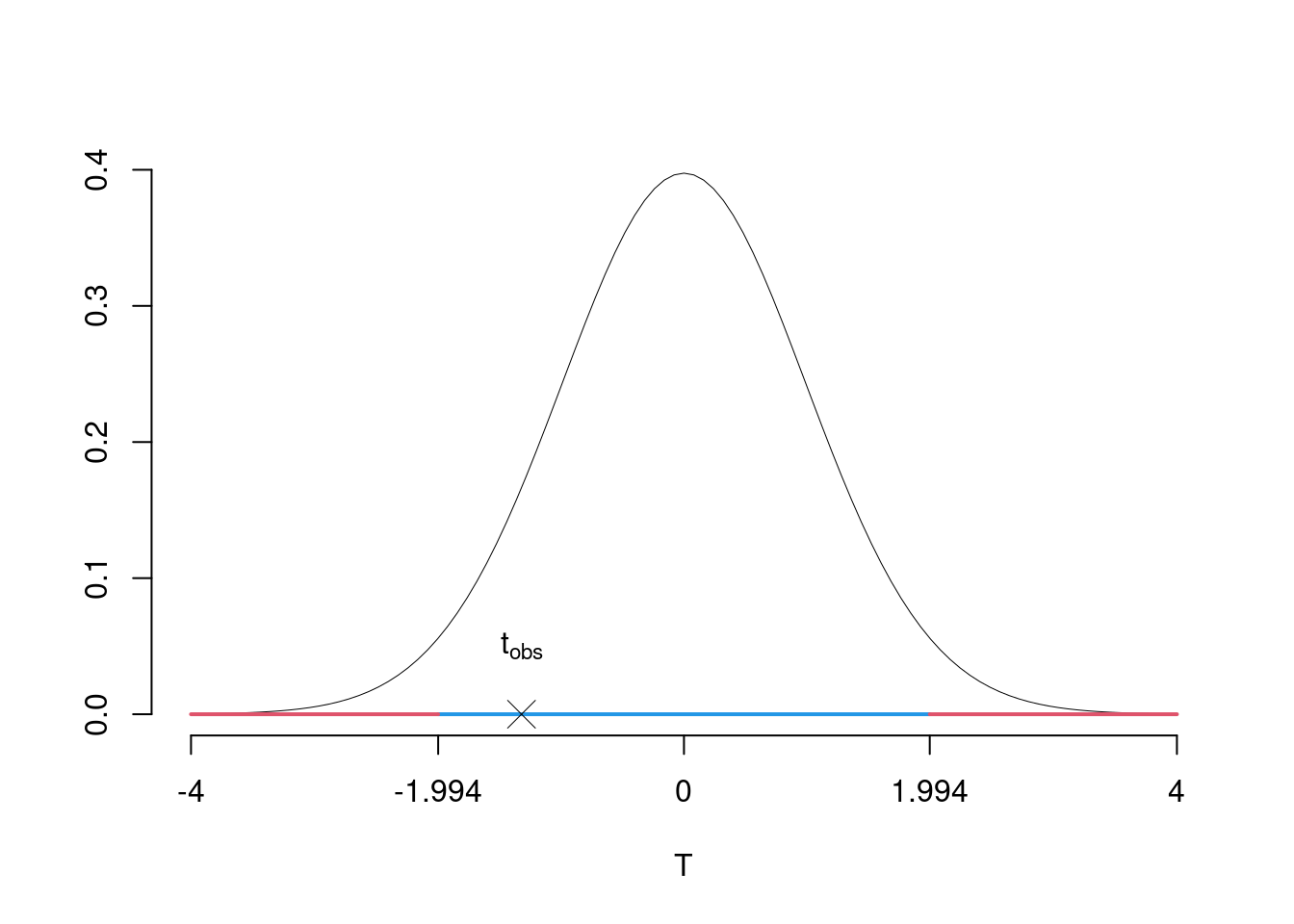
Il \(p_{\text{value}}\) è \[P(|T_{n1+n2-2}|>|t_{\text{obs}}|)=2P(T_{n1+n2-2}>|t_{\text{obs}}|)=2P(T_{n1+n2-2}>| -1.3184 |)= 0.1917\]
Esercizio 6
Sono stati analizzati 5 comuni della provincia di Modena e su ogni comune è stato rilevato il numero di abitanti \(X\), espresso in migliaia di persone, e il numero di esercizi commerciali \(Y\).
Qui di seguito i dati
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| \(x_i\) | 12.20 | 12.40 | 13.50 | 18.40 | 19.80 |
| \(y_i\) | 6.72 | 6.33 | 9.34 | 8.52 | 14.15 |
6.a (Punti 14) Calcolare il residuo del quarto dato nel modello di regressione dove \(Y\) viene spiegata da \(X\).
| \(i\) | \(x_i\) | \(y_i\) | \(x_i^2\) | \(y_i^2\) | \(x_i\cdot y_i\) |
|---|---|---|---|---|---|
| 1 | 12.20 | 6.720 | 148.8 | 45.18 | 82.00 |
| 2 | 12.40 | 6.330 | 153.8 | 40.05 | 78.48 |
| 3 | 13.50 | 9.340 | 182.2 | 87.26 | 126.11 |
| 4 | 18.40 | 8.520 | 338.6 | 72.51 | 156.68 |
| 5 | 19.80 | 14.150 | 392.0 | 200.18 | 280.14 |
| Totale | 76.30 | 45.060 | 1215.5 | 445.18 | 723.41 |
| Totale/n | 15.26 | 9.012 | 243.1 | 89.04 | 144.68 |
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{5} 76.3= 15.26\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{5} 45.0558= 9.0112\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{5} 1215.45 -15.26^2=1.69\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{5} 445.1903 -9.0112^2=7.8371\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{5} 723.415-15.26\cdot9.0112=7.1727\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{7.1727}{1.69} = 0.7017\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 9.0112-0.7017\times 15.26=-1.6963 \end{eqnarray*}\]
\[\begin{eqnarray*} \hat y_i &=&\hat\beta_0+\hat\beta_1 x_i=\\ &=& -1.696 + 0.7017 \times 18.4 = 11.21 \\ \hat \varepsilon_i &=& y_i-\hat y_i\\ &=& 8.515 - 11.21 = -2.699 \end{eqnarray*}\]
6.b (Punti 3) Scrivere la scomposizione della varianza del modello di regressione e calcolare la Total Sum of Squares (TSS), la Explained Sum of Squares (ESS) e la Residual Sum of Squares (RSS) dei dati analizzati sopra.
\[\begin{eqnarray*} r&=&\frac{\text{cov}(X,Y)}{\sigma_X\sigma_Y}=\frac{ 7.173 }{ 3.197 \times 2.799 }= 0.8014 \\r^2&=& 0.6422 < 0.75 \end{eqnarray*}\] Il modello non si adatta bene ai dati.
6.c (Punti 3) Il parametro di regressione \(\hat\beta_0\), in questo caso, è interpretabile?
6.d (Punti 2) Una previsione per \(x=40\) è attendibile? Perché?
6.e (Punti 2) Se \(W=5+ Y\), posto \(w_i=\beta_0'+\beta_1'x_ì +\epsilon_i'\) il modello in cui \(W\) viene spiegata da \(X\), quanto varranno \(\beta_0'\) e \(\beta_1'\)?
Prova di Statistica 2022/07/01-2
Esercizio 1
Su un campione di \(220\) imprese energivora della provincia di Bologna è stato rilevata la spesa in investimenti green, espressa in migliaia di euro. Qui di seguito i dati raccolti in classi e le frequenze percentuali.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) |
|---|---|---|
| 0 | 7 | 6.79 |
| 7 | 15 | 36.65 |
| 15 | 17 | 39.82 |
| 17 | 20 | 16.74 |
| 100.00 |
1.a (Punti 14) Disegnare l’istogramma delle densità percentuali.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|
| 0 | 7 | 15 | 0.068 | 7 | 0.97 | 0.068 |
| 7 | 15 | 81 | 0.367 | 8 | 4.58 | 0.434 |
| 15 | 17 | 88 | 0.398 | 2 | 19.91 | 0.833 |
| 17 | 20 | 37 | 0.167 | 3 | 5.58 | 1.000 |
| 221 | 1.000 | 20 |
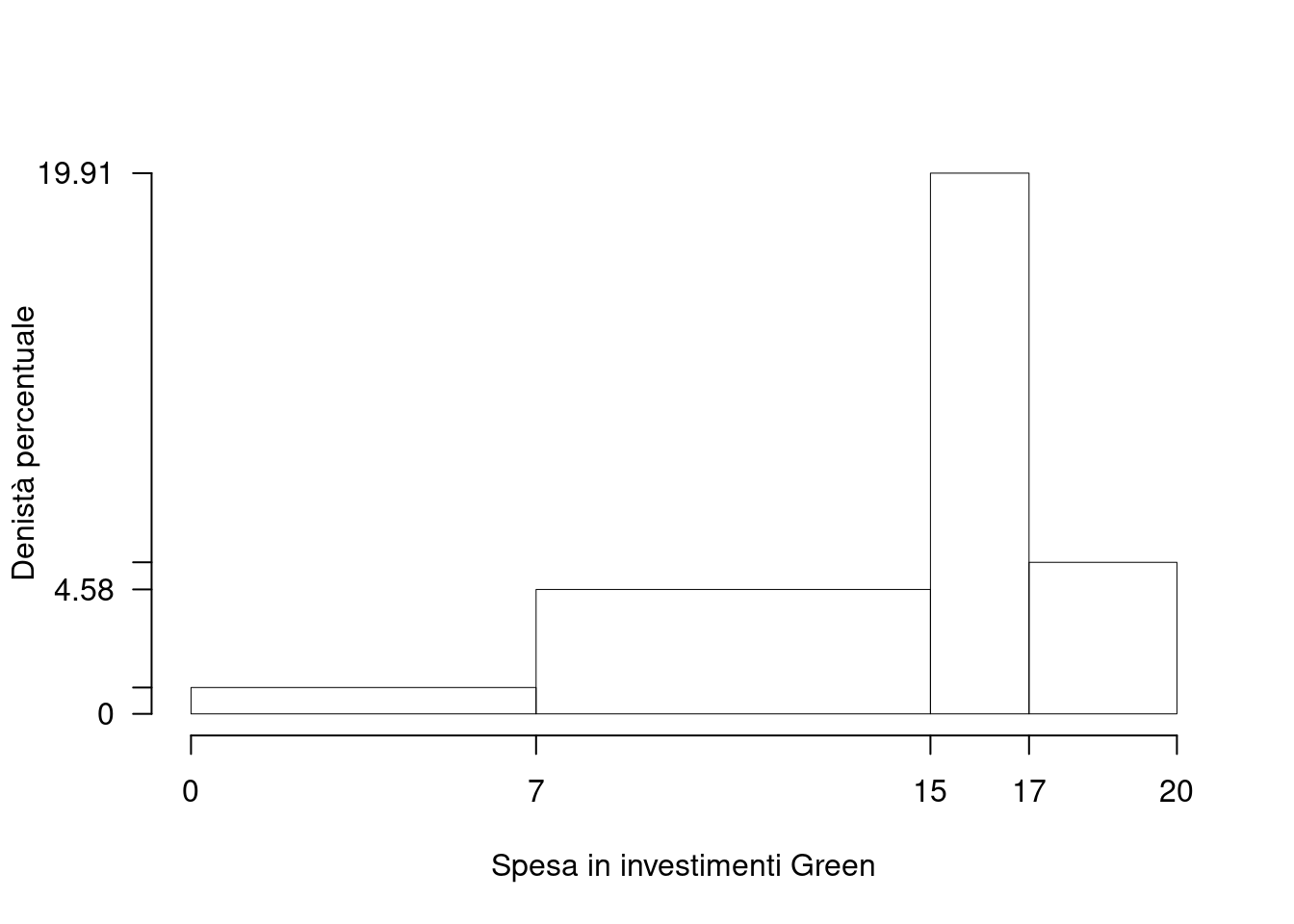
1.b (Punti 3) Quante aziende hanno una spesa compresa tra il 25-esimo percentile e 15 mila euro?
\[ 221(0.434-0.25)=40.664 \]
1.c (Punti 2) Che relazione dobbiamo attenderci tra media, mediana e moda?
1.d (Punti 2) La varianza della spesa è pari a \(Var=17.98\). Se ogni azienda aumentasse la sua spesa del 15%, quanto varrebbe varianza dei dati così trasformati?
Esercizio 2
Una rotatoria incrocia due strade, una che porta da nord a sud e una che porta da est ad ovest.
Il numero di automobili che impegna la rotatoria ogni minuto, in orario di punta,
| dalla direzione nord è descritto da una poisson di parametro 2.1 | \(X_N\sim\text{Pois}(2.1)\) |
| dalla direzione sud è descritto da una poisson di parametro 0.1 | \(X_S\sim\text{Pois}(0.1)\) |
| dalla direzione est è descritto da una poisson di parametro 1.4 | \(X_E\sim\text{Pois}(1.4)\) |
| dalla direzione ovest è descritto da una poisson di parametro 0.2 | \(X_O\sim\text{Pois}(0.2)\). |
Si assume l’indipendenza tra le variabili.
2.a (Punti 14) Si consideri l’evento \(E\)=“più di due veicoli impegnino la rotatoria”. Calcolare \(P(E)\).
\[ X\sim\text{Pois}(2.1+0.1+1.4+0.2) \]
\[P(X\ge 2) = 1-P(X<2)=1-0.022-0.085= 0.893\]
2.b (Punti 3) Si osserva la rotatoria per \(n=6\) minuti. Qual è la probabilità che il numero di volte in cui l’evento \(E\) è vero sia uguale a 3?
\[ P(\text{3 su 6})=\binom{6}{3}0.893^3(1-0.893)^3=0.018 \]
2.c (Punti 2) Se \(X\sim N(0,2)\) e \(X\sim N(1,1.2)\), è vero che \[ X-Y\sim N(-1,0.8) \qquad ? \]
2.d (Punti 2) Se \(X\) è una VC con supporto {0,1,2} e \(Y\) è una VC con supporto {2,3,4,5}. Qual è il supporto di \(X+Y\)?
il supporto di \(X+Y\) è \(\{2, 3, 4, 5, 6, 7\}\).
Esercizio 3
(Punti 14) Un’urna contiene 10 palline numerate da 1 a 10. Si vince se il numero estratto è divisibile per tre, altrimenti si perde. Si estrae 50 volte con reintroduzione.
Qual è la probabilità di vincere almeno 20 volte su 50 giocate?
\[ \pi=\frac 3{10} \]
Teorema del Limite Centrale (somma di Bernoulli)
Siano \(X_1\),…,\(X_n\), \(n=50\) VC IID, tc \(X_i\sim\text{Ber}(\pi=0.3)\)\(,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\pi,n\pi(1-\pi)) \\ &\sim & N(50\cdot0.3,50\cdot0.3\cdot(1-0.3)) \\ &\sim & N(15,10.5) \end{eqnarray*}\]
\[\begin{eqnarray*} P(S_n > 20) &=& P\left( \frac {S_n - n\pi}{\sqrt{n\pi(1-\pi)}} > \frac {20 - 15}{\sqrt{10.5}} \right) \\ &=& P\left( Z > 1.54\right) \\ &=& 1-P(Z< 1.54 )\\ &=& 1-\Phi( 1.54 ) \\ &=& 0.0618 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Siano \(h_1\) e \(h_2\) due stimatori per \(\theta\), tali che
\[ MSE(h_1) = \frac{\theta}{n^2}, \qquad MSE(h_2) = \frac{\theta}{n} \]
Quale dei due stimatori è più efficiente?
4.b (Punti 3) Siano \(T_1\) e \(T_2\) due test statistici per la stessa \(H_0\) e con la stessa significatività \(\alpha\). Cosa significa dire che \(T_1\) e più potente di \(T_2\)?
4.c (Punti 3) Definire la probabilità di significatività osservata.
4.d (Punti 3) Se in un test statistico che utilizza la statistica test t con 10 gradi di libertà \(t_\text{obs}=1.4\), il \(p_\text{value}\) sarà maggiore o minore di 0.05? Perché?
Esercizio 5
Su un campione di \(n=75\) abitanti del quartiere Q è stato chiesto se siano favorevoli o meno all’introduzione di corsie preferenziali per i mezzi pubblici. Lo studio ha riportato che 45 persone su 75 (il 60% del campione) è favorevole.
5.a (Punti 4) Costruire un intervallo di confidenza la 95% per \(\pi\) la quota di persone del quartiere Q favorevole alle corsie preferenziali
\[ \hat\pi = \frac{S_n}n = \frac{ 0.6 }{ 75 }= 0.008 \]
\[\begin{eqnarray*} Idc: & & \hat\pi \pm z_{\alpha/2} \times \sqrt{\frac{\hat\pi(1-\hat\pi)}{n}} \\ & & 0.008 \pm 1.96 \times \sqrt{\frac{ 0.008 (1- 0.008 )}{ 75 }} \\ & & 0.008 \pm 1.96 \times 0.0103 \\ & & [ -0.0122 , 0.0282 ] \end{eqnarray*}\]
5.b (Punti 10) Un’indagine molto più ampia condotta su tutta la città ha mostrato che la percentuale di favorevoli alle corsie preferenziali è del 55%. Testare al 5% l’ipotesi che nel quartiere Q la quota di favorevoli sia uguale a quella cittadina contro l’alternativa che sia maggiore.
La stima \[\hat\pi=\frac {45} {75}=0.6 \]
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\pi=\pi_0=0.55\\ H_1:\pi> \pi_0=0.55 \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)
Test Binomiale per \(n\) grande: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\pi - \pi_{0}} {\sqrt {\pi_0(1-\pi_0)/\,n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ (0.6- 0.55)} {\sqrt{0.55(1-0.55)/75}} = 0.87\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(z_{0.05} = 1.645\). \[z_{\text{obs}} = 0.87 < z_{0.05} = 1.645\] CONCLUSIONE: i dati sono coerenti con \(H_{0}\) al LdS del 5%
Graficamente
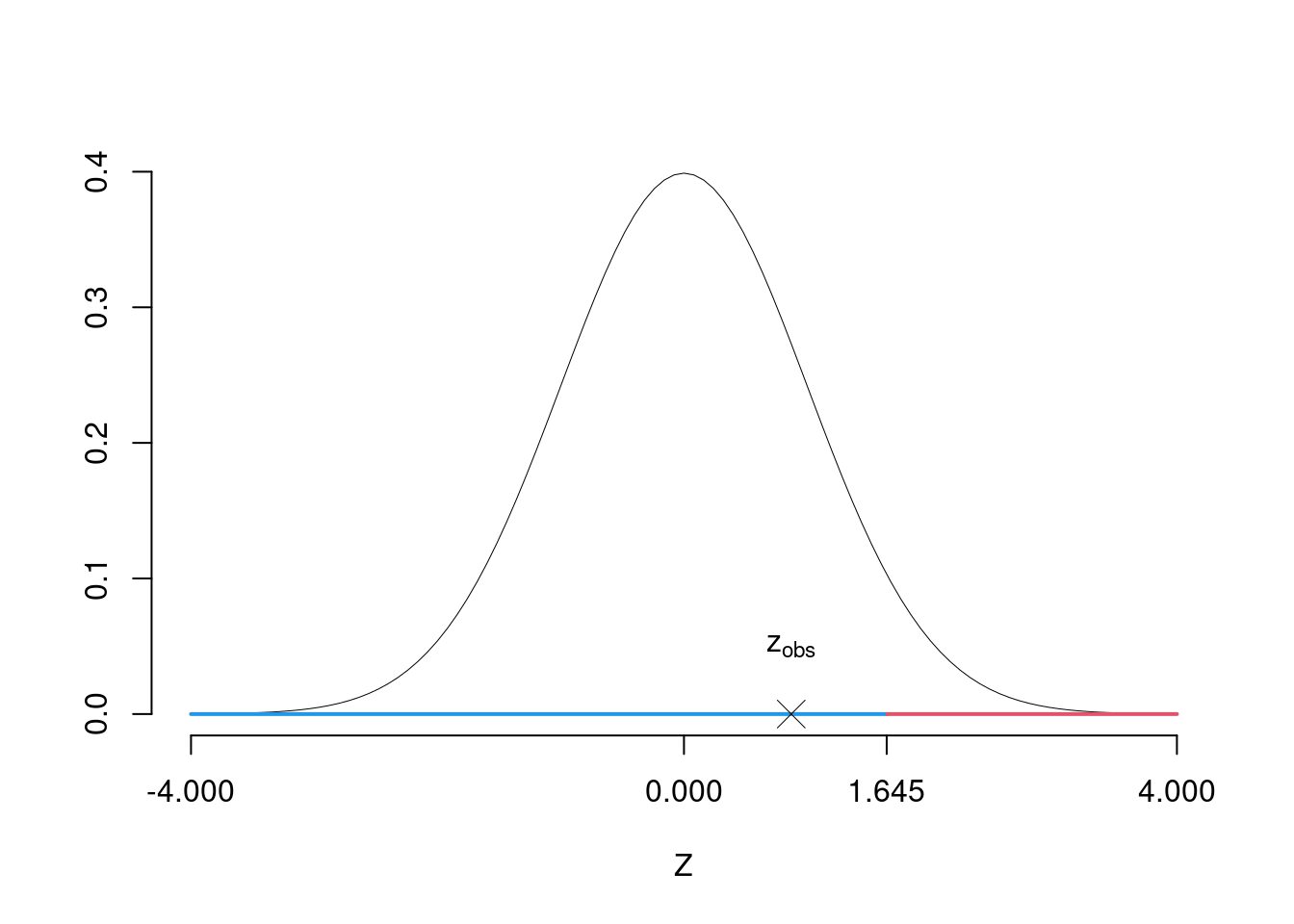
Il \(p_{\text{value}}\) è \[P(Z>z_{\text{obs}})=P(Z> 0.87 )= 0.192\]
Esercizio 6
Sono stati analizzati 50 comuni della provincia di Modena e su ogni comune è stato rilevato il numero di abitanti \(X\), espresso in migliaia di persone, e il numero di esercizi commerciali \(Y\).
Qui di seguito le statistiche bivariate
\[\begin{align*} \sum_{i=1}^n x_i &= 741.5 &\sum_{i=1}^n x_i^2 &= 11366.33 &\sum_{i=1}^n x_i y_i &= 7568.704\\ \sum_{i=1}^n y_i &= 483.933 & \sum_{i=1}^n y_i^2 &= 5757.604 & \end{align*}\]
6.a (Punti 14) Stimare la previsione per \(x=16\) nel modello di regressione dove \(Y\) viene spiegata da \(X\).
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{50} 741.5= 14.83\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{50} 483.9327= 9.679\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{50} 11366.33 -14.83^2=0.21\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{50} 5757.604 -9.6787^2=21.476\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{50} 7568.704-14.83\cdot9.6787=7.84\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{7.84}{0.21} = 1.06\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 9.679-1.0597\times 14.83=-6.037 \end{eqnarray*}\]
\[\hat y_{X= 16 }=\hat\beta_0+\hat\beta_1 x= -6.04 + 1.0597 \times 16 = 10.9 \]
6.b (Punti 3) Il modello si adatta bene ai dati?
\[r^2=0.387\]
6.c (Punti 2) Cosa sono i punti influenti?
6.d (Punti 2) Se \(W=2\times Y\) e \(V=X+3\), posto \(w_i=\beta_0'+\beta_1'v_ì +\epsilon_i'\) il modello in cui \(W\) viene spiegata da \(V\), quanto varranno \(\beta_0'\) e \(\beta_1'\)?
\[\begin{eqnarray*} \hat\beta_1' &=& r_{VW}\frac{\sigma_W}{\sigma_V} \\ &=& r_{XY}\frac{2\sigma_Y}{\sigma_X} \\ &=& 2\hat\beta_1\\ &=& 23.314\\ \hat\beta_0' &=& \bar w - \hat\beta_1'\bar v\\ &=& 2\bar y-2\hat\beta_1(\bar x + 3)\\ &=& -18.433 \end{eqnarray*}\]
Prova di Statistica 2022/07/01-3
Esercizio 1
Su un campione di \(220\) imprese energivora della provincia di Bologna è stato rilevata la spesa in investimenti green, espressa in migliaia di euro. Qui di seguito i dati raccolti in classi e le frequenze percentuali.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) |
|---|---|---|
| 0 | 3 | 16.74 |
| 3 | 5 | 39.82 |
| 5 | 13 | 36.65 |
| 13 | 20 | 6.79 |
| 100.00 |
1.a (Punti 14) Disegnare l’istogramma delle densità percentuali.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|
| 0 | 3 | 37 | 0.167 | 3 | 5.58 | 0.167 |
| 3 | 5 | 88 | 0.398 | 2 | 19.91 | 0.566 |
| 5 | 13 | 81 | 0.367 | 8 | 4.58 | 0.932 |
| 13 | 20 | 15 | 0.068 | 7 | 0.97 | 1.000 |
| 221 | 1.000 | 20 |
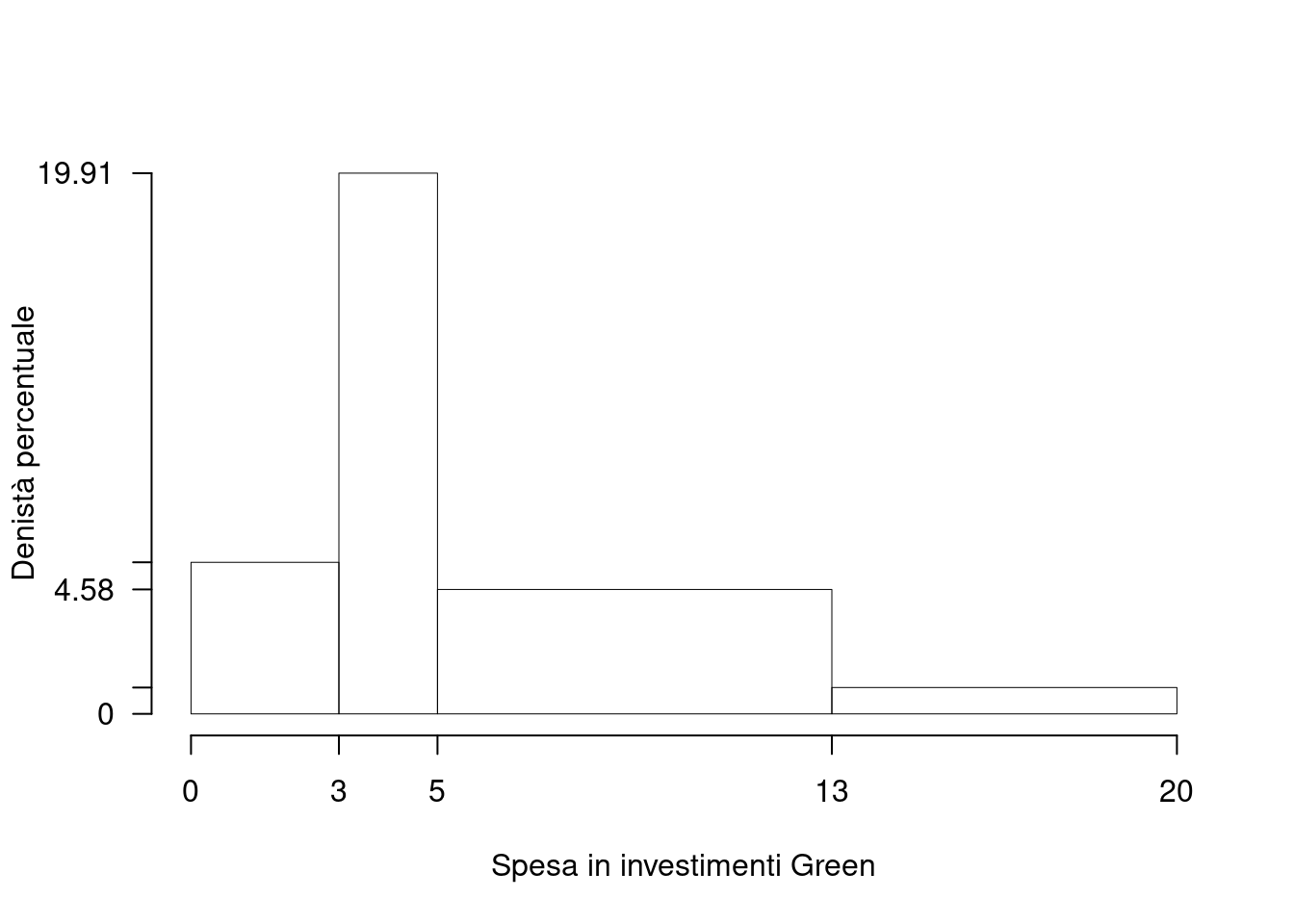
1.b (Punti 3) Qual è la percentuale di aziende che hanno una spesa compresa tra il 25-esimo percentile e 15 mila euro?
\[\begin{eqnarray*} \%(X<15) &=& F_3+(15-13)\times h_4\\ &=& 0.932\times 100+2\times 0.97\\ &=& 95.152\\ \%(X<x_{0.25}) &=& 25\%\\ \%(x_{0.25}<X<15)&=& 95.152-25\\ &=& 70.152 \end{eqnarray*}\]
1.c (Punti 2) Che relazione dobbiamo attenderci tra media, mediana e moda?
1.d (Punti 2) La varianza della spesa è pari a \(Var=17.282\). Se ogni azienda aumentasse la sua spesa di 10 mila euro, quanto varrebbe la media e la varianza dei dati così trasformati?
Esercizio 2
Una moneta perfetta viene lanciata 5 volte, se esce almeno 3 volte testa si estrae da un’urna che contiene un biglietto vincente ed uno perdente, altrimenti si estrae da un’urna che contine due biglietti vincenti e tre perdenti.
2.a (Punti 14) Qual è la probabilità di vincere?
\[\begin{eqnarray*} P(X=3) &=& 0.132\\ P(X=4) &=& 0.028\\ P(X=5) &=& 0.002\\ P(X\ge 3) &=& 0.5\\ P(\text{Vincere})&=& 0.5\frac12+(1-0.5)\frac23\\ &=& 0.583 \end{eqnarray*}\]
2.b (Punti 3) Si ripete il gioco di sopra finché non si vince due volte. Qual è la probabilità di finire alla quarta giocata?
\[ 3\times 0.583\times (1-0.583)^3\times 0.583 = 0.074 \]
2.c (Punti 2) Se \(X\sim \text{Pois}(2)\) e \(Y\sim\text{Pois}(1)\), è vero che \[ X-Y\sim\text{Pois}(1)\qquad ? \]
2.d (Punti 2) Se \(X\) è una VC con supporto {0,1,2} e \(X\) è una VC con supporto {-2,-1,0}. Qual è il supporto di \(X\times Y\)?
\[ \{-4,-2,-1,0\} \]
Esercizio 3
(Punti 14) Il supermercato S vende, in media ogni giorno, 102.3 kg di pasta, con una deviazione standard di 10.2. Dopo 60 giorni di apertura, qual è la probabilità che il totale di pasta venduta sia maggiore di 6700 kg?
Teorema del Limite Centrale (somma VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=60\) VC IID, tc \(E(X_i)=\mu=102\) e \(V(X_i)=\sigma^2=104,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\mu,n\sigma^2) \\ &\sim & N(60\cdot102,60\cdot104) \\ &\sim & N(6138,6242) \end{eqnarray*}\]
\[\begin{eqnarray*} P(S_n > 6700) &=& P\left( \frac {S_n - n\mu}{\sqrt{n\sigma^2}} > \frac {6700 - 6138}{\sqrt{6242.4}} \right) \\ &=& P\left( Z > 7.11\right) \\ &=& 1-P(Z< 7.11 )\\ &=& 1-\Phi( 7.11 ) \\ &=& 0 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Siano \(h_1\) e \(h_2\) due stimatori per \(\theta\), tali che
\[ MSE(h_1) = \frac{\theta}{n^2}, \qquad MSE(h_2) = \frac{\theta}{n^3} \]
Quale dei due stimatori è più efficiente?
4.b (Punti 3) Se uno stimatore \(h\) per \(\theta\) è tale che \(\lim_{n\to\infty}V(h)=0\), di quali proprietà gode \(h\)?
4.c (Punti 3) Un intervallo di confidenza per \(\theta\) al 95% è più ampio o meno ampio di uno al 99%? Perché?
4.d (Punti 3) Se in un test statistico che utilizza la statistica test t con 10 gradi di libertà \(t_\text{obs}=14\), il \(p_\text{value}\) sarà maggiore o minore di 0.05? Perché?
Esercizio 5
Su un campione di \(n=15\) abitanti del quartiere Q è stato chiesto di fornire un punteggio da 0 a 100 per esprimere quanto si sarebbe soddisfatti dall’introduzione di corsie preferenziali per i mezzi pubblici. Lo studio ha riportato una media pari a \(76.3\) e una deviazione standard pari a \(3.5\)
5.a (Punti 4) Costruire un intervallo di confidenza la 99% per \(\mu\) il punteggio medio che le persone del quartiere Q esprimono riguardo alle corsie preferenziali.
\[ S =\sqrt{\frac {n}{n-1}}\cdot\hat\sigma = \sqrt{\frac { 15 }{ 14 }}\cdot 3.5 = 3.6228 \] \[\begin{eqnarray*} Idc: & & \hat\mu \pm t_{n-1;\alpha/2} \times \frac{S}{\sqrt{n}} \\ & & 76.3 \pm 2.98 \times \frac{ 3.6228 }{\sqrt{ 15 }} \\ & & 76.3 \pm 2.98 \times 0.935 \\ & & [ 73.5 , 79.1 ] \end{eqnarray*}\]
5.b (Punti 10) Un’indagine molto più ampia condotta su tutta la città ha mostrato che il punteggio medio è pari a 66.3 con un deviazione standard pari a 3.3 .
Testare al 5% l’ipotesi che nel quartiere Q il punteggio medio sia uguale a quello cittadino contro l’alternativa che sia maggiore.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\mu=\mu_0=66.3\text{}\\ H_1:\mu> \mu_0=66.3\text{} \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\) \(\sigma^{2}\) di \(\cal{P}\) è nota: \(\Rightarrow\) z-Test. \[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {\sigma/\sqrt{n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ (76.3- 66.3)} {3.3/\sqrt{15}} = 11.736\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(z_{0.05} = 1.645\). \[z_{\text{obs}} = 11.736 > z_{0.05} = 1.645\]
CONCLUSIONE: i dati non sono coerenti con \(H_{0}\) al LdS del 5%
Graficamente
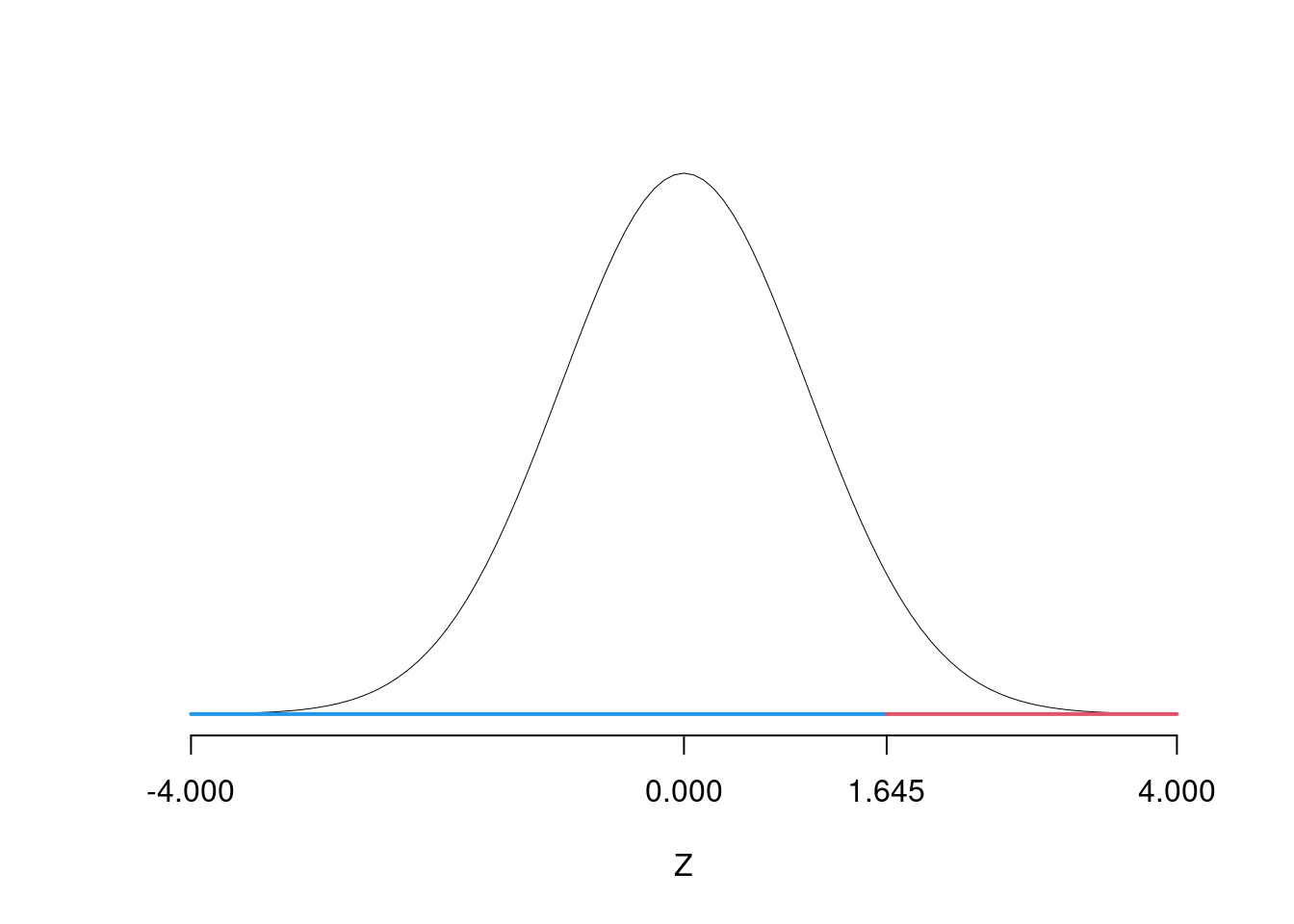
Il \(p_{\text{value}}\) è \[P(Z>z_{\text{obs}})=P(Z> 11.74 )= 0\]
Esercizio 6
Sono stati analizzati 50 comuni della provincia di Modena e su ogni comune è stato rilevato il numero di abitanti \(X\), espresso in migliaia di persone, e il numero di esercizi commerciali \(Y\).
Qui di seguito le statistiche bivariate
\[\begin{align*} \sum_{i=1}^n x_i &= 724 &\sum_{i=1}^n x_i^2 &= 10924.84 &\sum_{i=1}^n x_i y_i &= 7070.543\\ \sum_{i=1}^n y_i &= 455.063 & \sum_{i=1}^n y_i^2 &= 4962.848 & \end{align*}\]
6.a (Punti 14) Questi sono alcuni dei dati osservati
| \(x_i\) | 12.4 | 13.50 | 16.4 | 14.10 |
| \(y_i\) | 12.0 | 4.87 | 10.2 | 8.99 |
Calcolare il residuo per \(x=16.4\) nel modello di regressione dove \(Y\) è spiegato da \(X\).
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{50} 724= 14.48\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{50} 455.0632= 9.101\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{50} 10924.84 -14.48^2=104.04\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{50} 4962.848 -9.1013^2=16.424\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{50} 7070.543-14.48\cdot9.1013=9.625\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{9.625}{104.04} = 1.09\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 9.101-1.0904\times 14.48=-6.688 \end{eqnarray*}\]
\[\begin{eqnarray*} \hat y_i &=&\hat\beta_0+\hat\beta_1 x_i=\\ &=& -6.69 + 1.0904 \times 16.4 = 11.2 \\ \hat \varepsilon_i &=& y_i-\hat y_i\\ &=& 10.3 - 11.2 = -0.941 \end{eqnarray*}\]
6.b (Punti 3) Ricavare numericamente la scomposizione della varianza del modello di regressione sopra stimato.
\[\begin{eqnarray*} TSS &=& n\hat\sigma^2_Y\\ &=& 50 \times 16.4 \\ &=& 821 \\ ESS &=& R^2\cdot TSS\\ &=& 0.639 \cdot 821 \\ &=& 525 \\ RSS &=& (1-R^2)\cdot TSS\\ &=& (1- 0.639 )\cdot 821 \\ &=& 296 \\ TSS &=& RSS+TSS \\ 821 &=& 525 + 296 \end{eqnarray*}\]
6.c (Punti 2) Che differenza c’è tra interpolazione e estrapolazione?
6.d (Punti 2) Cosa significa che \(r\) è un numero puro?
Prova di Statistica 2022/07/27-1
Esercizio 1
Su un campione di \(220\) imprese della provincia di Milano è stato rilevato il bilancio, espresso in migliaia di euro, del 2020. Qui di seguito i dati raccolti in classi e le frequenze percentuali.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(f_{j\%}\) |
|---|---|---|
| 0 | 3 | 2.9 |
| 3 | 5 | 42.5 |
| 5 | 13 | 36.2 |
| 13 | 20 | 18.4 |
| 100.0 |
1.a (Punti 14) Individuare la classe modale.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|
| 0 | 3 | 6 | 0.029 | 3 | 0.966 | 0.029 |
| 3 | 5 | 88 | 0.425 | 2 | 21.256 | 0.454 |
| 5 | 13 | 75 | 0.362 | 8 | 4.529 | 0.816 |
| 13 | 20 | 38 | 0.184 | 7 | 2.622 | 1.000 |
| 207 | 1.000 | 20 |
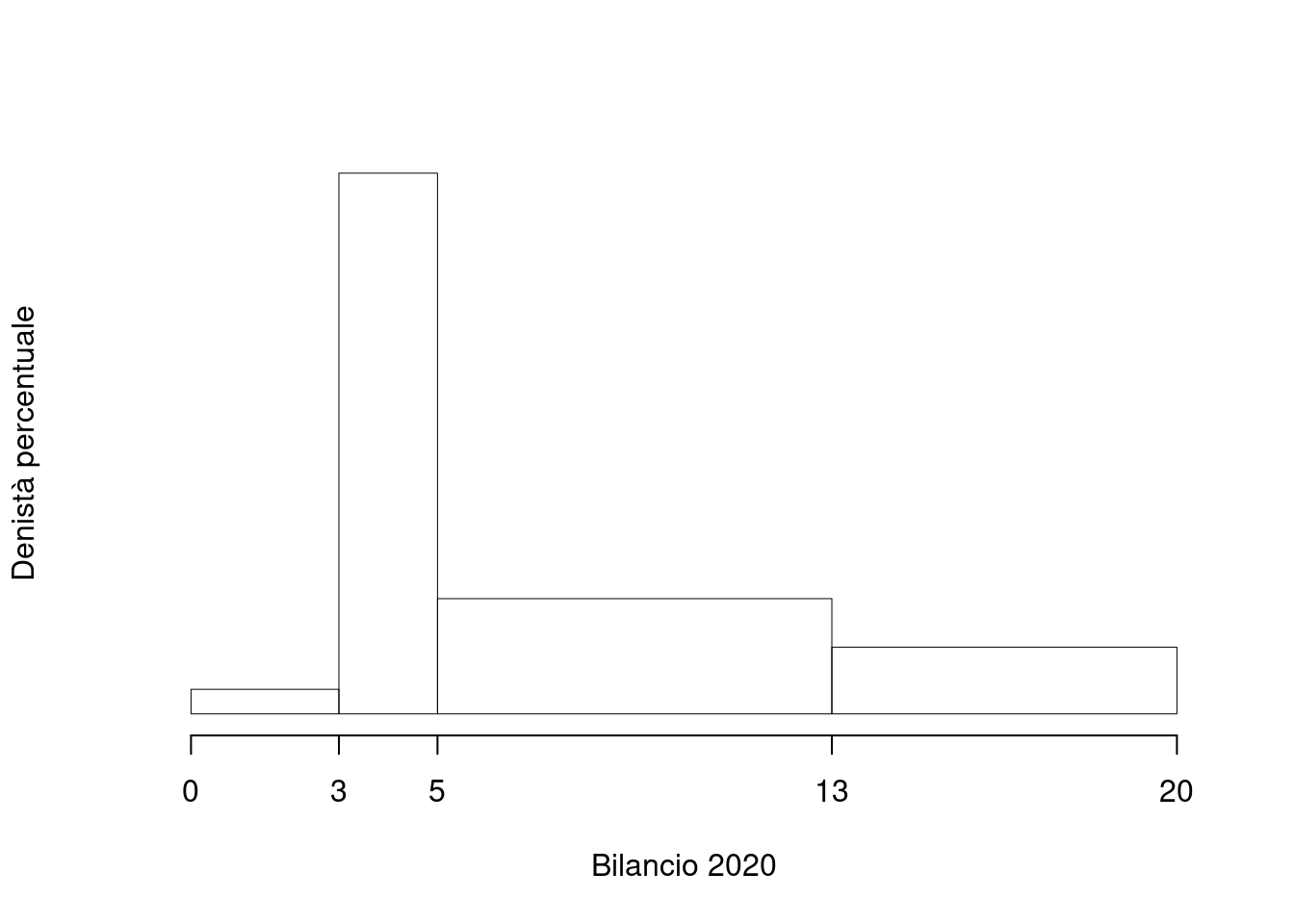
1.b (Punti 3) Quante imprese hanno un bilancio compreso tra \(-4\) mila euro e zero.
\[\#(-1<X<0)=\frac{(0-(-4))21.256}{100}\times 220=0\]
1.c (Punti 2) La media è risultata essere \(\bar x=7.958\); che relazione mi devo aspettare tra mediana e moda?
\[\bar x<x_{0.5}<x_{Mo}\]
1.d (Punti 2) Siano \(x_1,...,x_n\), \(n\) numeri, \(n\) dispari. Si consideri la funzione: \[g(x)=|x_1-x|+...+|x_n-x|.\] Per quale valore di \(x\), \(g(x)\) è minima?
La funzione \(g\) è minimizzata nel valore della mediana. \[x_{0.5}=x_{((n+1)/2)}\]
Esercizio 2
Siano \(X\sim N(5,1/2)\) e sia \(Y\sim N(5,1/2)\), \(X\) e \(Y\) indipendenti. Posto \(A=\{X>6\}\), \(B=\{Y<4\}\).
2.a (Punti 14) Calcolare \(P(A\cup B)\).
\[\begin{eqnarray*} P(X > 6) &=& P\left( \frac {X - \mu}{\sigma} > \frac {6 - 5}{\sqrt{0.5}} \right) \\ &=& P\left( Z > 1.41\right) \\ &=& 1-P(Z< 1.41 )\\ &=& 1-\Phi( 1.41 ) \\ &=& 0.0793 \end{eqnarray*}\]
\[\begin{eqnarray*} P(Y < 4) &=& P\left( \frac {Y - \mu_Y}{\sigma_Y} < \frac {4 - 5}{\sqrt{0.5}} \right) \\ &=& P\left( Z < -1.41\right) \\ &=& 1-\Phi( 1.41 ) \\ &=& 0.0793 \end{eqnarray*}\]
e quindi
\[\begin{eqnarray*} P(A\cup B) &=& P(A)+P(B)-P(A\cap B)\\ &=& 0.079+0.079-0.079\times0.079\\ &=& 0.151 \end{eqnarray*}\]
2.b (Punti 3) Posto \(Z=X-Y\), Calcolare la probabilità che \(P(Z>1|Z\le 2)\).
\[\begin{eqnarray*} Z &=& X-Y\\ &\sim& N(5-5,1/2+1/2)\\ &\sim& N(0,1)\\ P(Z>1|Z\le 2) &=&\frac{P(\{Z>1\}\cap\{Z\le 2\})}{P(Z\le 2)} \\ &=& \frac{P(1<Z\le 2)}{P(Z\le 2)} \\ &=&\frac{\Phi(2)-\Phi(1)}{\Phi(2)}\\ &=&\frac{0.977-0.841}{0.977}\\ &=&0.139 \end{eqnarray*}\]
2.c (Punti 2) Siano \(A\) e \(B\) due eventi diversi dal vuoto. Sono noti \(P(A|B)=0.3\), \(P(A|\bar B)=0.15\). \(A\) e \(B\) sono indipendenti? Perché?
No, perché se lo fossero \[ P(A|B)=P(A|\bar B)=P(A) \]
2.d (Punti 2) Sia \(X\sim\text{Pois}(\lambda=1)\), disegnare la funzione di ripartizione \(F(x)\) di \(X\), per \(x\) compreso tra \(-1\) e \(2.5\).

Esercizio 3
(Punti 14) Un’urna contiene tre palline, una Rossa, una Blue e una Nera. Si vince se esce Rossa. Si ripete il gioco per \(144\) volte. Qual è la probabilità che la proporzione di vincite sia maggiore di 0.35?
Teorema del Limite Centrale (proporzione)
Siano \(X_1\),…,\(X_n\), \(n=144\) VC IID, tc \(X_i\sim\text{Ber}(\pi=0.333)\)\(,\forall i\), posto: \[ \hat\pi=\frac{S_n}n = \frac{X_1 + ... + X_n}n \] allora:\[\begin{eqnarray*} \hat\pi & \mathop{\sim}\limits_{a}& N(\pi,\pi(1-\pi)/n) \\ &\sim & N\left(0.333,\frac{0.333\cdot(1-0.333))}{144}\right) \\ &\sim & N(0.333,0.00154) \end{eqnarray*}\]
\[\begin{eqnarray*} P(\hat\pi > 0.35) &=& P\left( \frac {\hat\pi - \pi}{\sqrt{\pi(1-\pi)/n}} > \frac {0.35 - 0.333}{\sqrt{0.002}} \right) \\ &=& P\left( Z > 0.42\right) \\ &=& 1-P(Z< 0.42 )\\ &=& 1-\Phi( 0.42 ) \\ &=& 0.3372 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(\hat \lambda\) lo stimatore di massima verosimiglianza di \(\lambda\) del modello di Poisson: \(\hat\lambda = \frac 1n\sum_{i=1}^nx_i\) Scrivere la Varianza di \(\hat \lambda\).
4.b (Punti 3) Se \(h\) è uno stimatore per \(\theta\) tale che \(E(h)\ne \theta\) e che \(\lim_ {n\to +\infty}V(h)=0\) di quale proprietà gode \(h\)?
4.c (Punti 3) Definire gli errori di primo e di secondo tipo di un test statistico e le relative probabilità.
4.d (Punti 3) In un confronto tra due campioni viene messo a test \[ \begin{cases} H_0:\sigma_A=\sigma_B\\ H_1:\sigma_A\ne \sigma_B \end{cases} \] Risulta \(p_\text{value}=0.002\). Alla luce di questo risultato, per testare la differenza tra le medie, cosa è preferibile, un test sotto ipotesi di omogeneità, oppure sotto ipotesi di eterogeneità? Perché?
Esercizio 5
(Punti 14) In uno studio sule preferenze di genere è stato chiesto ad un campione di 150 persone, divise 80 signori e 70 signore, di esprimere la propria preferenza tra tre profumazioni (A, B e C) di shampoo. Qui di seguita la tavola di contingenza
| A | B | C | Tot | |
|---|---|---|---|---|
| M | 50 | 10 | 20 | 80 |
| F | 5 | 55 | 10 | 70 |
| Tot | 55 | 65 | 30 | 150 |
Testare al 5% l’ipotesi che vi sia indipendenza tra genere e preferenza tra le profumazioni.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[ \Big\{H_0:\pi_{ij}=\pi_{i\bullet}\pi_{\bullet j} \]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(\chi^2\)
Si usa il test \(\chi^2\), si crea la tabella delle frequenze teoriche \[ n_{ij}^*=\frac{n_{i\bullet}n_{\bullet j}}{n} \]
| A | B | C | Tot | |
|---|---|---|---|---|
| M | 29.3 | 34.7 | 16 | 80 |
| F | 25.7 | 30.3 | 14 | 70 |
| Tot | 55.0 | 65.0 | 30 | 150 |
La tabella delle distanze \[ \frac{(n_{ij}-n_{ij}^*)^2}{n_{ij}^*} \]
| A | B | C | Tot | |
|---|---|---|---|---|
| M | 14.6 | 17.6 | 1.00 | 0 |
| F | 16.6 | 20.1 | 1.14 | 0 |
| Tot | 0.0 | 0.0 | 0.00 | 0 |
\(\fbox{C}\) DECISIONE
\[ \chi^2_{obs}=70.954 \]
i \(gdl\)
\[ (3-1)\times(4-1)=6 \]
\(\alpha=0.01\) e quindi \(\chi_{1,0.01}^2=16.812\)
Essendo \[ \chi^2_{obs}=70.954 >\chi_{1,0.01}^2=16.812 \]
allora rifiuto \(H_0\) al lds dell’1 percento.
Graficamente
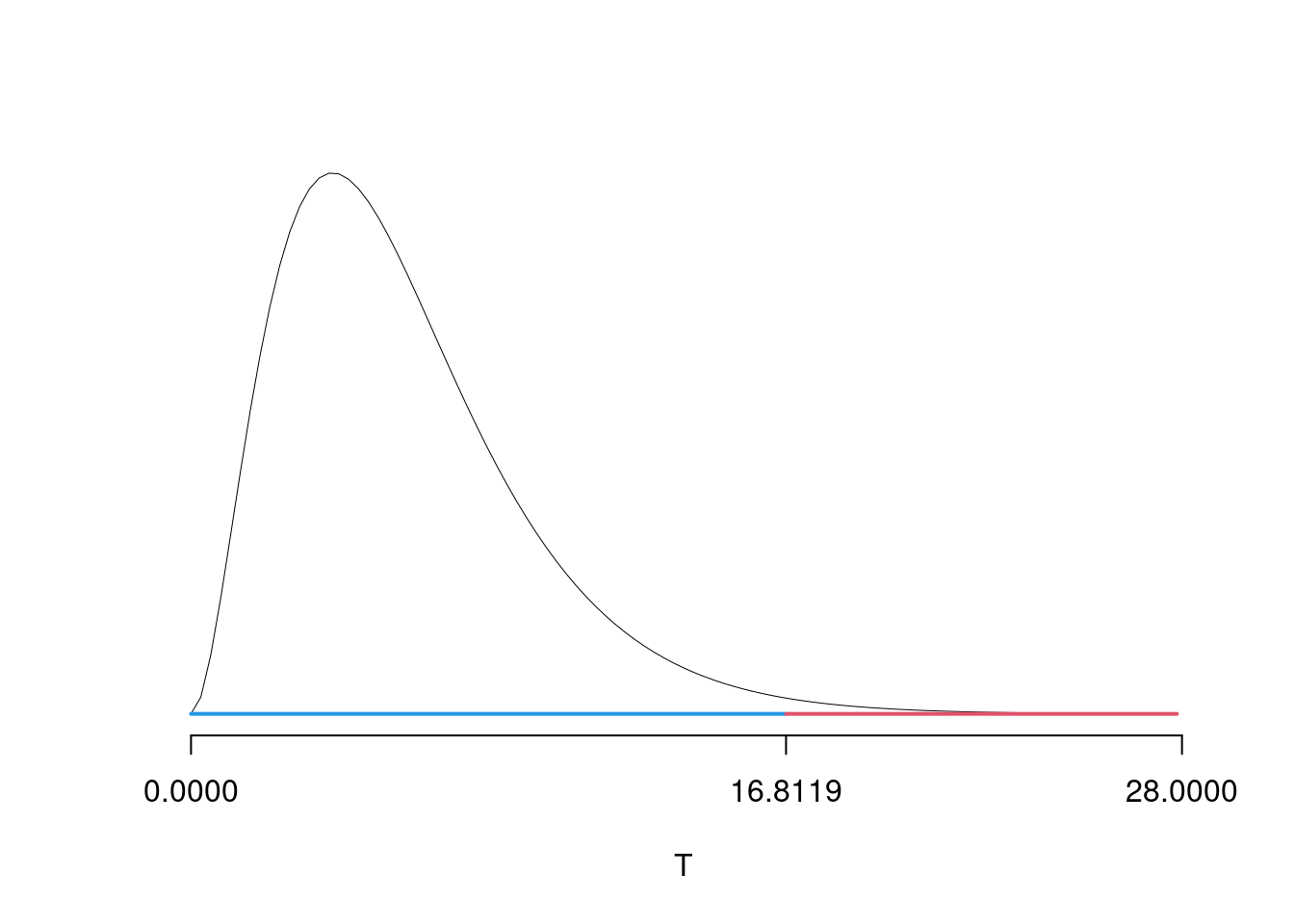
Il \(p_{\text{value}}\) è \[ P(\chi^2_{6}> \chi^2_{\text{obs}})=2.606e-13 \]
Esercizio 6
Sono stati analizzati 5 comuni della provincia di Bologna e su ogni comune è stato rilevato il PIL pro capite del comune \(X\), espresso in decine di migliaia di euro e un valore di percezione di qualità della vita \(Y\) (espresso su opportuna scala).
Qui di seguito i dati
| A | B | C | D | E | |
|---|---|---|---|---|---|
| \(x_i\) | 0.4 | 1.0 | 1.3 | 2.7 | 3.1 |
| \(y_i\) | 3.2 | 6.8 | 5.0 | 6.9 | 6.3 |
6.a (Punti 14) Calcolare il residuo del comune B nel modello di regressione dove \(Y\) viene spiegata da \(X\).
| \(i\) | \(x_i\) | \(y_i\) | \(x_i^2\) | \(y_i^2\) | \(x_i\cdot y_i\) |
|---|---|---|---|---|---|
| 1 | 0.4 | 3.20 | 0.16 | 10.2 | 1.28 |
| 2 | 1.0 | 6.80 | 1.00 | 46.2 | 6.80 |
| 3 | 1.3 | 5.00 | 1.69 | 25.0 | 6.50 |
| 4 | 2.7 | 6.90 | 7.29 | 47.6 | 18.63 |
| 5 | 3.1 | 6.30 | 9.61 | 39.7 | 19.53 |
| Totale | 8.5 | 28.20 | 19.75 | 168.8 | 52.74 |
| Totale/n | 1.7 | 5.64 | 3.95 | 33.8 | 10.55 |
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{5} 8.5= 1.7\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{5} 28.2= 5.64\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{5} 19.75 -1.7^2=0.222\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{5} 168.78 -5.64^2=1.946\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{5} 52.74-1.7\cdot5.64=0.96\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{0.96}{0.222} = 0.906\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 5.64-0.9057\times 1.7=4.1 \end{eqnarray*}\]
\[\begin{eqnarray*} \hat y_i &=&\hat\beta_0+\hat\beta_1 x_i=\\ &=& 4.1 + 0.9057 \times 1 = 5.01 \\ \hat \varepsilon_i &=& y_i-\hat y_i\\ &=& 6.8 - 5.01 = 1.79 \end{eqnarray*}\]
6.b (Punti 3) Scrivere la scomposizione della varianza del modello di regressione e calcolare la Total Sum of Squares (TSS), la Explained Sum of Squares (ESS) e la Residual Sum of Squares (RSS) dei dati analizzati sopra.
\[\begin{eqnarray*} TSS &=& n\hat\sigma^2_Y\\ &=& 5 \times 1.95 \\ &=& 9.73 \\ ESS &=& R^2\cdot TSS\\ &=& 0.447 \cdot 9.73 \\ &=& 4.35 \\ RSS &=& (1-R^2)\cdot TSS\\ &=& (1- 0.447 )\cdot 9.73 \\ &=& 5.38 \\ TSS &=& RSS+TSS \\ 9.73 &=& 4.35 + 5.38 \end{eqnarray*}\]
6.c (Punti 3) Interpretare il parametro di regressione \(\hat\beta_1\).
6.d (Punti 2) Descrivere la differenza tra punti di leva e punti influenti.
6.e (Punti 2) Gli stimatori \(\hat\beta_0\) e \(\hat\beta_1\) dei minimi quadrati per \(\beta_0\) e \(\beta_1\) sono corretti?
Prova di Statistica 2022/07/27-2
Esercizio 1
Su un campione di \(220\) imprese della provincia di Milano è stato rilevato il bilancio, espresso in migliaia di euro, del 2020. Qui di seguito i dati raccolti in classi e le frequenze cumulate.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(F_j\) |
|---|---|---|
| -10 | -5 | 0.036 |
| -5 | 0 | 0.305 |
| 0 | 2 | 0.768 |
| 2 | 4 | 0.923 |
| 4 | 6 | 1.000 |
1.a (Punti 14) Disegnare l’istogramma delle densità percentuali.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|
| -10 | -5 | 8 | 0.036 | 5 | 0.727 | 0.036 |
| -5 | 0 | 59 | 0.268 | 5 | 5.364 | 0.305 |
| 0 | 2 | 102 | 0.464 | 2 | 23.182 | 0.768 |
| 2 | 4 | 34 | 0.155 | 2 | 7.727 | 0.923 |
| 4 | 6 | 17 | 0.077 | 2 | 3.864 | 1.000 |
| 220 | 1.000 | 16 |
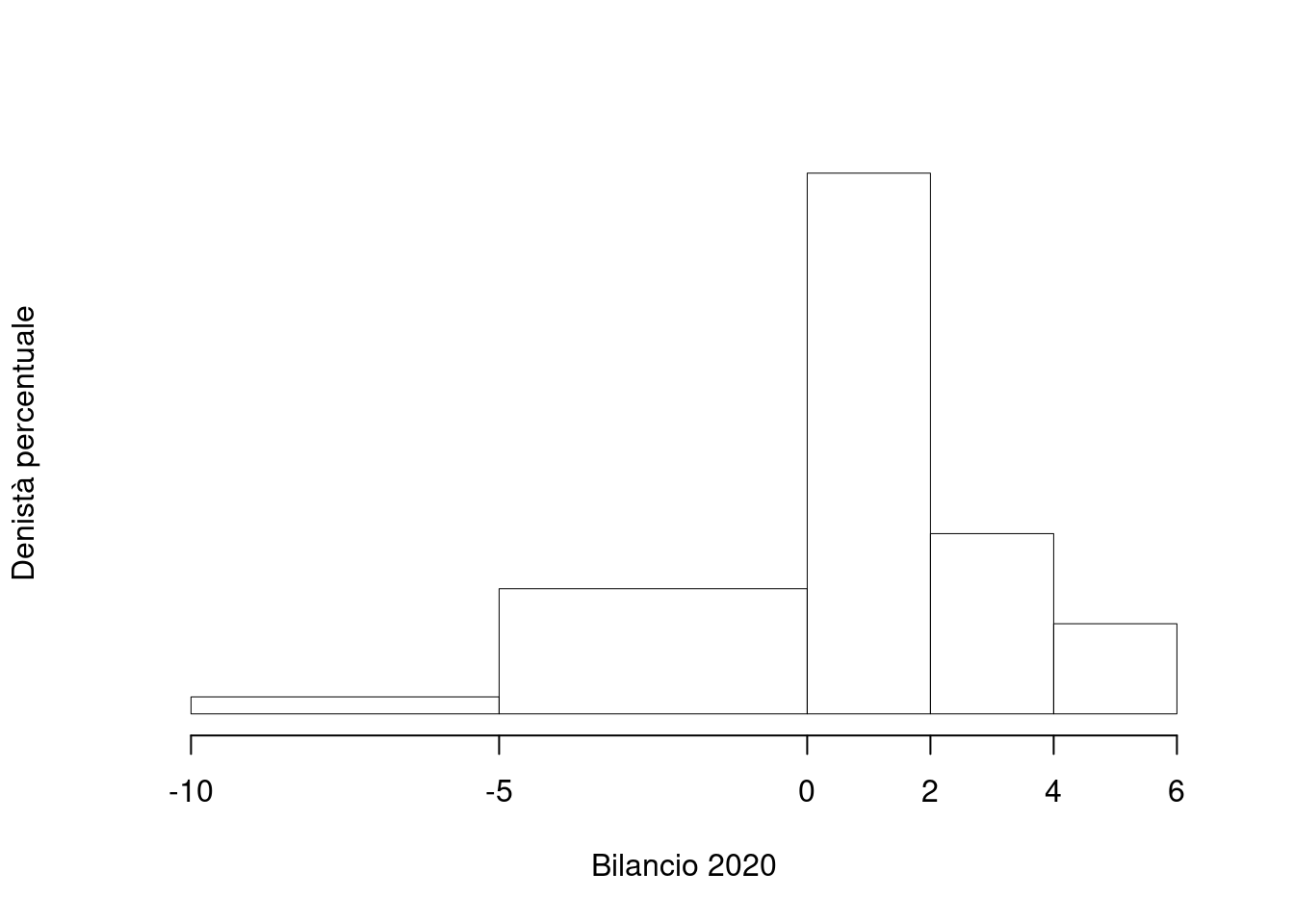
1.b (Punti 3) Quante aziende hanno un bilancio compreso tra il 25-esimo percentile e 3.5 mila euro?
\[\#(x_{0.25}<X<0)=n(F(3.5)-0.25)=220(0.884-0.25)=139.5\]
1.c (Punti 2) Che relazione dobbiamo attenderci tra media, mediana e moda?
\[\bar x<x_{0.5}<x_{Mo}\]
1.d (Punti 2) Siano \(x_1,...,x_n\), \(n\) numeri. Si consideri la funzione: \[g(x)=(x_1-x)^2+...+(x_n-x)^2.\] Per quale valore di \(x\), \(g(x)\) è minima?
Esercizio 2
In una strada, in prossimità di un dato incrocio, ci sono 3 corsie. In orario di punta, il numero di automobili che impegna la corsia sinistra è descritto da una Poisson di parametro 1.1, \(X_S\sim\text{Pois}(1.1)\), per quella di centro da una Poisson di parametro 1.0, \(X_C\sim\text{Pois}(1.0)\) e per quella di destra da una Poisson di parametro 0.9, \(X_D\sim\text{Pois}(0.9)\). Si assume l’indipendenza tra le variabili.
2.a (Punti 14) Si consideri l’evento \(E\)=“più di due veicoli impegnano l’incrocio”. Calcolare \(P(E)\).
Posto \(X=X_S+X_C+X_D\) osserviamo che \[X\sim\text{Pois}(\lambda=1.1+0.9+1)\] e quindi \[P(X\ge 2)=1-P(X\le 1)=1-(0.05+0.149)=0.801\]
2.b (Punti 3) Calcolare \[ P(X_S+X_C+X_D=3|X_S+X_C+X_D\ge 2). \]
Posto \(X=X_S+X_C+X_D\) osserviamo che \[\{X=3\}\cap\{X \ge 2\}=\{X=3\}\] e quindi \[\begin{eqnarray*} P(X=3|X\ge 2) &=& \frac{P(\{X=3\}\cap\{X \ge 2\})}{P(X \ge 2)}\\ &=&\frac{P(X=3)}{P(X \ge 2)}\\ &=&\frac{0.224}{0.801}=0.28\\ \end{eqnarray*}\]
2.c (Punti 2) Siano \(X\sim N(0,1)\) e \(Y\sim N(0,1)\), \(X\) e \(Y\) indipendenti. Come si distribuisce \(X^2+Y^2\)?
2.d (Punti 2) Se \(X\) è una VC con supporto {2,3,4,5} e \(Y\) è una VC con supporto {1,2,6}. Qual è il supporto di \(X-Y\)?
\(S_{X-Y}=-4, -3, -2, -1, 0, 1, 2, 3, 4\)
Esercizio 3
(Punti 14) Un’urna contiene 4 palline numerate da 1 a 4. Si estrae 100 volte con reinserimento e si fa la media dei 100 numeri estratti. Qual è la probabilità che la media sia compresa tra 2.5 e 2.6?
\[\begin{eqnarray*} \mu &=& E(X_i) = \sum_{x\in S_X}x P(X=x)\\ &=& 1 \frac { 1 }{ 4 }+ 2 \frac { 1 }{ 4 }+ 3 \frac { 1 }{ 4 }+ 4 \frac { 1 }{ 4 } \\ &=& 2.5 \\ \sigma^2 &=& V(X_i) = \sum_{x\in S_X}x^2 P(X=x)-\mu^2\\ &=&\left( 1 ^2\frac { 1 }{ 4 }+ 2 ^2\frac { 1 }{ 4 }+ 3 ^2\frac { 1 }{ 4 }+ 4 ^2\frac { 1 }{ 4 } \right)-( 2.5 )^2\\ &=& 1.25 \end{eqnarray*}\] Teorema del Limite Centrale (media VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=100\) VC IID, tc \(E(X_i)=\mu=2.5\) e \(V(X_i)=\sigma^2=1.25,\forall i\), posto: \[ \bar X=\frac{S_n}n =\frac{X_1 + ... + X_n}n \] allora:\[\begin{eqnarray*} \bar X & \mathop{\sim}\limits_{a}& N(\mu,\sigma^2/n) \\ &\sim & N\left(2.5,\frac{1.25}{100}\right) \\ &\sim & N(2.5,0.0125) \end{eqnarray*}\]
\[\begin{eqnarray*} P(2.5<\bar X\leq 2.6) &=& P\left( \frac {2.5 - 2.5}{\sqrt{0.013}} < \frac {\bar X - \mu}{\sqrt{\sigma^2/n}} \leq \frac {2.6 - 2.5}{\sqrt{0.013}}\right) \\ &=& P\left( 0 < Z \leq 0.89\right) \\ &=& \Phi(0.89)-\Phi(0)\\ &=& 0.8133 - 0.5 \\ &=& 0.313 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Siano \(h_1\) e \(h_2\) due stimatori per \(\theta\), tali che
\[ MSE(h_1) = \frac{\theta}{\sqrt{n}}, \qquad MSE(h_2) = \frac{\theta}{n} \]
Quale dei due stimatori è più efficiente?
4.b (Punti 3) Sia \(\hat\sigma^2\) lo stimatore di massima verosimiglianza di \(\sigma^2\). In virtù di quale proprietà \(\hat \sigma\) è lo stimatore di massima verosimiglianza per \(\sigma\)?
4.c (Punti 3) Siano \(T_1\) e \(T_2\) due test per lo stesso sistema di ipotesi, con uguale significatività \(\alpha=0.05\) e con probabilità di errore di secondo tipo, \(\beta_1=0.3\) per il test \(T_1\) e \(\beta_2=0.15\) per il test \(T_2\). Quale dei due test è più potente?
4.d (Punti 3) Se in un test statistico bilaterale che utilizza la statistica test t con 11 gradi di libertà, \(t_\text{obs}=142.3\), il \(p_\text{value}\) sarà maggiore o minore di 0.01? Perché?
Esercizio 5
Su un campione di \(n_M=35\) consumatori privati, scelti a caso tra i cittadini del comune di Modena, si è chiesto quanto spendono mensilmente per le forniture elettriche. Il campione ha restituito una media pari a 12.4 €/mese, con una deviazione standard pari a 2.1 €/mese,
(Punti 4) Costruire un Intervallo di Confidenza al 95% per la media di popolazione \(\mu\).
\[ S=\sqrt{\frac{n}{n-1}}\hat \sigma=2.131 \]
\[\begin{eqnarray*} \left[~~12.4\pm t_{34;.005}{\frac{2.131}{\sqrt{35}}}~~\right] &=& \left[~~12.4\pm 2.728\times0.36~~\right]\\ &=&\left[~~11.417; 13.383~~\right] \end{eqnarray*}\]
(Punti 10) La stessa domanda è stata posta ad un secondo campione di \(n_F=38\) consumatori privati,scelti a caso tra i cittadini del comune di Ferrara. Il campione ha restituito una media pari a 19.2 €/mese, con una deviazione standard pari a 3.9 €/mese. Sotto ipotesi di eterogeneità testare al 5% l’ipotesi che i due comuni abbiano uguale media, contro l’alternativa che a Ferrara consumino di più.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0:\mu_\text{1} = \mu_\text{ 2}\text{}\\ H_1:\mu_\text{1} < \mu_\text{ 2}\text{} \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(T\)
L’ipotesi è di eterogeneità e quindi calcoliamo: \[ S^2_\text{1}=\frac{n_\text{1}}{n_\text{1}-1}\hat\sigma^2_\text{1}=\frac{35}{35-1}2.1^2=4.54 \qquad S^2_\text{2}=\frac{n_\text{2}}{n_\text{2}-1}\hat\sigma^2_\text{2}=\frac{38}{38-1}3.9^2=15.621 \]
\[\begin{eqnarray*} \frac{\hat\mu_\text{1} - \hat\mu_\text{2}} {\sqrt{\frac {S^2_\text{1}}{n_\text{1}}+\frac {S^2_\text{2}}{n_\text{2}}}}&\sim&t_{n_\text{1}+n_\text{2}-2}\\ t_{\text{obs}} &=& \frac{ (12.4- 19.2)} {\sqrt{\frac{4.54}{35}+\frac{15.621}{38}}} = -9.247\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE
Dalle tavole si ha \(t_{(35+38-2);\, 0.05} = -1.667\). \[t_{\text{obs}} = -9.247 < t_{71;\, 0.05} = -1.667\]
CONCLUSIONE: i dati non sono coerenti con \(H_{0}\) al LdS del 5%
Graficamente
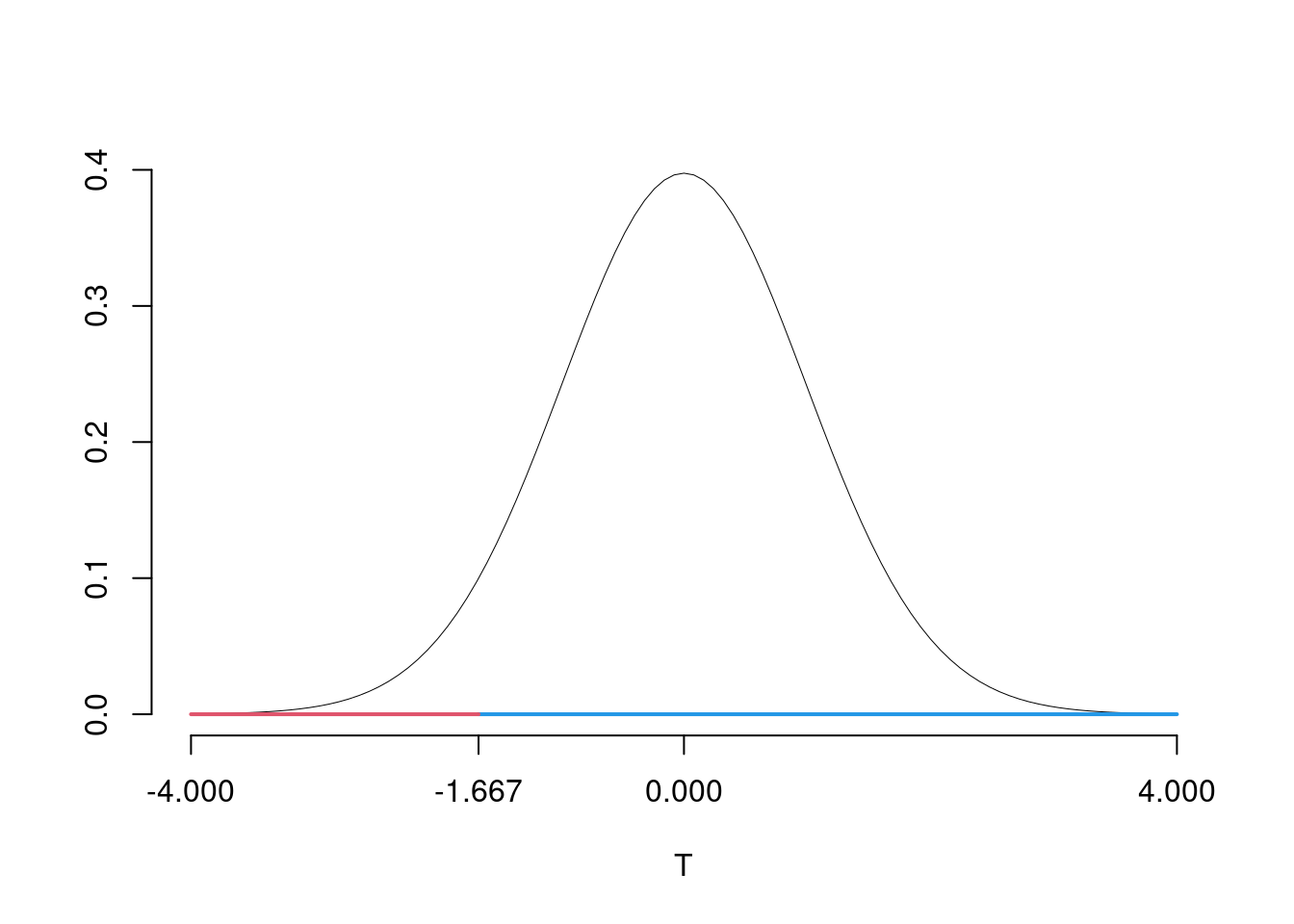
Il \(p_{\text{value}}\) è \[P(T_{n1+n2-2}<t_{\text{obs}})=P(T_{n1+n2-2}< -9.247 )= 4.113e-14\]
Esercizio 6
Sono stati analizzati 15 comuni della provincia di Bologna e su ogni comune è stato rilevato il PIL pro capite del comune \(X\), espresso in decine di migliaia di euro e un valore di percezione di qualità della vita \(Y\) (espresso su opportuna scala).
Qui di seguito le statistiche bivariate
\[\begin{align*} \sum_{i=1}^n x_i &= 29.3 &\sum_{i=1}^n x_i^2 &= 74.51 &\sum_{i=1}^n x_i y_i &= 242.81\\ \sum_{i=1}^n y_i &= 110.8 & \sum_{i=1}^n y_i^2 &= 866.02 & \end{align*}\]
6.a (Punti 14) Stimare la previsione per \(x=1.6\) nel modello di regressione dove \(Y\) viene spiegata da \(X\).
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{15} 29.3= 1.953\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{15} 110.8= 7.387\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{15} 74.51 -1.9533^2=1.25\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{15} 866.02 -7.3867^2=3.172\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{15} 242.81-1.9533\cdot7.3867=1.759\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{1.759}{1.25} = 1.527\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 7.387-1.5269\times 1.9533=4.404 \end{eqnarray*}\]
\[\hat y_{X= 1.6 }=\hat\beta_0+\hat\beta_1 x= 4.4 + 1.5269 \times 1.6 = 6.85 \]
6.b (Punti 3) Calcolare numericamente \(RSS\): \[ RSS=\sum_{i=1}^n \hat\epsilon_i^2 \]
\[RSS=n(1-r^2)\hat\sigma_Y^2=7.297\]
6.c (Punti 3) Gli stimatori \(\hat\beta_0\) e \(\hat\beta_1\) sono consistenti? Perché?
6.d (Punti 2) Se in un modello di regressione con 11 dati, il residuo studentizzato del dato \(i\) è \(\tilde \epsilon_i=1.23\), cosa possiamo concludere?
6.e (Punti 2) Sia \(\hat\beta_1\) lo stimatore dei minimi quadrati per \(\beta_1\). Scrivere il suo Standard Error teorico.
Prova di Statistica 2022/07/27-3
Esercizio 1
Su un campione di \(220\) imprese della provincia di Milano è stato rilevato il bilancio, espresso in migliaia di euro, del 2020. Qui di seguito i dati raccolti in classi e le densità di frequenza percentuale.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(h_j\) |
|---|---|---|
| -10 | -5 | 0.909 |
| -5 | 0 | 3.455 |
| 0 | 2 | 26.136 |
| 2 | 4 | 8.636 |
| 4 | 6 | 4.318 |
1.a (Punti 14) Calcolare il valore approssimato della mediana.
| \([\text{x}_j,\) | \(\text{x}_{j+1})\) | \(n_j\) | \(f_j\) | \(b_j\) | \(h_j\) | \(F_j\) |
|---|---|---|---|---|---|---|
| -10 | -5 | 10 | 0.045 | 5 | 0.909 | 0.045 |
| -5 | 0 | 38 | 0.173 | 5 | 3.455 | 0.218 |
| 0 | 2 | 115 | 0.523 | 2 | 26.136 | 0.741 |
| 2 | 4 | 38 | 0.173 | 2 | 8.636 | 0.914 |
| 4 | 6 | 19 | 0.086 | 2 | 4.318 | 1.000 |
| 220 | 1.000 | 16 |
\[\begin{eqnarray*} p &=& 0.5, \text{essendo }F_{3}=0.741 >0.5 \Rightarrow j_{0.5}=3\\ x_{0.5} &=& x_{\text{inf};3} + \frac{ {0.5} - F_{2}} {f_{3}} \cdot b_{3} \\ &=& 0 + \frac {{0.5} - 0.218} {0.523} \cdot 2 \\ &=& 1.078 \end{eqnarray*}\]
1.b (Punti 3) Quante aziende hanno un bilancio compreso tra \(-1\) e il 75-esimo percentile?
\[\begin{eqnarray*} F(x_{0.75}) &=& 0.75\\ F(-1) &=& f_1+4h_2/100\\ &=& 0.045+4\times 3.455/100\\ &=& 0.184\\ \%(-1<X<x_{0.75}) &=& (F(x_{0.75})-F(x_{-1}))\times 100\\ &=& (0.566)\times 100 \%\\ \#(-1<X<x_{0.75}) &=& n\%(-1<X<x_{0.75})/100 \\ &=& 124.6 \end{eqnarray*}\]
\[ \#(-1<X<x_{0.75})=n\%(-1<X<x_{0.75})/100=n/100(75-F(-1)) \]
1.c (Punti 2) Che relazione dobbiamo attenderci tra media, mediana e moda?
1.d (Punti 2) Sapendo che \(\sigma_X=2.82\) la Standard Deviation di \(X\) e posto \(y_i=-x_i, \forall i\), quanto varrà \(\sigma_Y\), la standard deviation dei dati così trasformati?
Esercizio 2
Una moneta perfetta viene lanciata 2 volte, se esce almeno 1 volta testa si estrae da un’urna che contiene un biglietto vincente ed uno perdente, altrimenti si estrae da un’urna che contiene due biglietti vincenti e tre perdenti.
2.a (Punti 14) Qual è la probabilità di vincere?
Sia \(X\sim\text{Binom}(1/2)\) \[P(E)=P(X\ge 1)=1-P(X=0)=1-\frac 14=\frac 34\]
\[\begin{eqnarray*} P(Vincere) &=& P(E)P(Vincere|E)+P(\bar E)P(Vincere|\bar E)\\ &=& \frac 34\frac 12 + \frac 14 \frac 23\\ &=& 0.542 \end{eqnarray*}\]
2.b (Punti 3) Si ripete il gioco di sopra finché non si vince tre volte. Qual è la probabilità di finire alla quinta giocata?
\[\begin{eqnarray*} P(\text{Finire alla quarta}) &=& P(\text{Vincere 2 partite su 3}\cap\text{vincere alla quarta})\\ &=& \left(\binom{3}{2}0.542^2(1-0.542)^1\right)\times 0.542\\ &=& 0.403\times 0.542\\ &=& 0.219 \end{eqnarray*}\]
2.c (Punti 2) Se \(X\) è una VC con supporto {1,2,3} e \(Y\) è una VC con supporto {1,3,5}. Qual è il supporto di \(X\times Y\)?
\[S_{X-Y}=1, 2, 3, 5, 6, 9, 10, 15\]
Esercizio 3
(Punti 14) Il supermercato S accoglie, in media ogni giorno, 3.242 mila persone, con una deviazione standard di 0.5 mila persone. Dopo 60 giorni di apertura, qual è la probabilità che il totale dei visitatori sia maggiore di 225 mila persone?
Teorema del Limite Centrale (somma VC qualunque)
Siano \(X_1\),…,\(X_n\), \(n=60\) VC IID, tc \(E(X_i)=\mu=3.24\) e \(V(X_i)=\sigma^2=0.25,\forall i\), posto: \[ S_n = X_1 + ... + X_n \] allora:\[\begin{eqnarray*} S_n & \mathop{\sim}\limits_{a}& N(n\mu,n\sigma^2) \\ &\sim & N(60\cdot3.24,60\cdot0.25) \\ &\sim & N(195,15) \end{eqnarray*}\]
\[\begin{eqnarray*} P(S_n > 225) &=& P\left( \frac {S_n - n\mu}{\sqrt{n\sigma^2}} > \frac {225 - 194.52}{\sqrt{15}} \right) \\ &=& P\left( Z > 7.87\right) \\ &=& 1-P(Z< 7.87 )\\ &=& 1-\Phi( 7.87 ) \\ &=& 0 \end{eqnarray*}\]
Esercizio 4
4.a (Punti 3) Sia \(h\) uno stimatore per \(\theta\), tale che
\[ MSE(h) = \theta+\frac{\theta}{n^2} \]
Lo stimatore \(h\) è consistente?
4.b (Punti 3) Sia \(\hat\theta\) lo stimatore di massima verosimiglianza per \(\theta\). Qual è la distribuzione asintotica di \(\hat\theta\)?
4.c (Punti 3) Un intervallo di confidenza per \(\theta\) al 90% è più ampio o meno ampio di uno al 95%? Perché?
4.d (Punti 3) Se in un test statistico bilaterale che utilizza la statistica test z , risulta \(z_\text{obs}=14\), il \(p_\text{value}\) sarà maggiore o minore di 0.01? Perché?
Esercizio 5
Su un campione di \(n_R=75\) tassisti romani è stato chiesto se siano favorevoli o meno all’introduzione del decreto di liberalizzazione del trasporto. Lo studio ha riportato che 15 persone su 75 (l’20% del campione) è favorevole.
5.a (Punti 4) Costruire un intervallo di confidenza la 95% per \(\pi\) la quota di tassisti favorevoli al decreto liberalizzazione
\[\begin{eqnarray*} \left[~~0.2\pm z_{0.025}\sqrt{\frac{0.2\times 0.8}{75}}~~\right] &=& \left[~~0.2\pm 1.96\times0.046~~\right]\\ &=&\left[~~0.109; 0.291~~\right] \end{eqnarray*}\]
5.b (Punti 10) La stessa domanda è stata posta ad un secondo campione di \(n_M=95\) tassisti milanesi. Lo studio ha riportato che 32 persone su 95 (l’20% del campione) è favorevole.
Testare al 5% l’ipotesi la quota di tassisti favorevoli sia uguale tra le due città contro l’alternativa che i tassisti milanesi siano maggiormente favorevoli.
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI \[\begin{cases} H_0:\pi_\text{$R$} = \pi_\text{ $M$}\text{}\\ H_1:\pi_\text{$R$} < \pi_\text{ $M$}\text{} \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)
\[\hat\pi_\text{$R$}=\frac{s_\text{$R$}}{n_\text{$R$}}=\frac{15}{75}=0.2\qquad \hat\pi_\text{$M$}=\frac{s_\text{$M$}}{n_\text{$M$}}=\frac{32}{95}=0.337\]
Calcoliamo la proporzione comune sotto \(H_0\) \[ \pi_C=\frac{s_\text{$R$}+s_\text{$M$}}{n_\text{$R$}+n_\text{$M$}}= \frac{47}{170}=0.276 \]
\[\begin{eqnarray*} \frac{\hat\pi_\text{$R$} - \hat\pi_\text{$M$}} {\sqrt{\frac {\pi_C(1-\pi_C)}{n_\text{$R$}}+\frac {\pi_C(1-\pi_C)}{n_\text{$M$}}}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ (0.2- 0.337)} {\sqrt{\frac{0.276(1-0.276)}{75}+\frac{0.276(1-0.276)}{95}}} = -1.981\, . \end{eqnarray*}\]
\(\fbox{C}\) DECISIONE Dalle tavole si ha \(z_{0.05} = -1.645\). \[z_{\text{obs}} = -1.981 < z_{0.05} = -1.645\]
CONCLUSIONE: i dati non sono coerenti con \(H_{0}\) al LdS del 5%
Graficamente
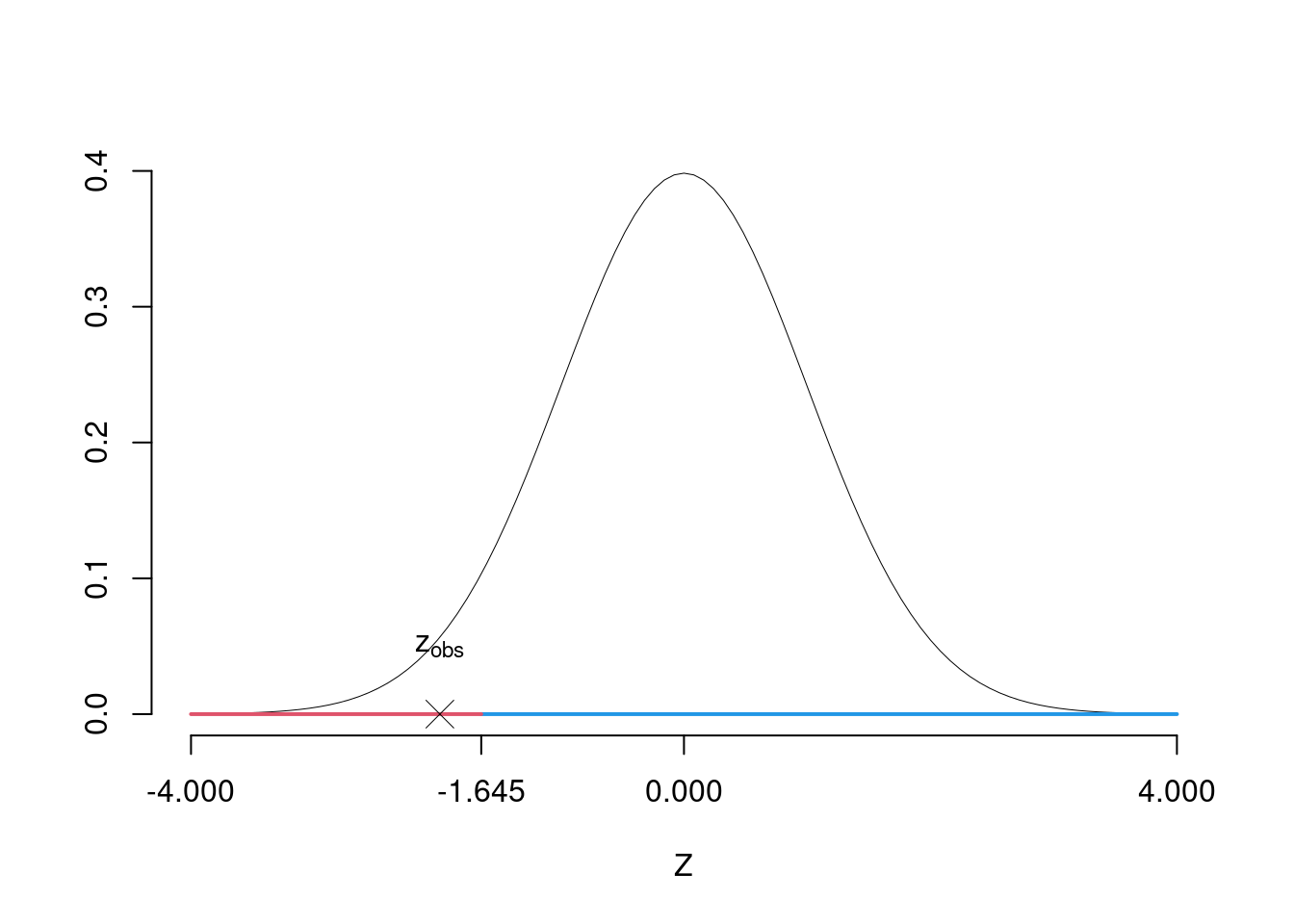
Il \(p_{\text{value}}\) è \[P(Z<z_{\text{obs}})=P(Z< -1.98 )= 0.02381\]
Esercizio 6
Sono stati analizzati 15 comuni della provincia di Bologna e su ogni comune è stato rilevato il PIL pro capite del comune \(X\), espresso in decine di migliaia di euro e un valore di percezione di qualità della vita \(Y\) (espresso su opportuna scala).
Qui di seguito le statistiche bivariate
\[\begin{align} \sum_{i=1}^n x_i &= 28.3 &\sum_{i=1}^n x_i^2 &= 71.19 &\sum_{i=1}^n x_i y_i &= 253.01\\ \sum_{i=1}^n y_i &= 122.2 & \sum_{i=1}^n y_i^2 &= 1042.2 & \end{align}\]
6.a (Punti 14) Questi sono alcuni dei dati osservati
| \(x_i\) | 2.5 | 2.1 | 0.3 | 3.0 |
| \(y_i\) | 6.7 | 9.3 | 6.0 | 9.5 |
Calcolare il residuo per \(x=2.1\) nel modello di regressione dove \(Y\) è spiegato da \(X\).
\[\begin{eqnarray*} \bar x &=&\frac 1 n\sum_{i=1}^n x_i = \frac {1}{15} 28.3= 1.887\\ \bar y &=&\frac 1 n\sum_{i=1}^n y_i = \frac {1}{15} 122.2= 8.147\\ \hat\sigma_X^2&=&\frac 1 n\sum_{i=1}^n x_i^2-\bar x^2=\frac {1}{15} 71.19 -1.8867^2=0.25\\ \hat\sigma_Y^2&=&\frac 1 n\sum_{i=1}^n y_i^2-\bar y^2=\frac {1}{15} 1042.2 -8.1467^2=3.112\\ \text{cov}(X,Y)&=&\frac 1 n\sum_{i=1}^n x_i~y_i-\bar x\bar y=\frac {1}{15} 253.01-1.8867\cdot8.1467=1.497\\ \hat\beta_1 &=& \frac{\text{cov}(X,Y)}{\hat\sigma_X^2} \\ &=& \frac{1.497}{0.25} = 1.262\\ \hat\beta_0 &=& \bar y - \hat\beta_1 \bar x\\ &=& 8.147-1.2619\times 1.8867=5.766 \end{eqnarray*}\]
\[\begin{eqnarray*} \hat y_i &=&\hat\beta_0+\hat\beta_1 x_i=\\ &=& 5.77 + 1.2619 \times 2.1 = 8.42 \\ \hat \varepsilon_i &=& y_i-\hat y_i\\ &=& 9.3 - 8.42 = 0.884 \end{eqnarray*}\]
6.b (Punti 3) Calcolare la percentuale di varianza di \(Y\) spiegata dal modello.
\[\begin{eqnarray*} r&=&\frac{\text{cov}(X,Y)}{\sigma_X\sigma_Y}=\frac{ 1.5 }{ 1.09 \times 1.76 }= 0.779 \\r^2&=& 0.607 < 0.75 \end{eqnarray*}\] Il modello non si adatta bene ai dati.
6.c (Punti 2) Se in un modello di regressione con 15 dati, il residuo studentizzato del dato \(i\) è \(\tilde \epsilon_i=12.3\), cosa possiamo concludere?
6.d (Punti 2) Sia \(\hat\beta_0\) lo stimatore dei minimi quadrati per \(\beta_0\). Scrivere il suo Standard Error stimato.