Capitolo 15 Test per una media e una proporzione
In questo capitolo svilupperemo il test per una media. Essendo la proporzione una particolare media su elementi 0 e 1 la costruzione verrà in automatico. In tutti i casi considereremo un solo campione \(x_1,...,x_n\) proveniente da una popolazione che ha media \(E(X_i)=\mu, \forall i\) e \(V(X_i)=\sigma^2, \forall i\).
Il sistema di ipotesi porrà sempre \(H_0:\mu=\mu_0\) e si leggerà: la vera media che ha generato i dati è \(\mu_0\), il fatto che la media dei dati sia \(\bar x\ne\mu_0\) è dovuto all’effetto del campionamento e la differenza tra \(\bar x\) e \(\mu_0\) non è significativa. L’ipotesi alternativa \(H_1\), che sarà unilaterale o bilaterale, si legge al contrario: la differenza tra la media osservata e la media prescritta da \(H_0\) è significativa e il campione proviene da una popolazione che non ha media \(\mu_0\).
Alla luce dei dati decideremo se scegliere di rifiutare \(H_0\) o se non rifiutarla. Costruiremo anche una misura di vicinanza empirica ad \(H_1\), il \(p_{\text{value}}\), che ci consentirà di capire quanto l’evidenza empirica dei dati supporti supporti una delle due ipotesi.
15.1 Test sulla media, \(\sigma^2\) noto
15.1.1 Test sulla media, ipotesi unilaterale destra, \(\sigma^2\) noto
Siano \(X_1,...X_n\), \(n\) VC, IID: \(X_i\sim N(\mu,\sigma^2)\) con \(\sigma^2\) noto. Consideriamo il seguente sistema di ipotesi
\[\begin{cases} H_0:\mu=\mu_0\\ H_1:\mu>\mu_0 \end{cases}\]
Dalle proprietà della normale
\[\hat\mu=\bar X=\frac 1 n\sum_{i=1}^nX_i\sim N\left(\mu,\frac{\sigma^2} {n}\right)\]
E quindi
\[Z=\frac{\hat\mu-\mu}{\sigma/\sqrt n}\sim N(0,1)\]
Sotto \(H_0: \mu=\mu_0\) la statistica
\[Z=\frac{\hat\mu-\mu_0}{\sigma/\sqrt n}\sim N(0,1)\]
\(Z\) osservata sul campione misura l’evidenza contro \(H_0\), tanto più è alto il valore di \(Z\) tanto più \(H_0\) è inverosimile.
Decisione sul campione. Si decide un livello \(\alpha\) e si ricava \(z_\alpha\), si estrae un campione. Lo stimatore \(\hat\mu\) si realizza nella media osservata del campione \(\bar x\)
\[z_{\text{obs}}=\frac{\bar x -\mu_0}{\sigma/\sqrt n}\]
- Se \(z_{\text{obs}}<z_\alpha\) \(H_0\) non viene rifiutata al livello di significatività \(\alpha\times100\%\)
- Se \(z_{\text{obs}}>z_\alpha\) \(H_0\) viene rifiutata al livello di significatività \(\alpha\times100\%\)
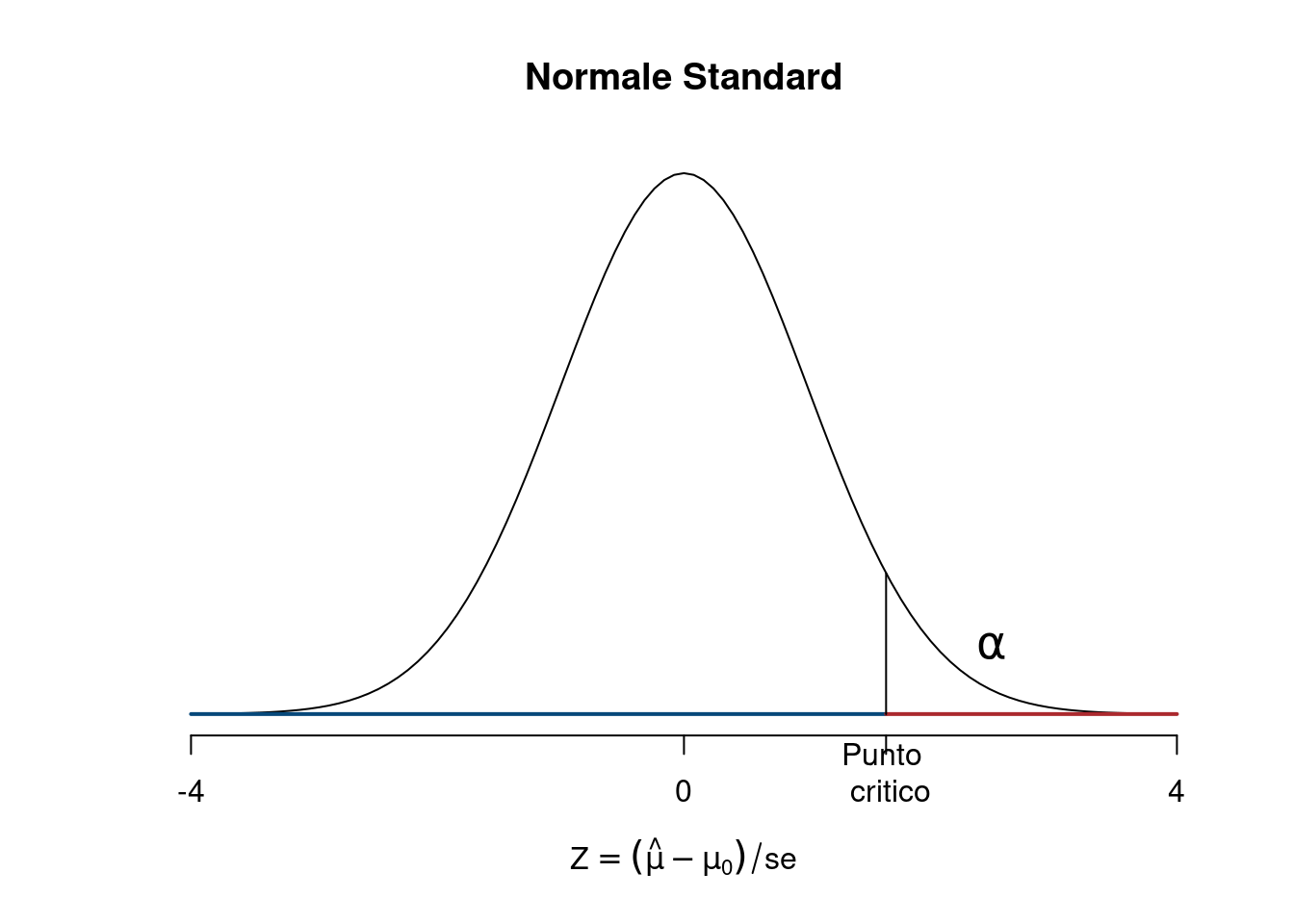
15.1.2 Test sulla media, \(\sigma^2\) noto, vari livelli di \(\alpha\)
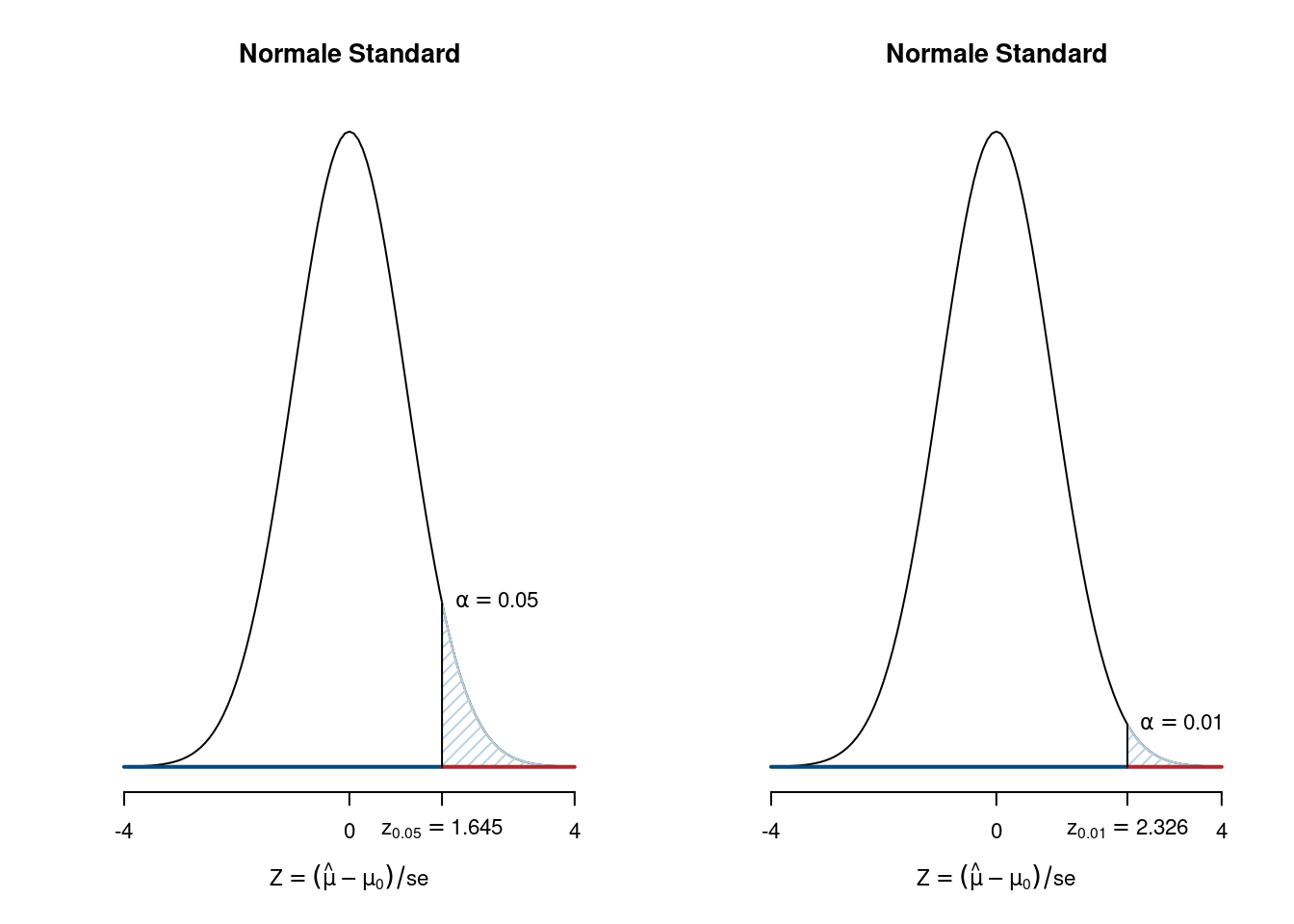
Se \(\alpha=0.05\) allora \[\text{Punto Critico}=z_{0.05},\qquad P(Z>z_{0.05})=0.05\] \(z_{0.05}=1.6449\)
Se \(\alpha=0.01\) allora \[\text{Punto Critico}=z_{0.01},\qquad P(Z>z_{0.01})=0.01\] \(z_{0.01}=2.3263\)
Esempio 15.1 In un laboratorio, vi sono cavie con peso medio uguale a 30g e una DS pari a 5g. Uno studente seleziona 25 cavie e ottiene un peso medio uguale a 32g con una \(\hat\sigma\) pari a 7g. La selezione è casuale o il valore ottenuto della media è troppo alto, a un LdS del 5%?
Test \(Z\) per una media, variazna nota
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \mu = \mu_0=30 \\ H_1: \mu > \mu_0=30 \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)
\(\sigma^{2}\) di \(\cal{P}\) è nota: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {\sigma/\sqrt{n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 32 - 30 )} { 5 /\sqrt{ 25 }} = 2 \, . \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
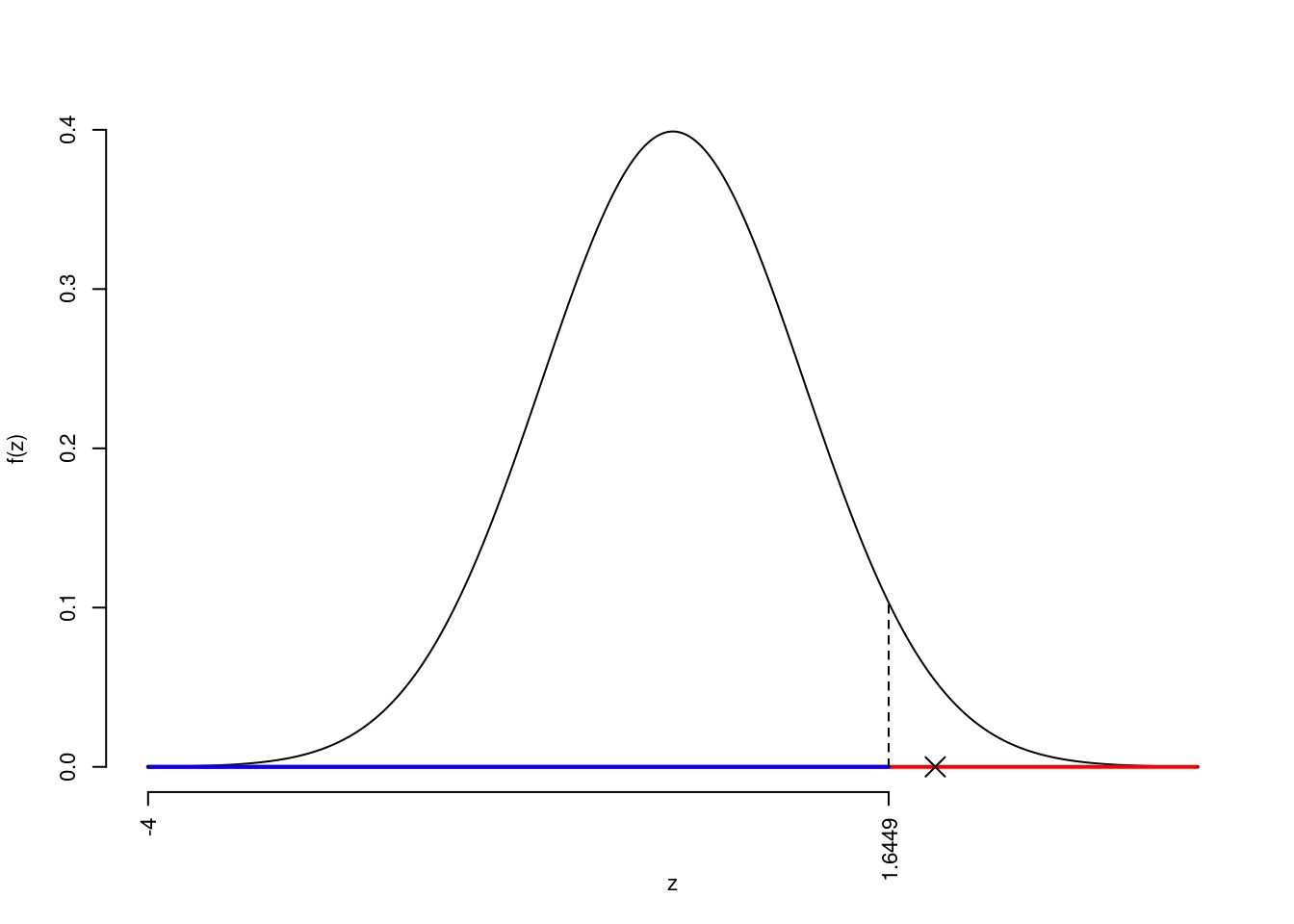
La siginficatitività è \(\alpha=0.05\), dalle tavole osserviamo \(z_{0.05}=1.6449\).
Essendo \(z_\text{obs}=2>z_{0.05}=1.6449\) allora rifiuto \(H_0\) al 5%.
Esempio 15.2 In un laboratorio, vi sono cavie con peso medio uguale a 30g e una DS pari a 5g. Uno studente seleziona 25 cavie e ottiene un peso medio uguale a 32g con una \(\hat\sigma\) pari a 7g. La selezione è casuale o il valore ottenuto della media è troppo alto, a un LdS del 1%?
Test \(Z\) per una media, variazna nota
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \mu = \mu_0=30g \\ H_1: \mu > \mu_0=30g \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)
\(\sigma^{2}\) di \(\cal{P}\) è nota: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {\sigma/\sqrt{n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 32 - 30 )} { 5 /\sqrt{ 25 }} = 2 \, . \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
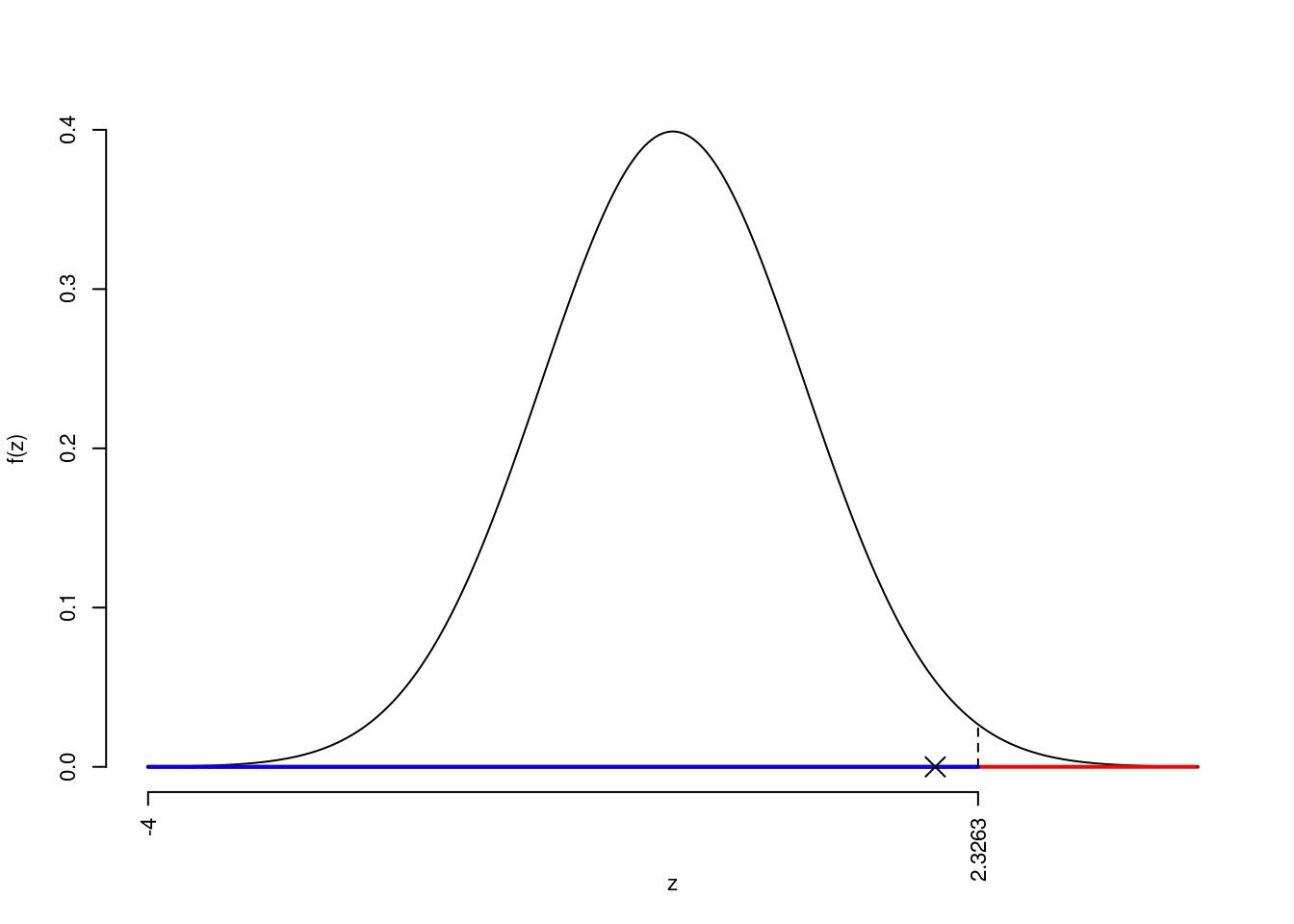
La siginficatitività è \(\alpha=0.01\), dalle tavole osserviamo \(z_{0.01}=2.3263\).
Essendo \(z_\text{obs}=2<z_{0.01}=2.3263\) allora non rifiuto \(H_0\) al 1%.
15.1.3 La probabilità di significatività osservata il \(p_\text{value}\)
Il \(p_\text{value}\) risponde a questa domanda: Se nell’esempio precedente usassimo \(z_{\text{obs}}\) come punto critico quale sarebbe la probabilità di significatività?
Definizione 15.1 ($p_\text{value}$ caso unilaterale destro) \[p_\text{value}=P(Z>z_{\text{obs}};H_0)\]
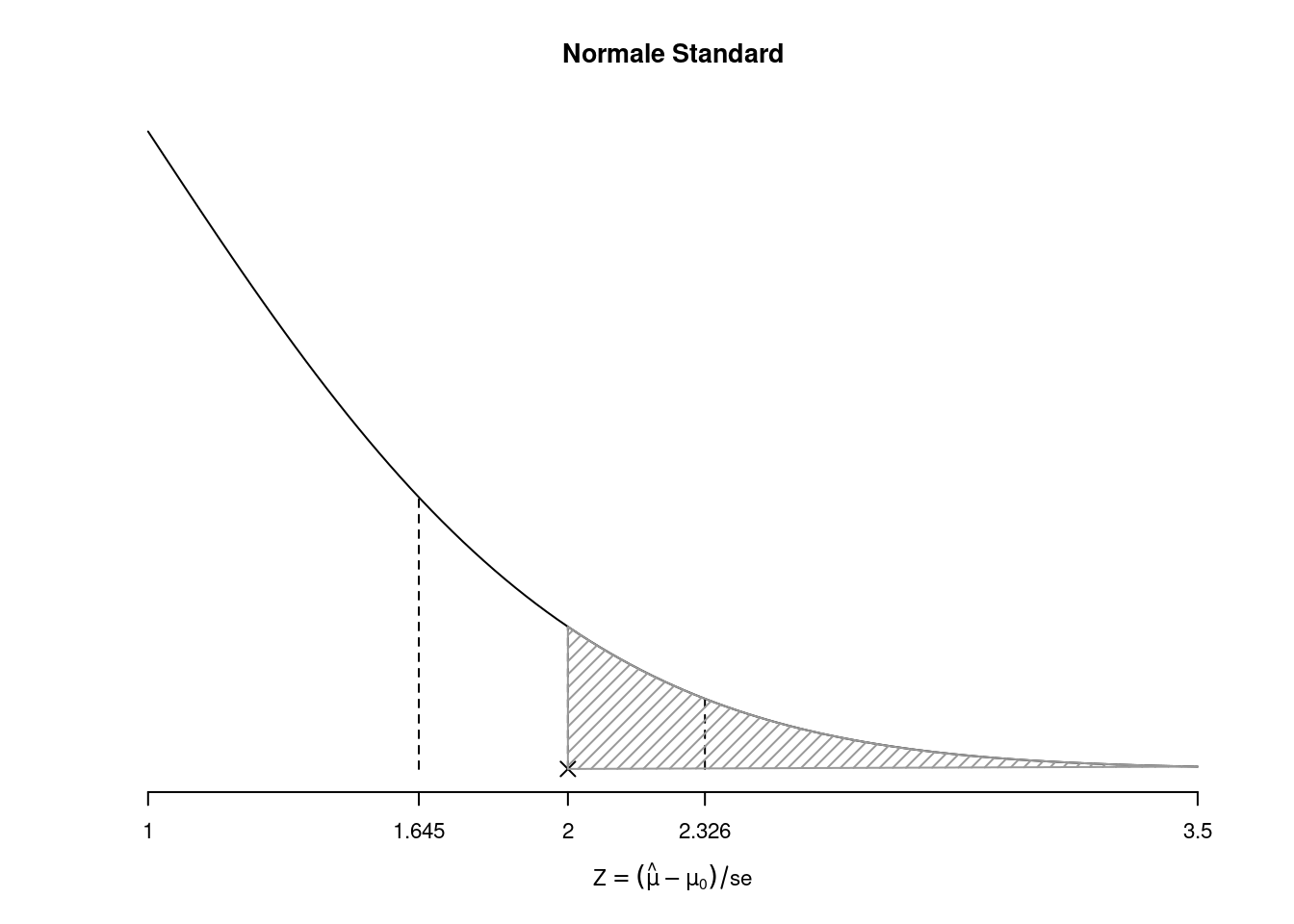
15.1.4 Lettura del \(p_\text{value}\)
La probabilità di significatività osservata \(p_\text{value}\) ci dice la probabilità, se fosse vera \(H_0\) di trovare un campione ancora più in favore di \(H_1\) di quello che ho trovato. In altre parole ci dice, se fosse vera \(H_0\), quanto sarebbe improbabile il nostro campione.
Tanto più basso è il \(p_\text{value}\) tanto più forte è l’evidenza dei dati contro \(H_0\):
- Se \(p_\text{value}>0.1\) \(\rightarrow\) il test non è significativo
- Se \(0.05< p_\text{value}\le 0.1\rightarrow\) il test è marginalmente significativo \(\fbox{.}\)
- Se \(0.05< p_\text{value}\le 0.01\rightarrow\) il test è significativo \(\rightarrow\) significativo al 5% \(\fbox{*}\)
- Se \(0.001< p_\text{value}\le 0.01\rightarrow\) il test è molto significativo \(\rightarrow\) significativo all’1% \(\fbox{**}\)
- Se \(p_\text{value}\le 0.001\rightarrow\) il test è estremamente significativo \(\rightarrow\) significativo sotto all’1‰ \(\fbox{***}\)
15.1.5 Test sulla media, ipotesi unilaterale sinistra, \(\sigma^2\) noto
Siano \(X_1,...X_n\) \(n\) VC, IID: \(X_i\sim N(\mu,\sigma^2)\) con \(\sigma^2\) noto.
Consideriamo il seguente sistema di ipotesi \[\begin{cases} H_0:\mu=\mu_0\\ H_1:\mu<\mu_0 \end{cases}\]
Dalle proprietà della normale \[\hat\mu=\bar X=\frac 1 n\sum_{i=1}^nX_i\sim N\left(\mu,\frac{\sigma^2} {n}\right)\]
E quindi \[Z=\frac{\hat\mu-\mu}{\sigma/\sqrt n}\sim N(0,1)\]
Sotto \(H_0\) la statistica \[Z=\frac{\hat\mu-\mu_0}{\sigma/\sqrt n}\sim N(0,1)\]
\(Z\) osservata sul campione misura l’evidenza contro \(H_0\), tanto più è basso il valore di \(Z\) tanto più \(H_0\) è inverosimile
Decisione sul campione. Si decide un livello \(\alpha\) e si ricava \(z_\alpha\), si estrae un campione. Lo stimatore \(\hat\mu\) si realizza nella media osservata del campione \(\bar x\)
\[z_{\text{obs}}=\frac{\bar x -\mu_0}{\sigma/\sqrt n}\]
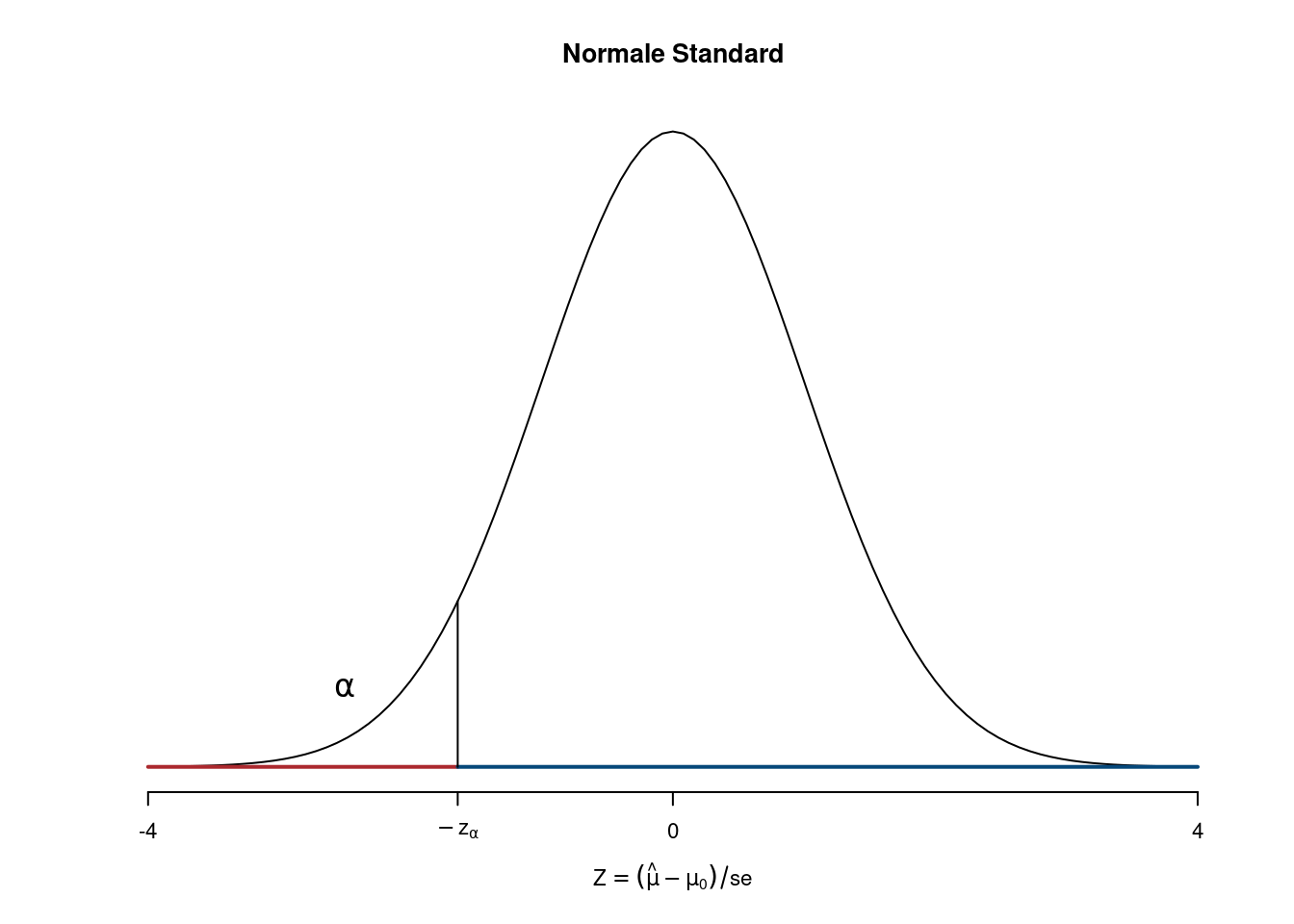
- Se \(z_{\text{obs}}>-z_\alpha\) \(H_0\) non viene rifiutata al livello di significatività \(\alpha\times100\%\)
- Se \(z_{\text{obs}}<-z_\alpha\) \(H_0\) viene rifiutata al livello di significatività \(\alpha\times100\%\)
Esempio 15.3 La durata, in ore, della resistenza di un transistor alle alte temperature sia \(X \,\sim\, N(\mu,\, \sigma^{2})\) e, in base all’esperienza, sia \(\mu_{0}=6\) ore e \(\sigma_{0}=0.5\) ore. Si apportano modifiche alla composizione dei materiali per fare diminuire la durata della resistenza alla temperatura. Si eseguono 16 osservazioni, dalle quali si ottiene una durata media \(\bar{x}=5.7\) e uno deviazione standard \(s=0.6\). Verificare l’ipotesi, al LdS dell’1%, che la resistenza sia rimasta invariata contro l’alternativa che sia diminuita.
Test \(Z\) per una media, variazna nota
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \mu = \mu_0=6h \\ H_1: \mu < \mu_0=6h \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)
\(\sigma^{2}\) di \(\cal{P}\) è nota: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {\sigma/\sqrt{n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 5.7 - 6 )} { 0.5 /\sqrt{ 16 }} = -2.4 \, . \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
La siginficatitività è \(\alpha=0.01\), dalle tavole osserviamo \(z_{0.01}=-2.3263\).
Essendo \(z_\text{obs}=-2.4<z_{0.01}=-2.3263\) allora rifiuto \(H_0\) al 1%.
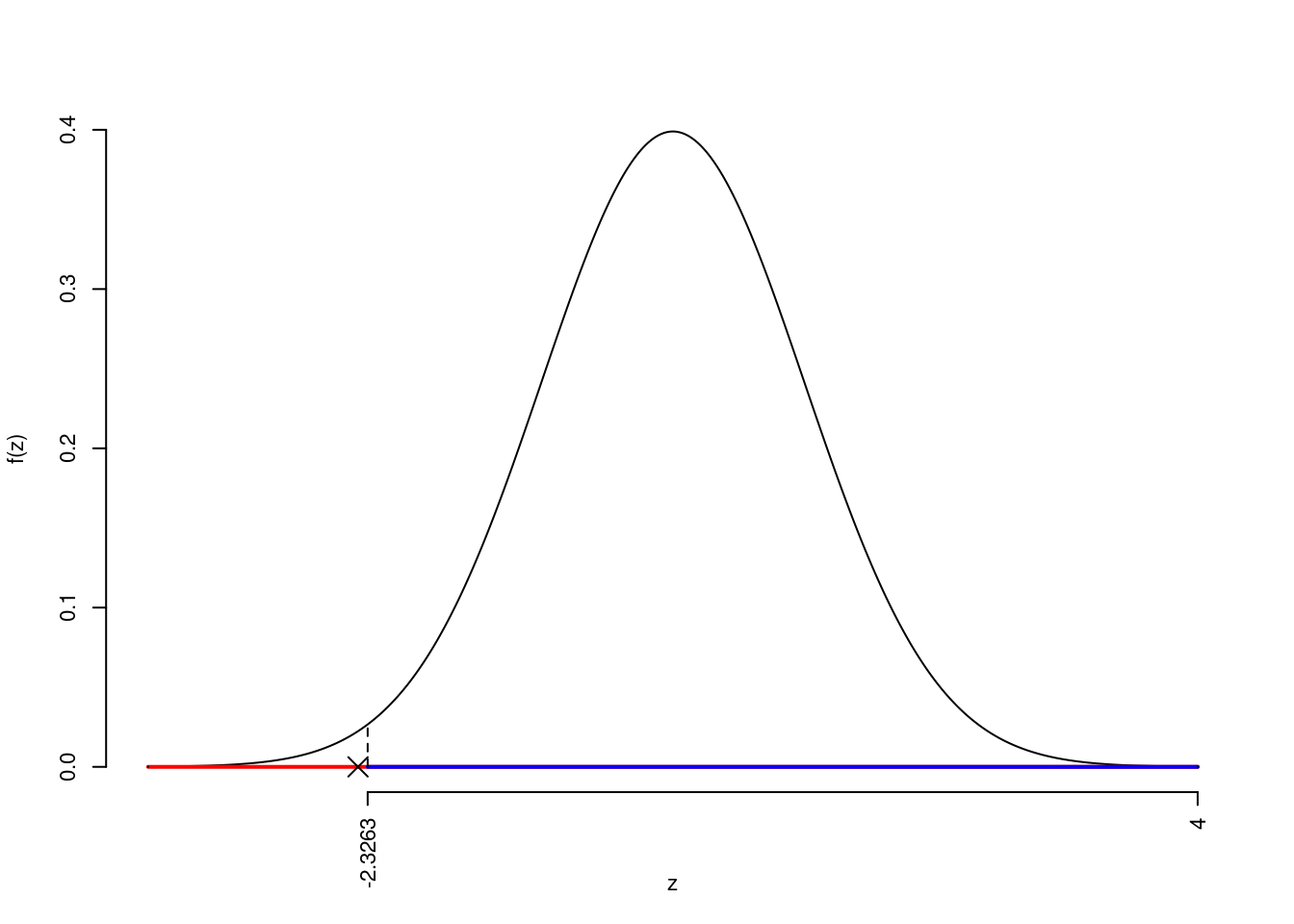
15.1.5.1 La probabilità di significatività osservata il \(p_\text{value}\)
Definizione 15.2 ($p_\text{value}$ caso unilaterale sinistro) Nel caso di ipotesi unilaterale sinistra abbiamo \[p_\text{value}=P(Z<z_{\text{obs}};H_0)\]
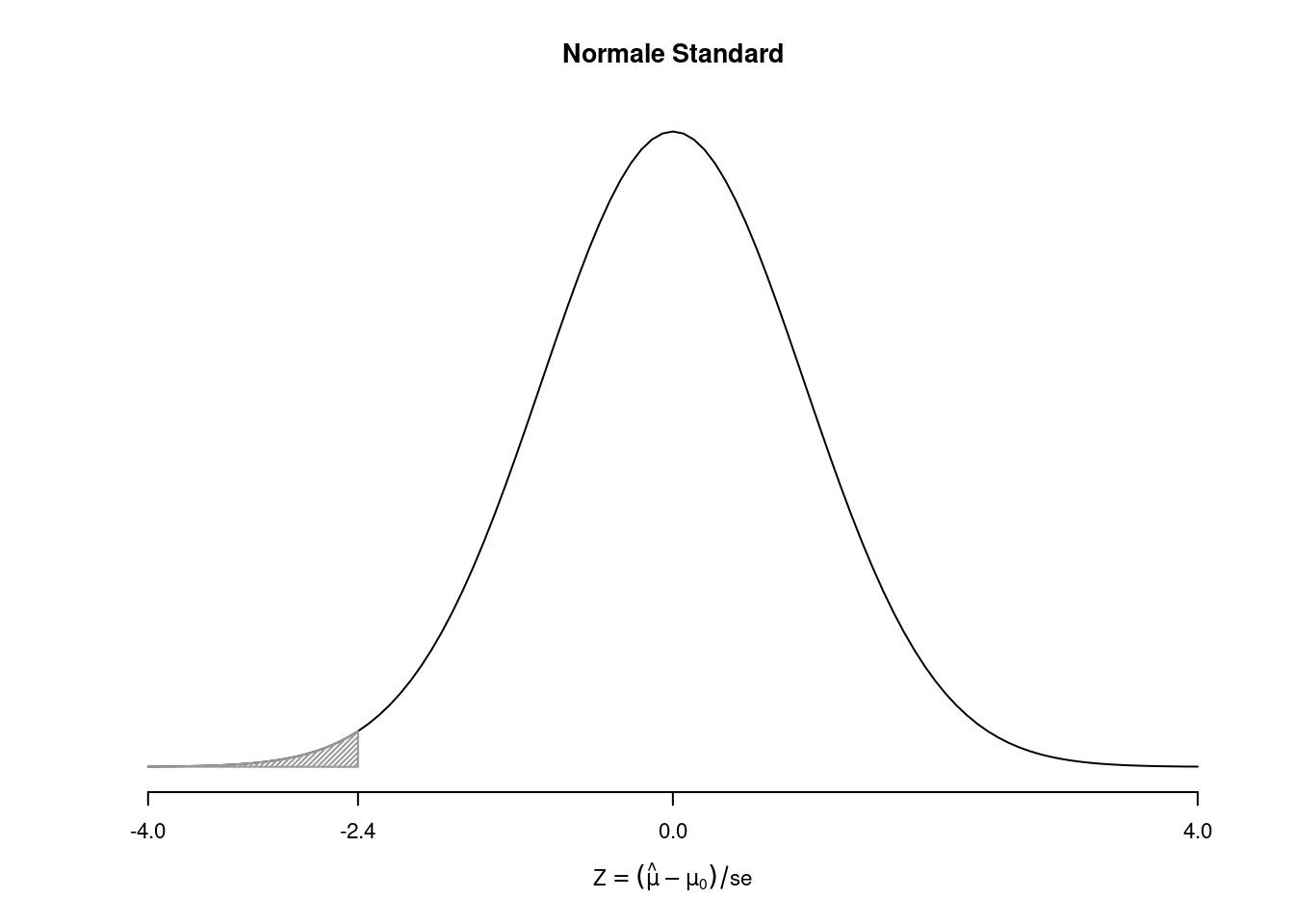
\[\begin{eqnarray*} p_{\text{value}}&=& P(Z<-2.4) \\ &=& \Phi(-2.4)\\ &=& 1-\Phi(2.4)\\ &=& 1-0.9918\\ &=& 0.0082 \end{eqnarray*}\]
15.1.6 Test sulla media, ipotesi bilaterale, \(\sigma^2\) noto
Siano \(X_1,...X_n\) \(n\) VC, IID: \(X_i\sim N(\mu,\sigma^2)\) con \(\sigma^2\) noto. Consideriamo il seguente sistema di ipotesi \[\begin{cases} H_0:\mu=\mu_0\\ H_1:\mu\neq\mu_0 \end{cases}\]
Sotto \(H_0\) la statistica \[Z=\frac{\hat\mu-\mu_0}{\sigma/\sqrt n}\sim N(0,1)\]
\(Z\) osservata sul campione misura l’evidenza contro \(H_0\), tanto più è il valore di \(Z\) è diverso da zero tanto più \(H_0\) è inverosimile
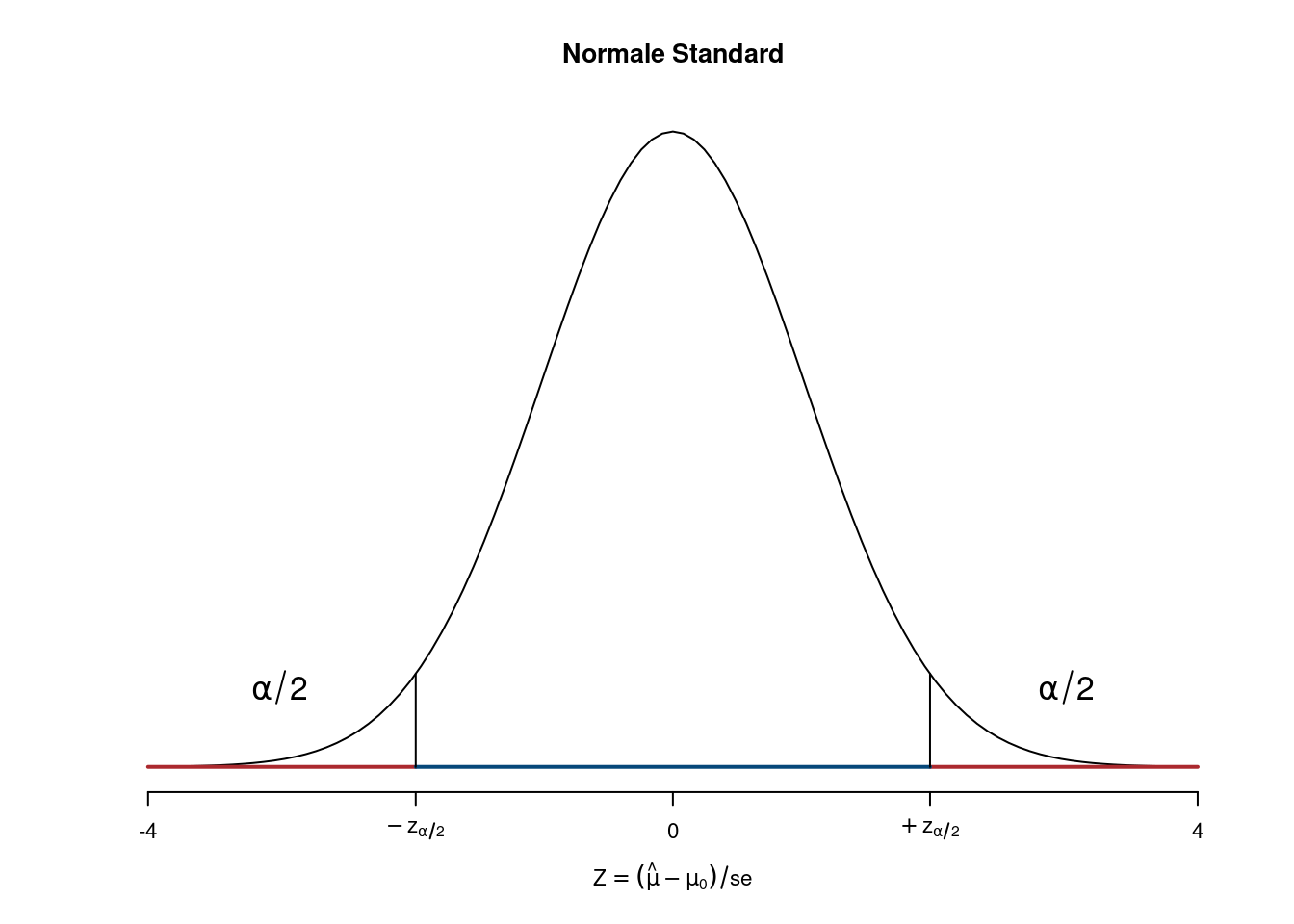
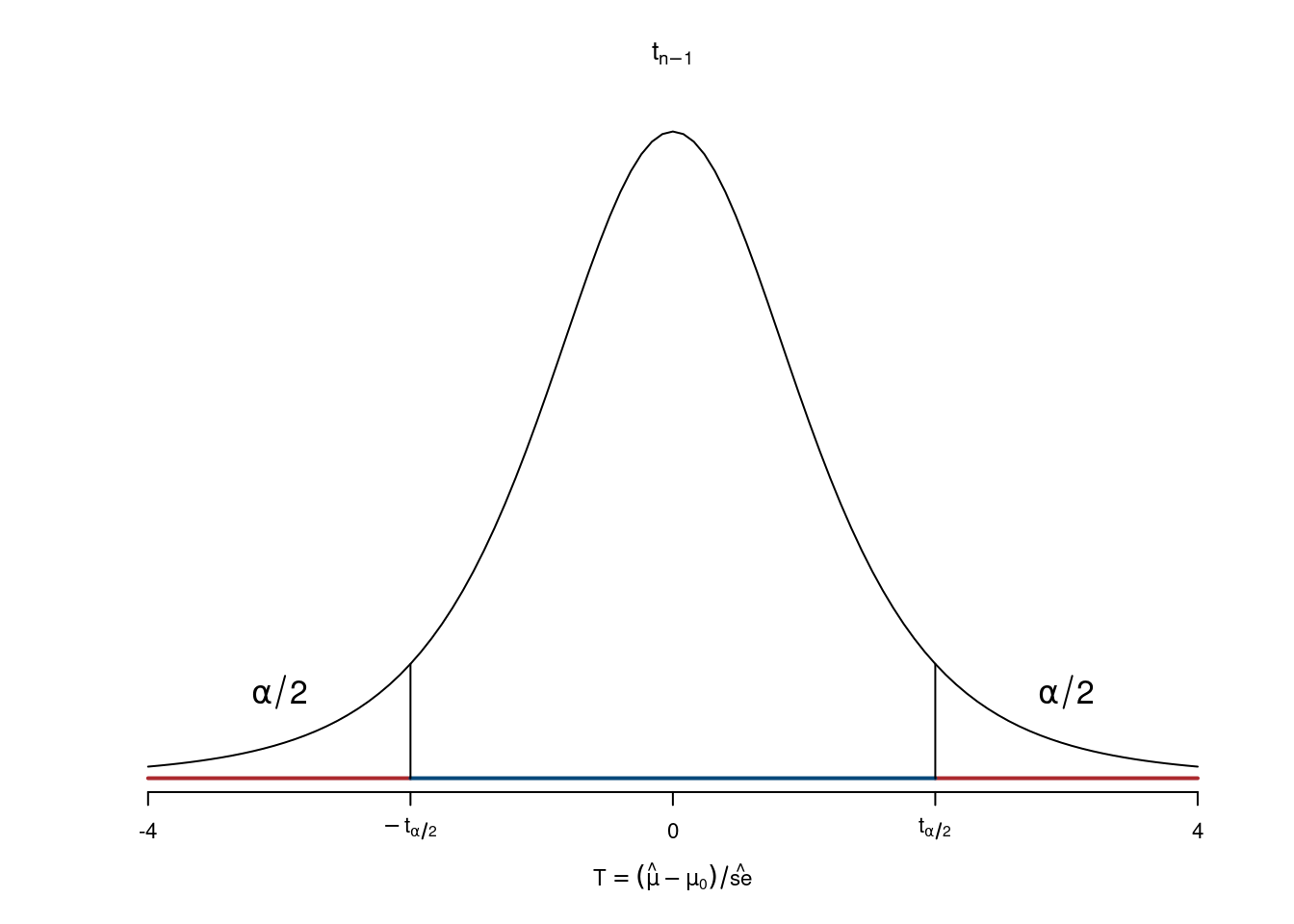
Decisione sul campione. Si decide un livello \(\alpha\) e si ricava \(z_{\alpha/2}\), si estrae un campione. Lo stimatore \(\hat\mu\) si realizza nella media osservata del campione \(\bar x\) \[z_{\text{obs}}=\frac{\bar x -\mu_0}{\sigma/\sqrt n}\]
- Se \(-z_{\alpha/2}\leq z_{\text{obs}}\leq z_{\alpha/2}\) \(H_0\) non viene rifiutata al livello di significatività \(\alpha\times100\%\)
- Se \(z_{\text{obs}}<-z_{\alpha/2}\), o \(z_{\text{obs}}>+z_{\alpha/2}\) \(H_0\) viene rifiutata al livello di significatività \(\alpha\times100\%\)
Esempio 15.4 Un produttore di semiconduttori afferma che la durata media dei suoi chip è di 300 ore con una deviazione standard di 3 ore. Un’azienda decide di testare la qualità dei chip e conduce un esperimento con 16 chip, ottenendo una durata media di 298 ore e una deviazione standard di 4 ore. I risultati di questo test sono coerenti con l’affermazione del produttore i chip tendono a durare in modo diverso dalla durata dichiarata, al 5%?
Test \(Z\) per una media, variazna nota
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \mu = \mu_0=300~h \\ H_1: \mu \neq \mu_0=300~h \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)
\(\sigma^{2}\) di \(\cal{P}\) è nota: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {\sigma/\sqrt{n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 298 - 300 )} { 3 /\sqrt{ 16 }} = -2.667 \, . \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
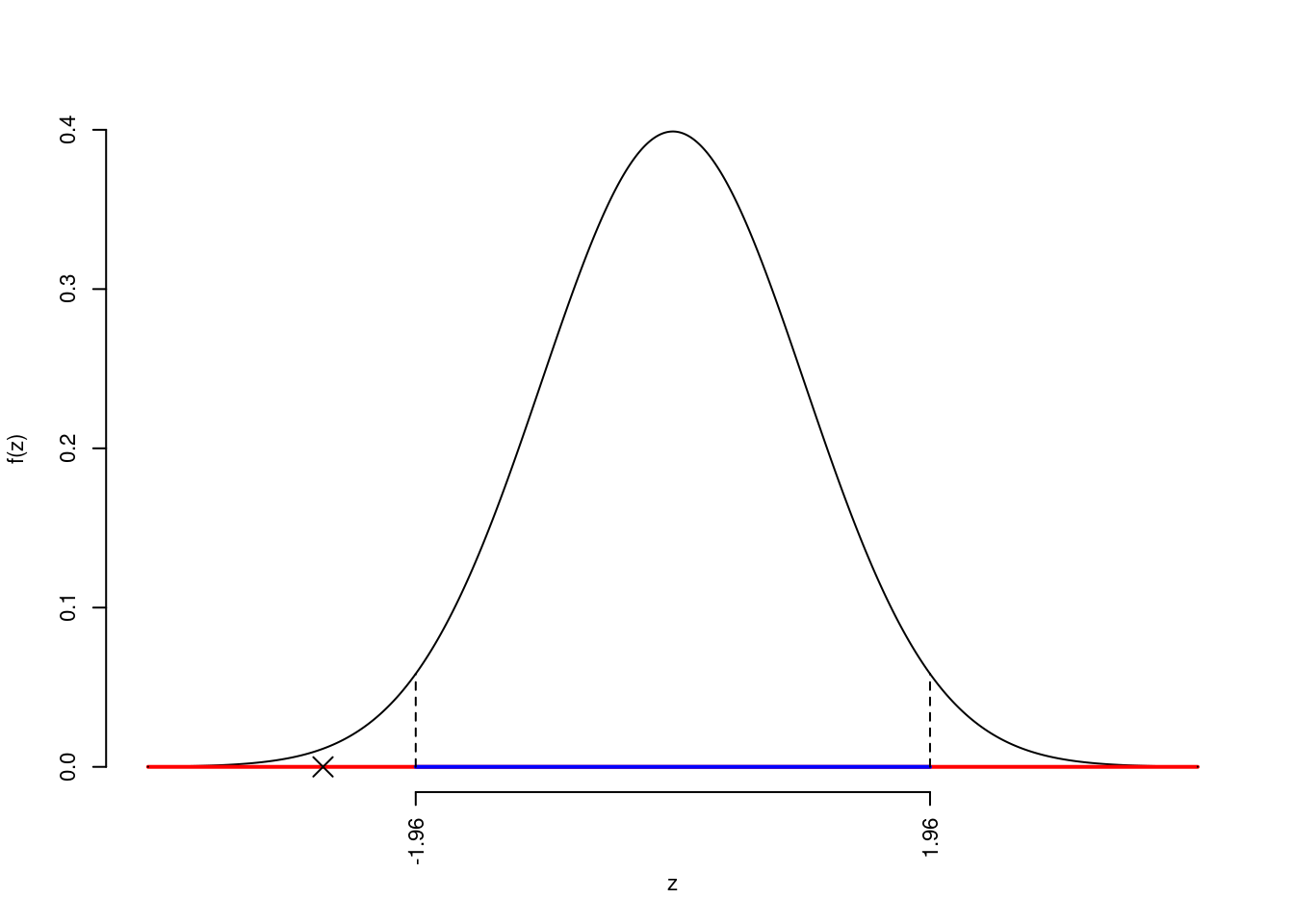
La siginficatitività è \(\alpha=0.05\), dalle tavole osserviamo \(z_{0.025}=1.96\).
Essendo \(|z_\text{obs}|=2.6667>z_{0.025}=1.96\) allora rifiuto \(H_0\) al 5%.
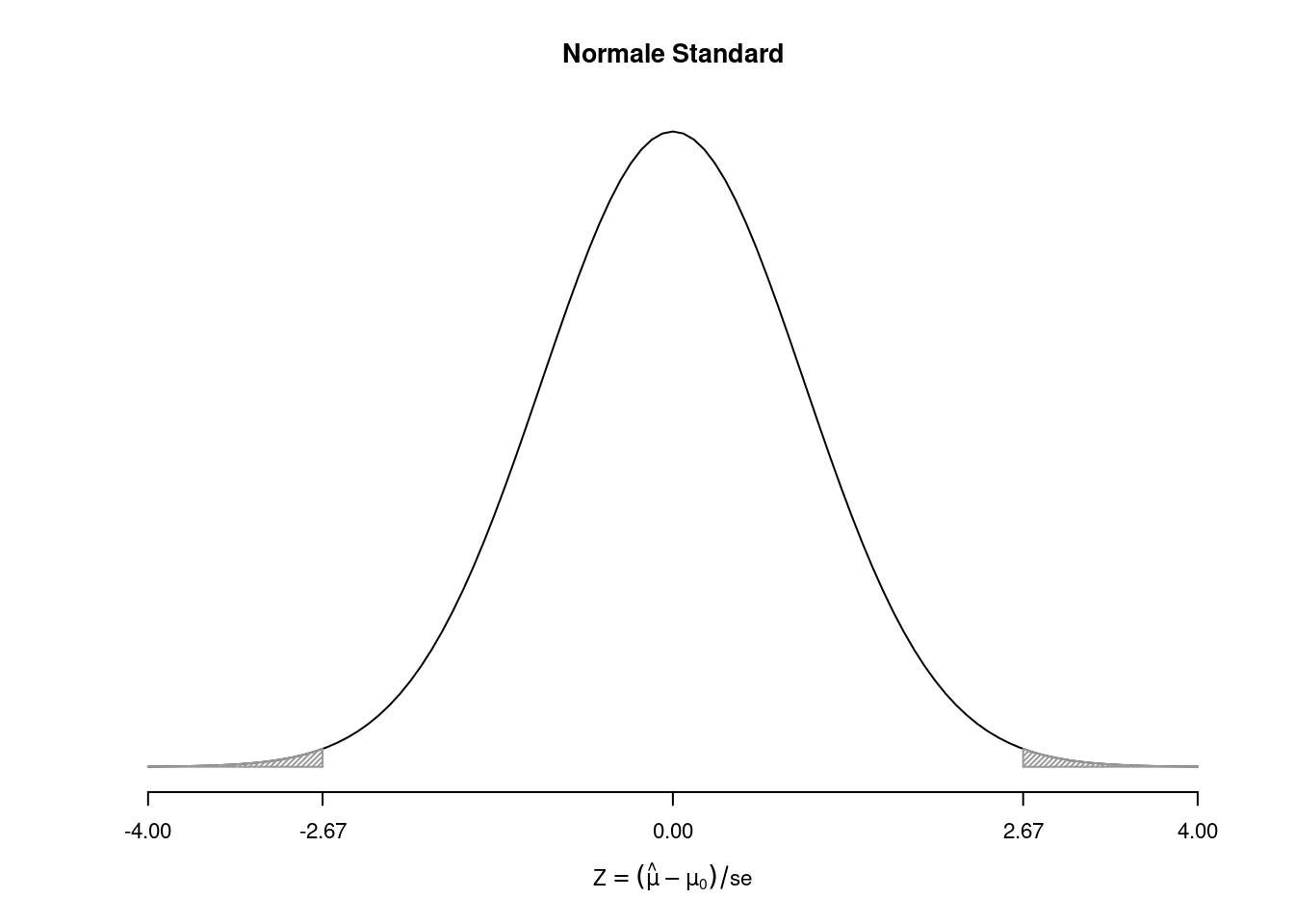
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(|Z|>|-2.67|)=2P(Z>2.67)=0.007661 \]
\[ 0.001 < p_\text{value}= 0.007661 \leq 0.01 \]
15.1.6.1 La probabilità di significatività osservata il \(p_\text{value}\)
Definizione 15.3 ($p_\text{value}$ caso bilaterale) Nel caso di ipotesi bilaterale abbiamo \[p_\text{value}=P(|Z|>|z_{\text{obs}}|;H_0)\]
15.2 Significatività non fissata
Le strategie per decidere per \(H_0\) invece di \(H_1\) cambiano a seconda di cosa rappresentano realmente le due ipotesi. In controllo di qualità industriale \(H_0\) significa conforme agli standard e \(H_1\) non conforme, fissare \(\alpha\) e di conseguenza \(\beta\) è frutto di un bilancio rischi benefici che richiede di esplicitare i costi che l’azienda paga in base all’errore: quando costa commettere l’errore di primo tipo? Quanto costa commettere l’errore di secondo tipo?
In altri contesti di ricerca la lontananza dei dati da \(H_0\) può essere oggetto di dibattito e il \(p_\text{value}\) misura esattamente questo. Senza avere fissato in anticipo \(\alpha\) il ricercatore di trova a discutere se il \(p_\text{value}\) è sufficientemente piccolo da rigettare l’ipotesi nulla. Il prossimo esempio esemplifica l’approccio
Esempio 15.5 Un’azienda farmaceutica afferma che la concentrazione media di principio attivo in una certa medicina è di 50 mg con una deviazione standard di 2 mg. Un laboratorio indipendente decide di verificare questa affermazione eseguendo 25 analisi e ottiene una concentrazione media di 51 mg e una deviazione standard di 2.5 mg. I risultati delle analisi sono coerenti con l’affermazione dell’azienda o la concentrazione del principio attivo è maggiore dalla quantità dichiarata?
Test \(Z\) per una media, variazna nota
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \mu = \mu_0=50mg \\ H_1: \mu > \mu_0=50mg \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\)
\(\sigma^{2}\) di \(\cal{P}\) è nota: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {\sigma/\sqrt{n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 51 - 50 )} { 2 /\sqrt{ 25 }} = 2.5 \, . \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
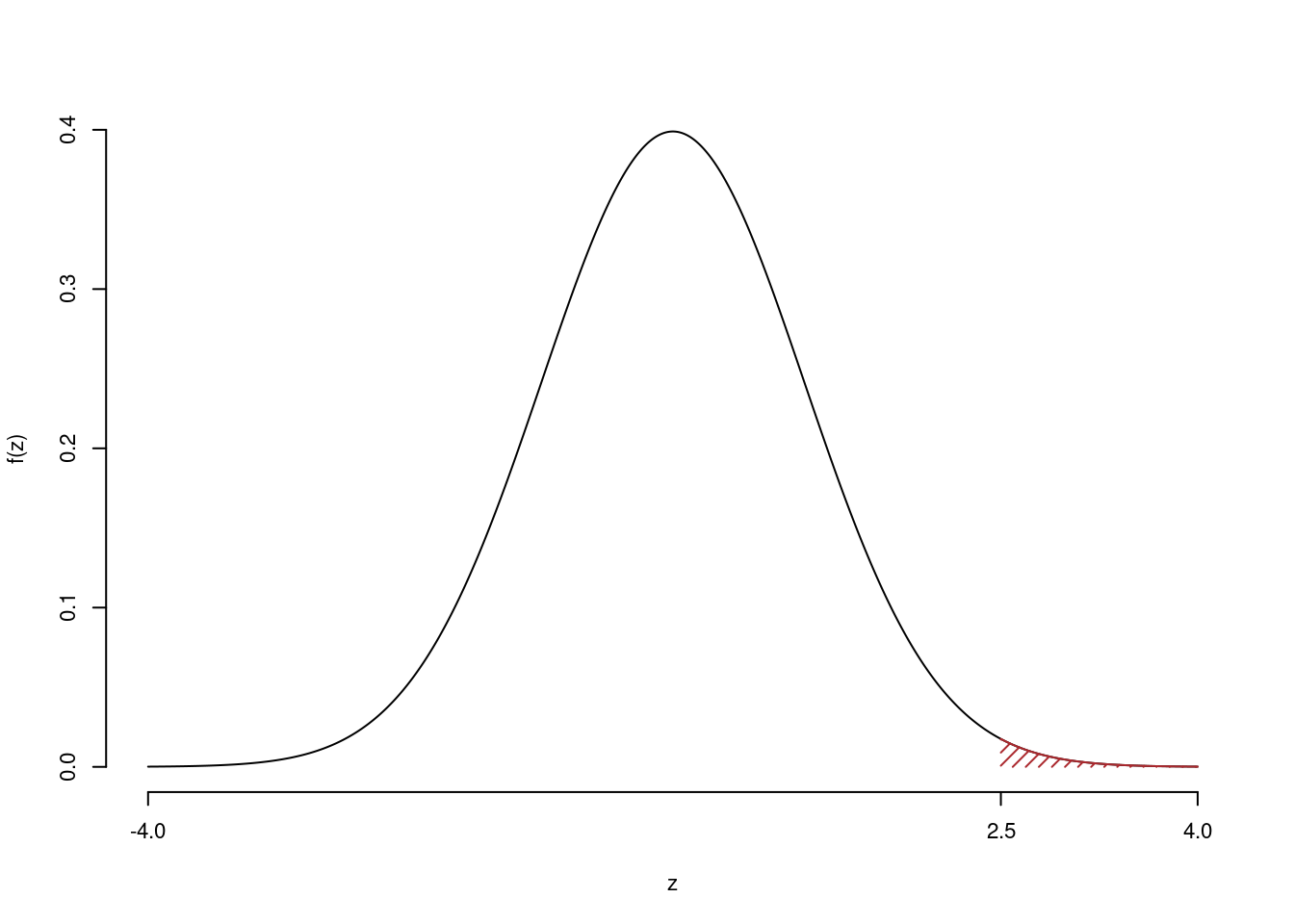
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(Z>2.5)=0.006210 \]
\[
0.001 < p_\text{value}= 0.006210 \leq 0.01
\]
Rifiuto \(H_0\) all’1%,
\(0.001<p_\text{value}<0.01\), molto significativo \(\fbox{**}\).
15.3 Test per \(\mu\), \(\sigma\) incognita
Se \(\sigma^2\) è incognito va stimato dai dati. Consideriamo lo stimatore \(S^2\) di \(\sigma^2\) \[S^2=\frac {1}{n-1}\sum_{i=1}^n (X_i-\hat \mu)^2=\frac {n}{n-1}\frac 1 n\sum_{i=1}^n (X_i-\hat \mu)^2=\frac n {n-1}\hat\sigma^2\]
Ricordiamo che \[\widehat{SE(\hat\mu)}=\sqrt{\frac {S^2}n}=\frac S {\sqrt n}\]
Ricordiamo infine che \[T=\frac{\hat \mu-\mu}{\widehat{SE(\hat\mu)}}\sim t_{n-1}\]
Ovvero \[T=\frac{\hat \mu-\mu}{S/\sqrt n}\sim t_{n-1}\]
E quindi sotto \(H_0\) \[T=\frac{\hat \mu-\mu_0}{S/\sqrt n}\sim t_{n-1}\] \(T\) è la statistica test che misura l’evidenza dei dati contro \(H_0\)
15.3.1 Test sulla media, ipotesi unilaterale destra, \(\sigma^2\) incognito
Siano \(X_1,...X_n\) \(n\) VC, IID: \(X_i\sim N(\mu,\sigma^2)\) con \(\sigma^2\) incognito.
Consideriamo il seguente sistema di ipotesi \[\begin{cases} H_0:\mu=\mu_0\\ H_1:\mu>\mu_0 \end{cases}\]
Sotto \(H_0\) la statistica \[T=\frac{\hat \mu-\mu_0}{S/\sqrt n}\sim t_{n-1}\]
La \(T\) osservata sul campione misura l’evidenza contro \(H_0\), tanto più è alto il valore di \(Z\) tanto più \(H_0\) è inverosimile
Decisione sul campione Si decide un livello \(\alpha\) e si ricava \(t_{n-1;\alpha}\), si estrae un campione. Lo stimatore \(\hat\mu\) si realizza nella media osservata del campione \(\bar x\) \[t_{\text{obs}}=\frac{\bar x -\mu_0}{S/\sqrt n}\]
- Se \(t_{\text{obs}}<t_{n-1;\alpha}\) \(H_0\) non viene rifiutata al livello di significatività \(\alpha\times100\%\)
- Se \(t_{\text{obs}}>t_{n-1;\alpha}\) \(H_0\) viene rifiutata al livello di significatività \(\alpha\times100\%\)
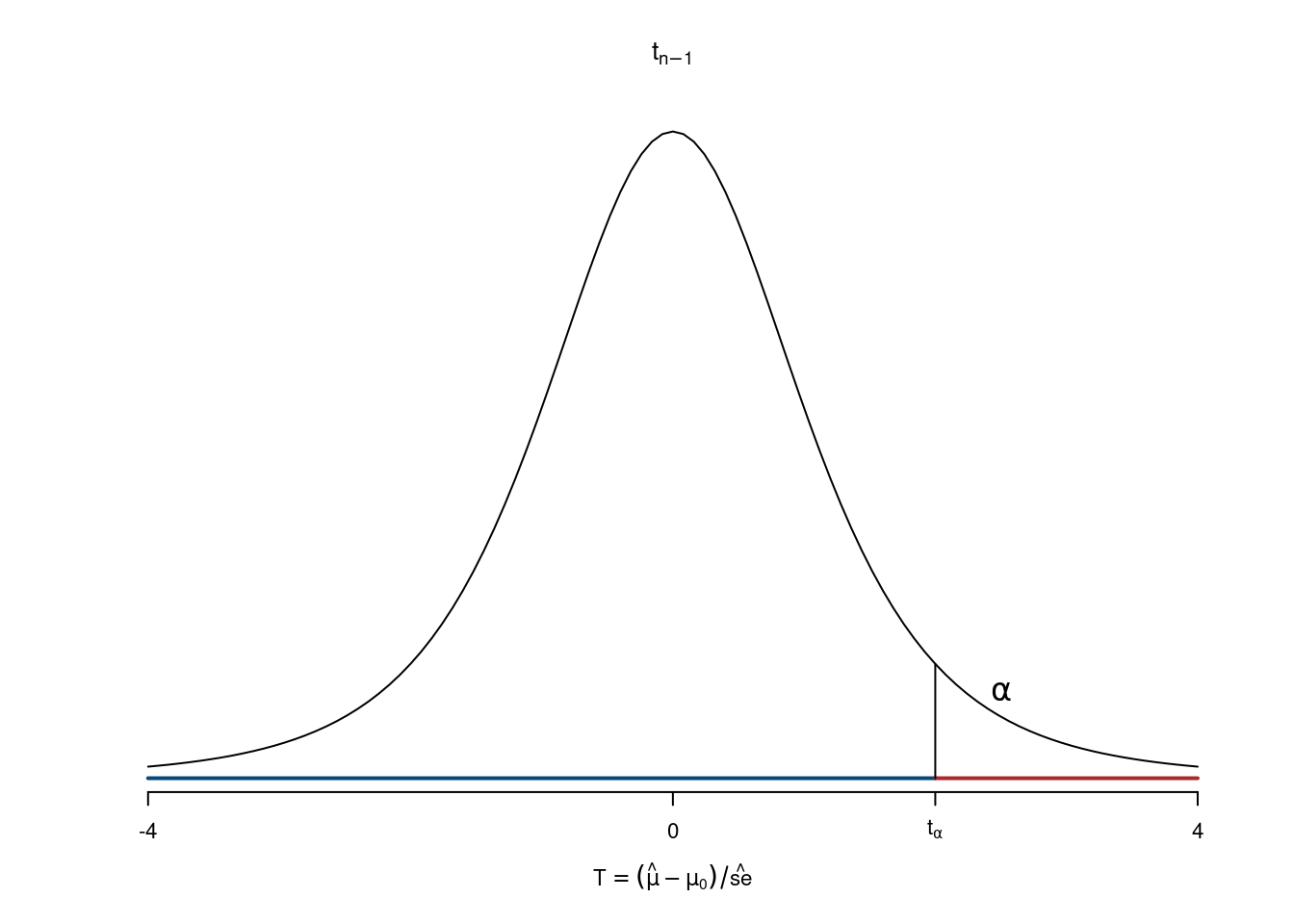
Esempio 15.6 Un produttore di aspirine afferma che il prodotto lenisce il mal di testa in 30 minuti. Un campione casuale di 25 persone la usa. Risultato: \(\bar{x}=31.4\)m con \(\hat{\sigma}= 4.2\)m. Verificare l’affermazione del produttore a un LdS del 5%.
Test \(t\) per una media, varianza incognita
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \mu = \mu_0=30m \\ H_1: \mu > \mu_0=30m \end{cases}\]
\[\begin{eqnarray*} S &=& \sqrt{\frac{n} {n-1}}\ \widehat{\sigma} = \sqrt{\frac{ 25 } { 25 -1}} \times 4.2 = 4.287 \end{eqnarray*}\] \[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {S/\,\sqrt{n}}&\sim&t_{n-1}\\ t_{\text{obs}} &=& \frac{ ( 31.4 - 30 )} { 4.287 /\sqrt{ 25 }} = 1.633 \, . \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
La siginficatitività è \(\alpha=0.05\), dalle tavole osserviamo \(t_{25-1;0.05}=1.7109\).
Essendo \(t_\text{obs}=1.633<t_{25-1;0.05}=1.7109\) allora non rifiuto \(H_0\) al 5%.
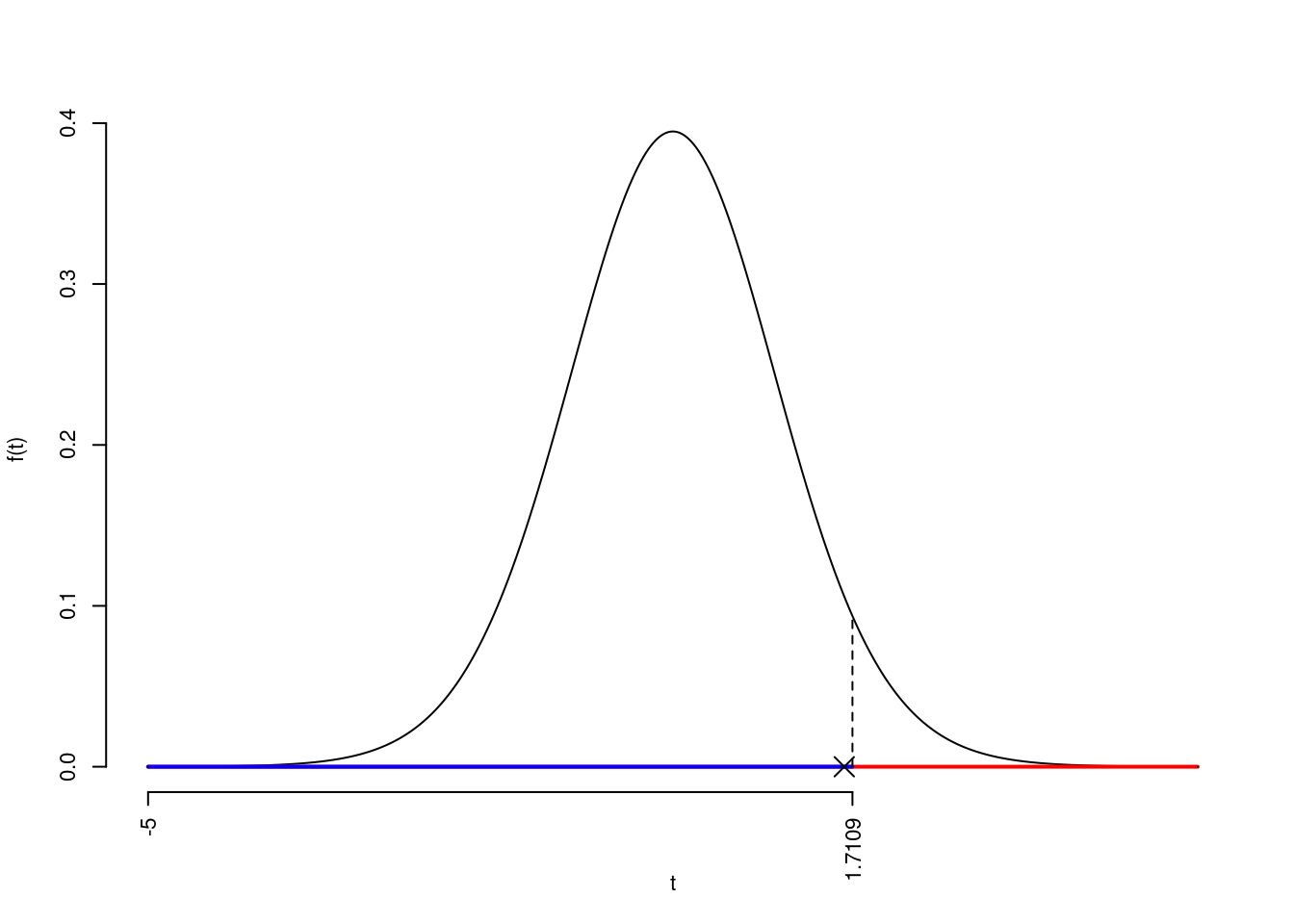
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(T_{25-1}>1.63)=0.057761 \]
Attenzione il calcolo del \(p_\text{value}\) con la \(T\) è puramente illustrativo e non può essere riprodotto senza una calcolatrice statistica adeguata.\[ 0.05 < p_\text{value}= 0.057761 \leq 0.1 \]
15.3.2 Test sulla media, ipotesi unilaterale sinistra, \(\sigma^2\) incognito
Siano \(X_1,...X_n\) \(n\) VC, IID: \(X_i\sim N(\mu,\sigma^2)\) con \(\sigma^2\) incognito. Consideriamo il seguente sistema di ipotesi \[\begin{cases} H_0:\mu=\mu_0\\ H_1:\mu<\mu_0 \end{cases}\]
Sotto \(H_0\) la statistica \[T=\frac{\hat \mu-\mu_0}{S/\sqrt n}\sim t_{n-1}\]
Lo stimatore \(\hat\mu\) si realizza nella media osservata del campione \(\bar x\) \[t_{\text{obs}}=\frac{\bar x -\mu_0}{S/\sqrt n}\]
Decisione sul campione Si decide un livello \(\alpha\) e si ricava \(t_{n-1;\alpha}\), si estrae un campione. Lo stimatore \(\hat\mu\) si realizza nella media osservata del campione \(\bar x\) \[t_{\text{obs}}=\frac{\bar x -\mu_0}{S/\sqrt n}\]
- Se \(t_{\text{obs}}>-t_{n-1;\alpha}\) \(H_0\) non viene rifiutata al livello di significatività \(\alpha\times100\%\)
- Se \(t_{\text{obs}}<-t_{n-1;\alpha}\) \(H_0\) viene rifiutata al livello di significatività \(\alpha\times100\%\)
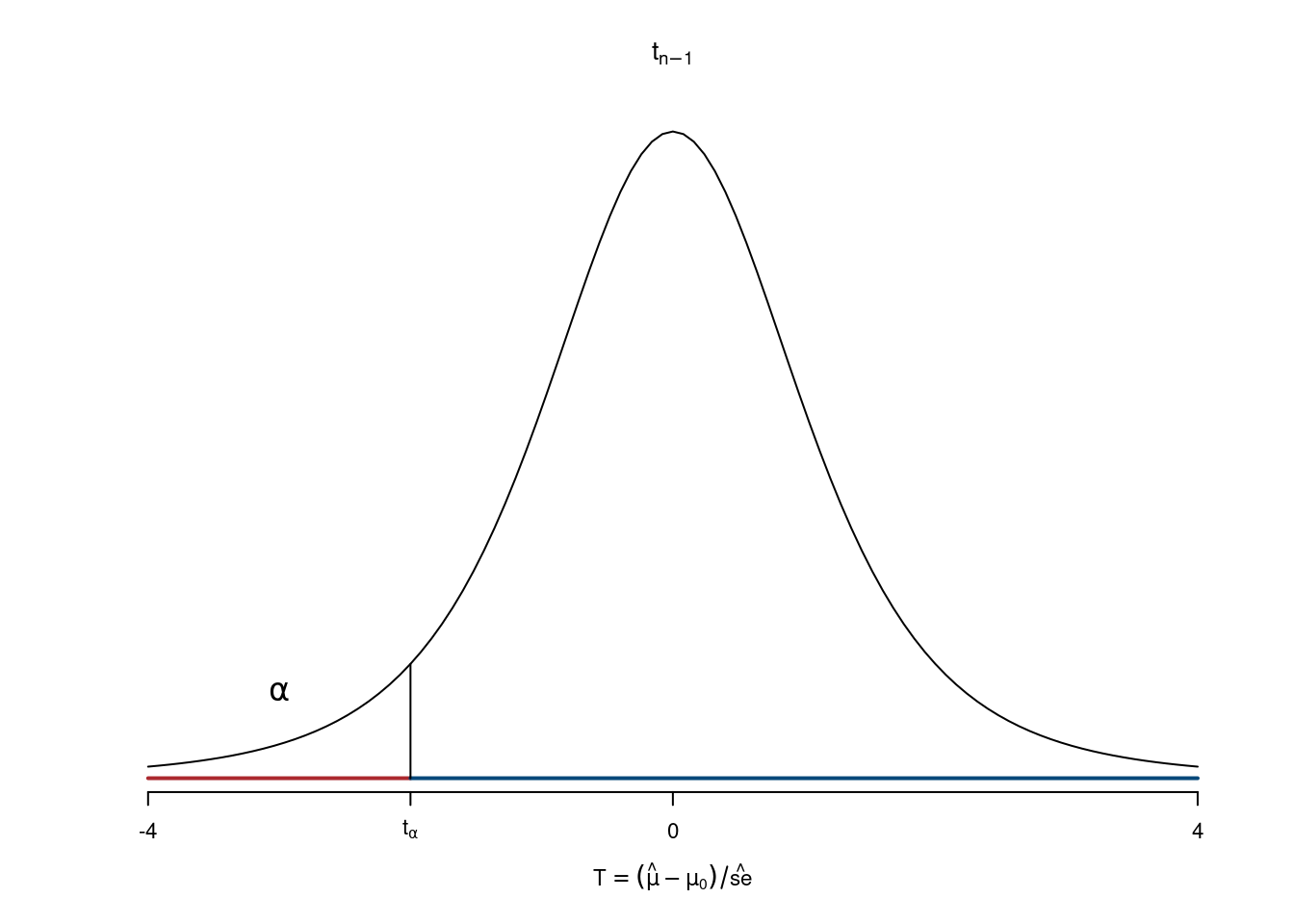
Esempio 15.7 Un Centro dietetico afferma che con i loro programmi si perdono in media 2kg nella prima settimana. Si selezionano casualmente 25 soggetti, tra gli iscritti al programma.
Risultato: \(\overline{\Delta x}=1.5\)kg con \(\hat\sigma=1.4\)kg. Verificare l’affermazione del Centro al LdS del 5%.
Test \(t\) per una media, varianza incognita
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \mu = \mu_0=2kg \\ H_1: \mu < \mu_0=2kg \end{cases}\]
\[\begin{eqnarray*} S &=& \sqrt{\frac{n} {n-1}}\ \widehat{\sigma} = \sqrt{\frac{ 25 } { 25 -1}} \times 1.4 = 1.429 \end{eqnarray*}\] \[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {S/\,\sqrt{n}}&\sim&t_{n-1}\\ t_{\text{obs}} &=& \frac{ ( 1.5 - 2 )} { 1.429 /\sqrt{ 25 }} = -1.75 \, . \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
La siginficatitività è \(\alpha=0.05\), dalle tavole osserviamo \(t_{25-1;0.05}=-1.7109\).
Essendo \(t_\text{obs}=-1.7496<t_{25-1;0.05}=-1.7109\) allora rifiuto \(H_0\) al 5%.
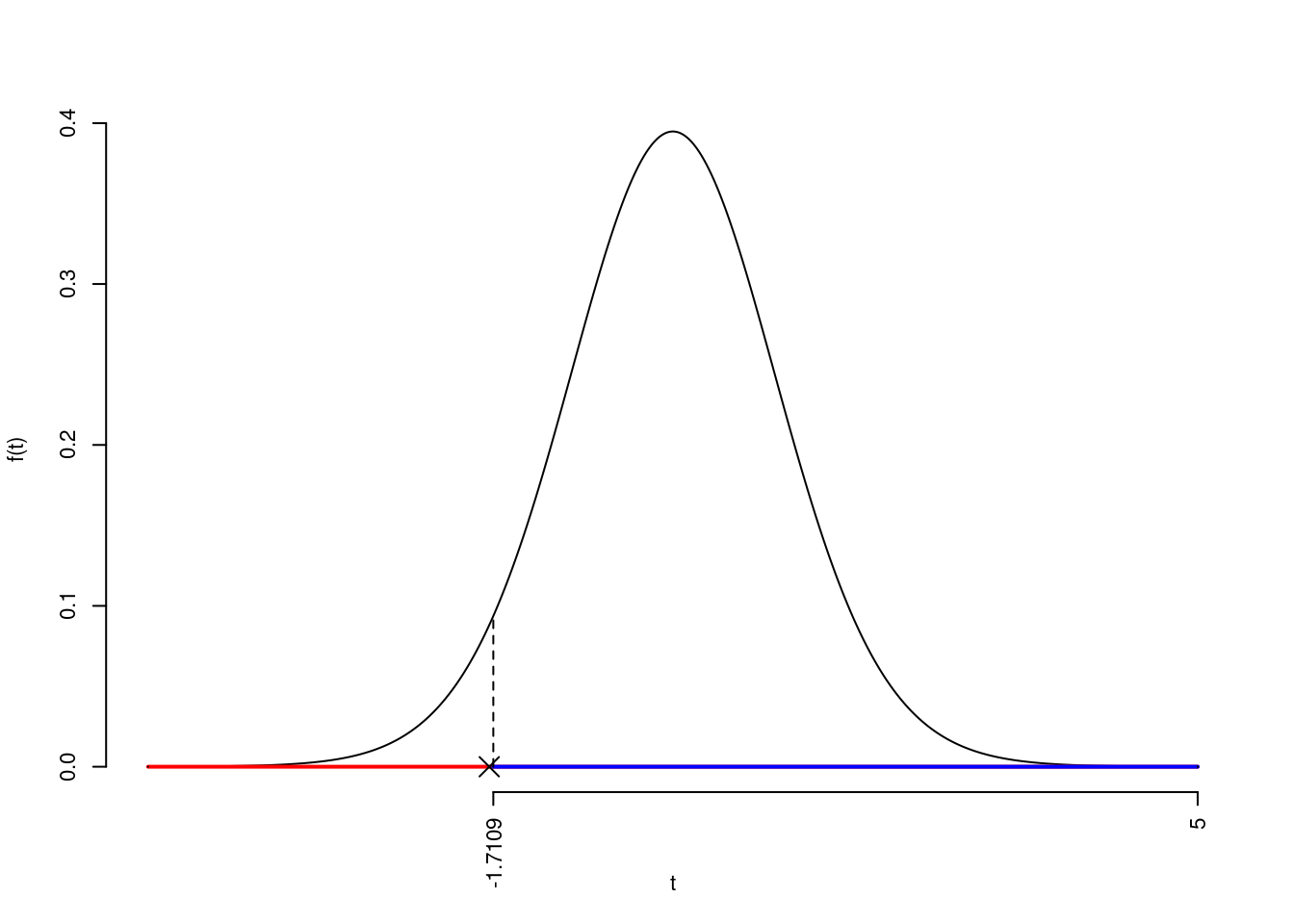
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(T_{25-1}<-1.75)=0.046480 \]
Attenzione il calcolo del \(p_\text{value}\) con la \(T\) è puramente illustrativo e non può essere riprodotto senza una calcolatrice statistica adeguata.\[ 0.01 < p_\text{value}= 0.046480 \leq 0.05 \]
15.3.3 Test sulla media, ipotesi bilaterale, \(\sigma^2\) incognito
Siano \(X_1,...X_n\) \(n\) VC, IID: \(X_i\sim N(\mu,\sigma^2)\) con \(\sigma^2\) incognito. Consideriamo il seguente sistema di ipotesi \[\begin{cases} H_0:\mu=\mu_0\\ H_1:\mu\neq\mu_0 \end{cases}\]
Sotto \(H_0\) la statistica \[T=\frac{\hat \mu-\mu_0}{S/\sqrt n}\sim t_{n-1}\]
Decisione sul campione. Si decide un livello \(\alpha\) e si ricava \(t_{n-1;\alpha}\), si estrae un campione. Lo stimatore \(\hat\mu\) si realizza nella media osservata del campione \(\bar x\) \[t_{\text{obs}}=\frac{\bar x -\mu_0}{S/\sqrt n}\]
- Se \(-t_{n-1;\alpha/2}<t_{\text{obs}}<t_{n-1;\alpha/2}\) \(H_0\) non viene rifiutata al livello di significatività \(\alpha\times100\%\)
- Se \(t_{\text{obs}}>t_{n-1;\alpha/2}\) o \(t_{\text{obs}}<-t_{n-1;\alpha/2}\) \(H_0\) viene rifiutata al livello di significatività \(\alpha\times100\%\)
Esempio 15.8 Eseguite 17 misure di resistenza su 17 campioni di filo. Risultato: la media è 7.5N (Newton) con \(\hat\sigma=\) 1.2N.
Il filo è stato ottenuto con un nuovo procedimento, ma non si conoscono i possibili effetti sulla resistenza. Verificare, a un LdS del 5%, l’ipotesi che la resistenza media sia uguale al filo standard, che è 6.8N, contro l’alternativa che sia diverso.
Test \(t\) per una media, varianza incognita
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \mu = \mu_0=6.8N \\ H_1: \mu \neq \mu_0=6.8N \end{cases}\]
\[\begin{eqnarray*} S &=& \sqrt{\frac{n} {n-1}}\ \widehat{\sigma} = \sqrt{\frac{ 17 } { 17 -1}} \times 1.2 = 1.237 \end{eqnarray*}\] \[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {S/\,\sqrt{n}}&\sim&t_{n-1}\\ t_{\text{obs}} &=& \frac{ ( 7.5 - 6.8 )} { 1.237 /\sqrt{ 17 }} = 2.333 \, . \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
La siginficatitività è \(\alpha=0.05\), dalle tavole osserviamo \(t_{17-1;0.025}=2.1199\).
Essendo \(|t_\text{obs}|=2.3333>t_{17-1;0.025}=2.1199\) allora rifiuto \(H_0\) al 5%.
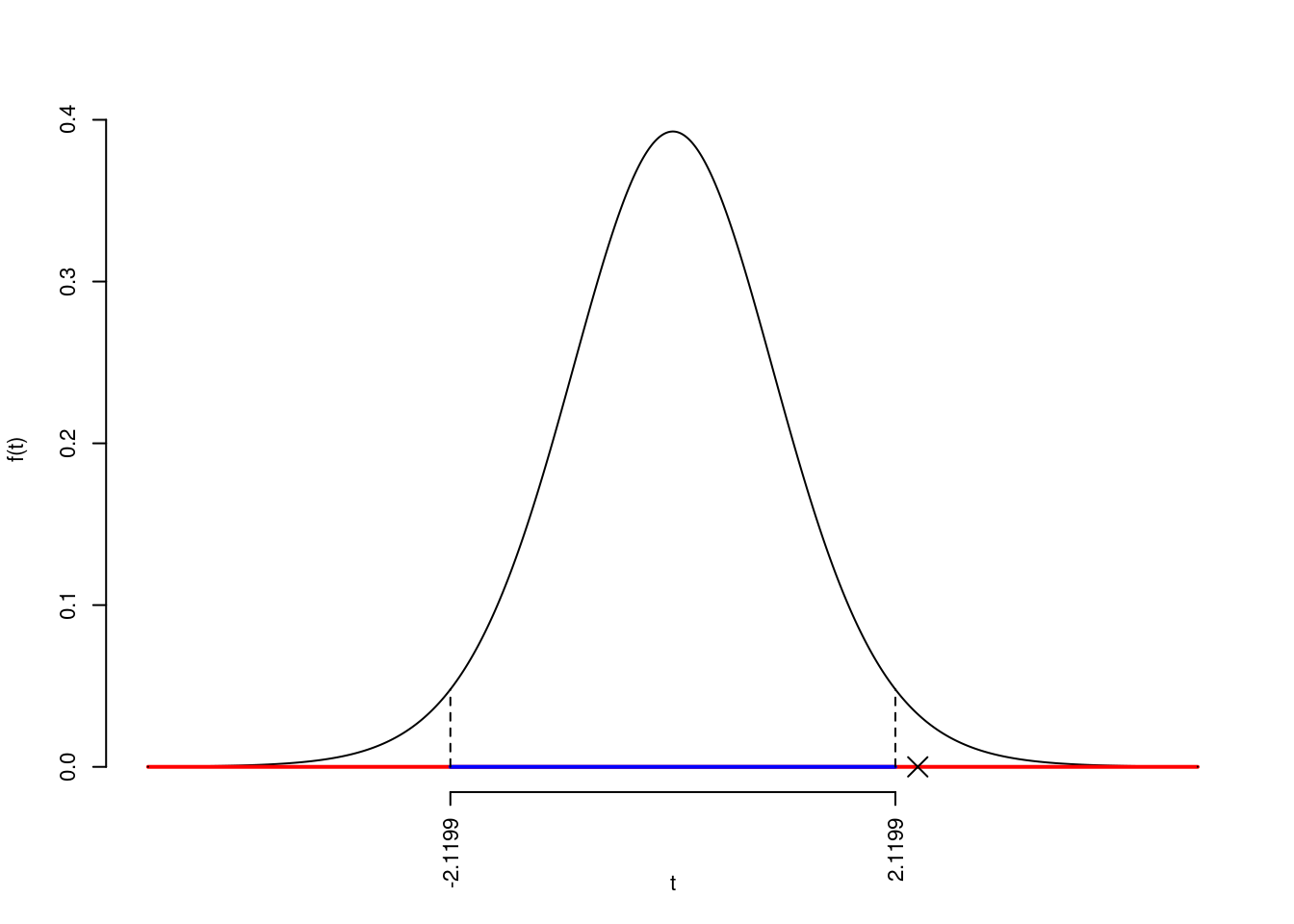
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(|T_{17-1}|>|2.33|)=2P(T_{17-1}>2.33)=0.033005 \]
Attenzione il calcolo del \(p_\text{value}\) con la \(T\) è puramente illustrativo e non può essere riprodotto senza una calcolatrice statistica adeguata.\[ 0.01 < p_\text{value}= 0.033005 \leq 0.05 \]
15.3.4 Significatività non fissata
Come per lo \(z\)-test se la significatività non è fissata potremmo interpretare il solo \(p_\text{value}\), ma il \(p_\text{value}\) per la distribuzione \(t\) non è calcolabile senza un’opportuna funzione che manca nelle gran parte delle calcolatrici scientifiche.
Se non si dispone di un software adeguato si possono usare le tavole statistiche e ricavare le soglie critiche per diversi \(\alpha\). Una strategia comune è fissare
\[ \alpha=\{1/10,1/20,1/100,1/1000\}=\{0.1,0.05,0.01,0.001\}, \]
ricavare dalle tavole i rispettivi \(t_{n-1,\alpha}\) (\(t_{n-1,\alpha/2}\), se il test è bilaterale) e vedere dove cade il \(t_\text{obs}\)
Esempio 15.9 Un’azienda farmaceutica afferma che la concentrazione media di principio attivo in una certa medicina è di 50 mg. Un laboratorio indipendente decide di verificare questa affermazione eseguendo 25 analisi e ottiene una concentrazione media di 51 mg e una deviazione standard di 2.5 mg. I risultati delle analisi sono coerenti con l’affermazione dell’azienda o la concentrazione del principio attivo tende a differire dalla quantità dichiarata?
Test \(t\) per una media, varianza incognita
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \mu = \mu_0=50\% \\ H_1: \mu \neq \mu_0=50\% \end{cases}\]
\[\begin{eqnarray*} S &=& \sqrt{\frac{n} {n-1}}\ \widehat{\sigma} = \sqrt{\frac{ 25 } { 25 -1}} \times 2.5 = 2.552 \end{eqnarray*}\] \[\begin{eqnarray*} \frac{\hat\mu - \mu_{0}} {S/\,\sqrt{n}}&\sim&t_{n-1}\\ t_{\text{obs}} &=& \frac{ ( 51 - 50 )} { 2.552 /\sqrt{ 25 }} = 1.96 \, . \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
Siccome \(H_1\) è bilaterale, considereremo \(\alpha/2\), anziché \(\alpha\)
\(\alpha=0.1, 0.05, 0.01, 0.001\) e quindi \(\alpha/2=0.05, 0.025, 0.005, 0.0005\)
I valori critici sono
\(t_{25-1;0.05}=1.7109\); \(t_{25-1;0.025}=2.0639\); \(t_{25-1;0.005}=2.7969\); \(t_{25-1;0.0005}=3.7454\)
Siccome \(1.7109<|t_\text{obs}|=1.9596<2.0639\), indecisione sul rifiuto di \(H_0\) al 10%,
\(0.05<p_\text{value}<0.1\), marginalmente significativo \(\fbox{.}\).
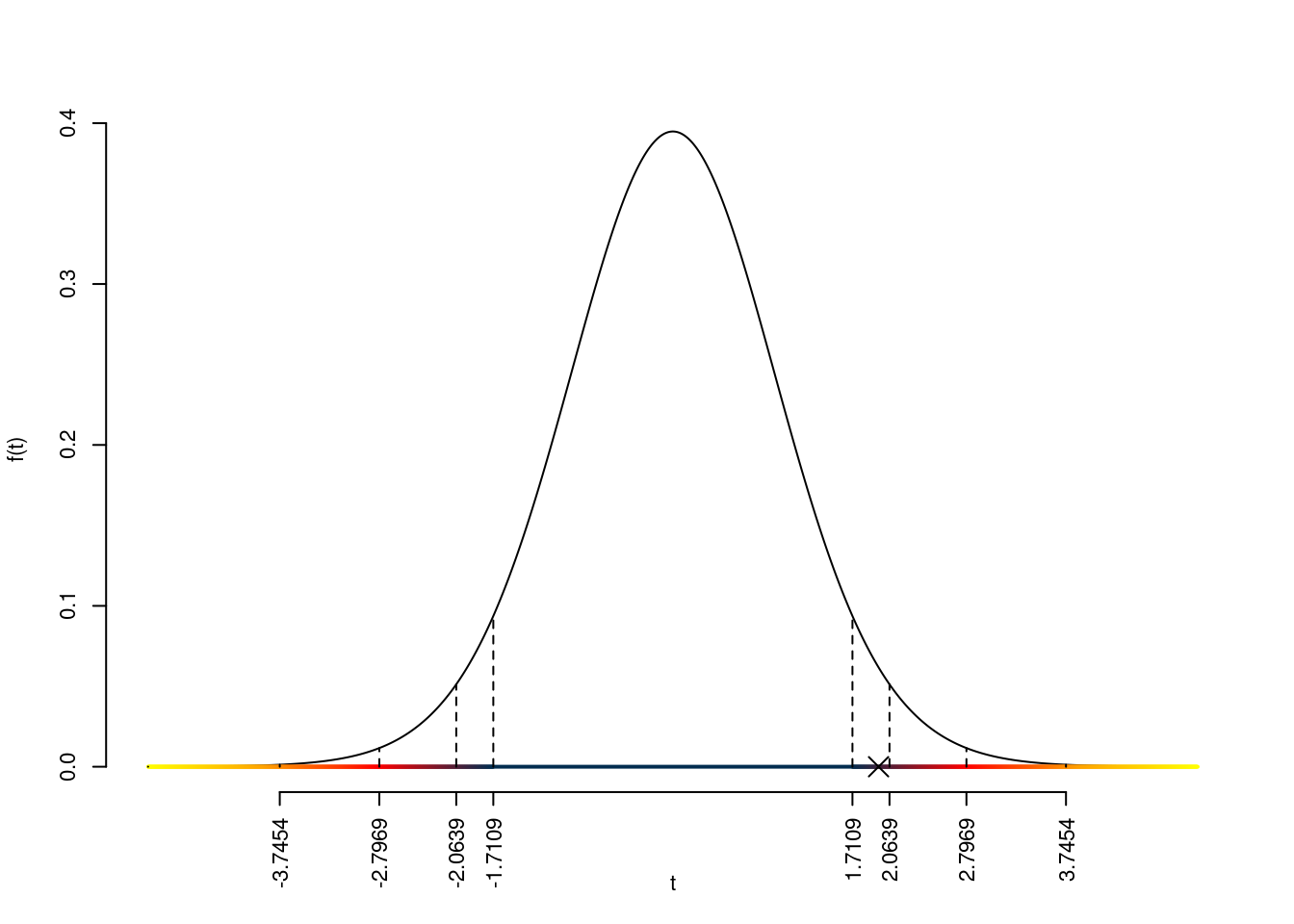
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(|T_{25-1}|>|1.96|)=2P(T_{25-1}>1.96)=0.061756 \]
Attenzione il calcolo del \(p_\text{value}\) con la \(T\) è puramente illustrativo e non può essere riprodotto senza una calcolatrice statistica adeguata.\[ 0.05 < p_\text{value}= 0.061756 \leq 0.1 \]
15.4 Massima verosimiglianza e test
Se \(\hat\theta\) è stimatore di massima verosimiglianza per \(\theta\) allora, per \(n\) sufficientemente grande \[\hat\theta\sim N(\theta, SE^2(\hat\theta))\]
Sotto ipotesi \(H_0\) \[\hat\theta\sim N(\theta_0, SE^2(\hat\theta))\]
La statistica test \[Z=\frac{\hat\theta-\theta_0}{SE(\hat\theta)}\sim N(0,1)\]
Esempio: se \(\sigma\) è incognita, la statistica test per \(\mu\) è: \[T=\frac{\hat\mu-\mu_0}{S/\sqrt n}\sim t_{n-1}\]
Se \(n\) diverge \[t_{n-1}\to N(0,1)\]
Se \(n>100\) il \(t\)-test diventa lo \(z\)-test.
15.5 Test per \(\pi\)
Siano \(X_1,...,X_n\) \(n\) VC IID, replicazioni di \(X\sim\text{Ber}(\pi)\). Lo stimatore di massima verosimiglianza \[\hat\pi=\frac 1 n \sum_{i=1}^n X_i\operatorname*{\sim}_a N\left(\pi,\frac{\pi(1-\pi)}{n}\right)\]
Sotto \(H_0\), \(\pi=\pi_0\) \[\hat\pi\operatorname*{\sim}_a N\left(\pi_0,\frac{\pi_0(1-\pi_0)}{n}\right)\]
E quindi \[\frac{\hat\pi-\pi_0}{\sqrt{\pi_0(1-\pi_0)/n}}\operatorname*{\sim}_a N(0,1)\]
La statistica osservata è \[z_{\text{obs}}=\frac{\hat\pi_{\text{obs}}-\pi_0}{\sqrt{\pi_0(1-\pi_0)/n}}\]
A seconda di \(H_1\) decideremo con le solite regole
Esempio 15.10 Lanciamo \(n=50\) un moneta di cui non siamo sicuri se è truccata oppure no. Osserviamo 30 successi su 50 lanci. Verificare l’ipotesi che la moneta sia bilanciata (\(\pi=0.5\)), contro l’alternativa che sia maggiore.
Lo stimatore di massima verosimiglianza è \[\hat\pi=\frac 1 n \sum_{i=1}^n X_i\]
Test \(Z\) per una proporzione
La stima \[\hat\pi=\frac { 30 } { 50 }= 0.6 \]
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \pi = \pi_0=0.5 \\ H_1: \pi > \pi_0=0.5 \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\) Test Binomiale per \(n\) grande: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\pi - \pi_{0}} {\sqrt {\pi_0(1-\pi_0)/\,n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 0.6 - 0.5 )} {\sqrt{ 0.5 (1- 0.5 )/ 50 }} = 1.414 \,. \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
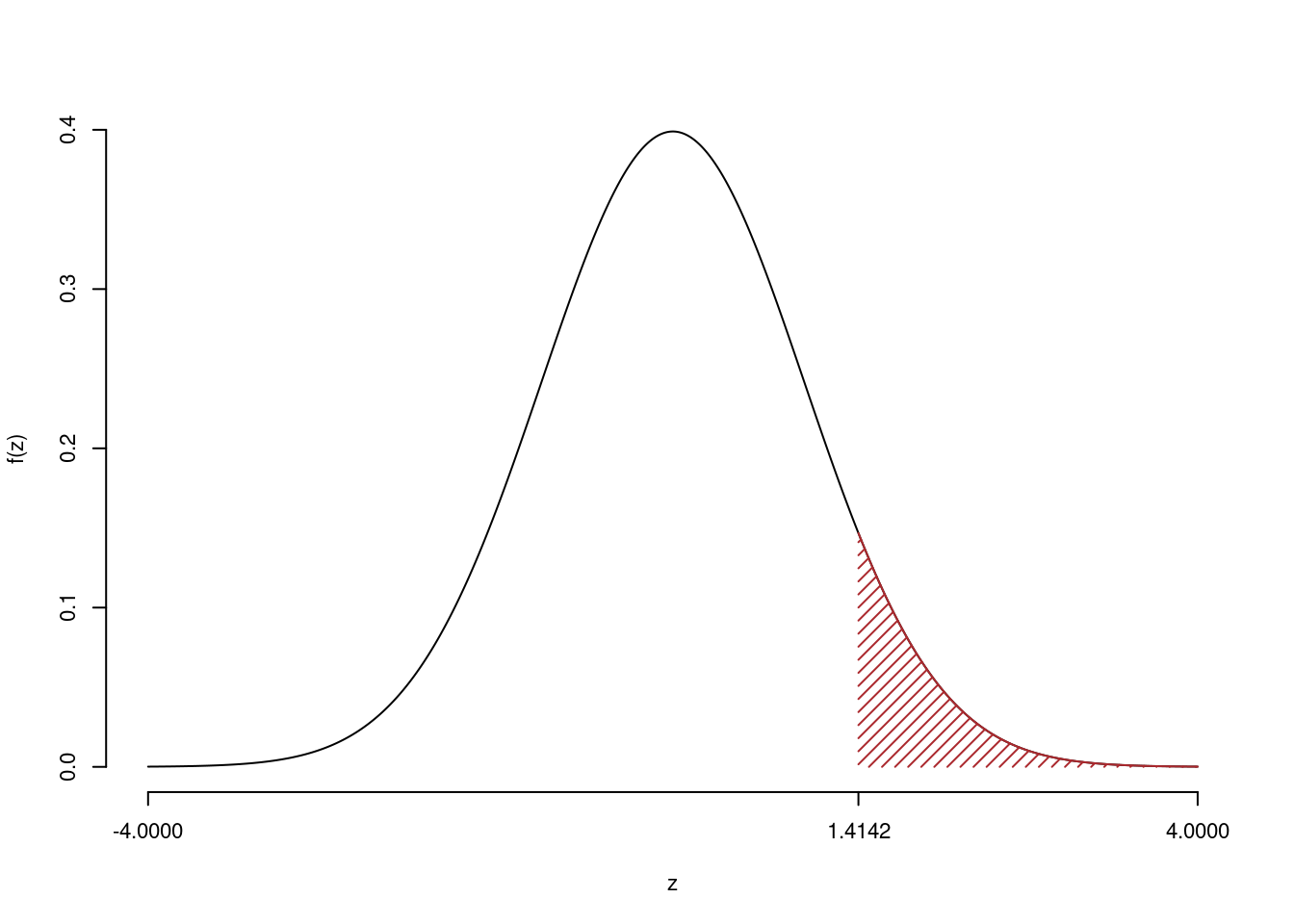
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(Z>1.41)=0.078650 \]
\[
0.05 < p_\text{value}= 0.078650 \leq 0.1
\]
Indecisione sul rifiuto di \(H_0\) al 10%,
\(0.05<p_\text{value}<0.1\), marginalmente significativo \(\fbox{.}\).
Esempio 15.11 Lanciamo \(n=100\) un moneta di cui non siamo sicuri se è truccata oppure no. Osserviamo 60 successi su 50 lanci. Verificare l’ipotesi che la moneta sia bilanciata (\(\pi=0.5\)), contro l’alternativa che sia maggiore.
Lo stimatore di massima verosimiglianza è \[\hat\pi=\frac 1 n \sum_{i=1}^n X_i\]
Test \(Z\) per una proporzione
La stima \[\hat\pi=\frac { 60 } { 100 }= 0.6 \]
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \pi = \pi_0=0.5 \\ H_1: \pi > \pi_0=0.5 \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\) Test Binomiale per \(n\) grande: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\pi - \pi_{0}} {\sqrt {\pi_0(1-\pi_0)/\,n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 0.6 - 0.5 )} {\sqrt{ 0.5 (1- 0.5 )/ 100 }} = 2 \,. \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
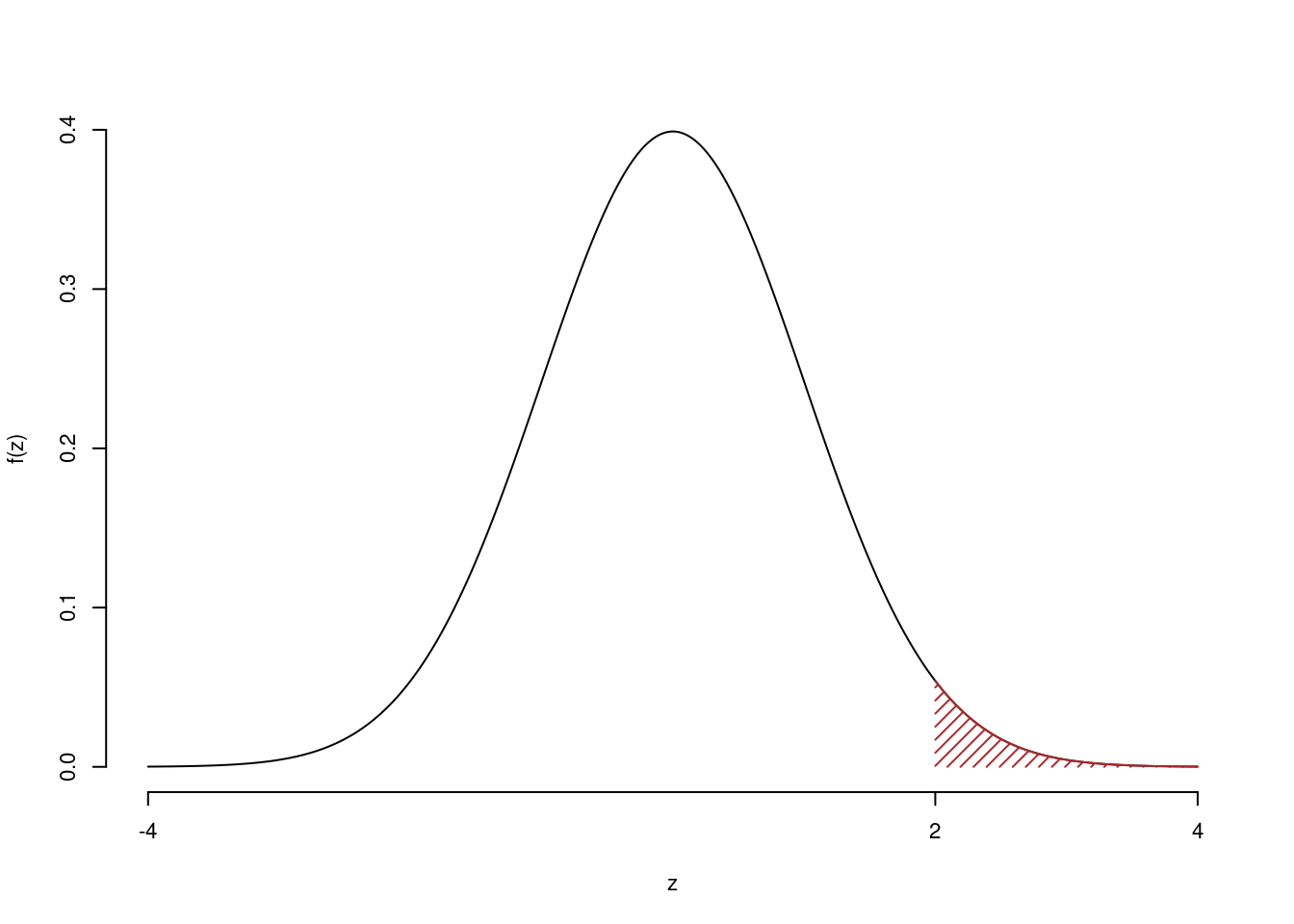
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(Z>2)=0.022750 \]
\[
0.01 < p_\text{value}= 0.022750 \leq 0.05
\]
Rifiuto \(H_0\) al 5%,
\(0.01<p_\text{value}<0.05\), significativo \(\fbox{*}\).
Esempio 15.12 Lanciamo \(n=1000\) un moneta di cui non siamo sicuri se è truccata oppure no. Osserviamo 600 successi su 50 lanci. Verificare l’ipotesi che la moneta sia bilanciata (\(\pi=0.5\)), contro l’alternativa che sia maggiore.
Lo stimatore di massima verosimiglianza è \[\hat\pi=\frac 1 n \sum_{i=1}^n X_i\]
Test \(Z\) per una proporzione
La stima \[\hat\pi=\frac { 600 } { 1000 }= 0.6 \]
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \pi = \pi_0=0.5 \\ H_1: \pi > \pi_0=0.5 \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\) Test Binomiale per \(n\) grande: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\pi - \pi_{0}} {\sqrt {\pi_0(1-\pi_0)/\,n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 0.6 - 0.5 )} {\sqrt{ 0.5 (1- 0.5 )/ 1000 }} = 6.325 \,. \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
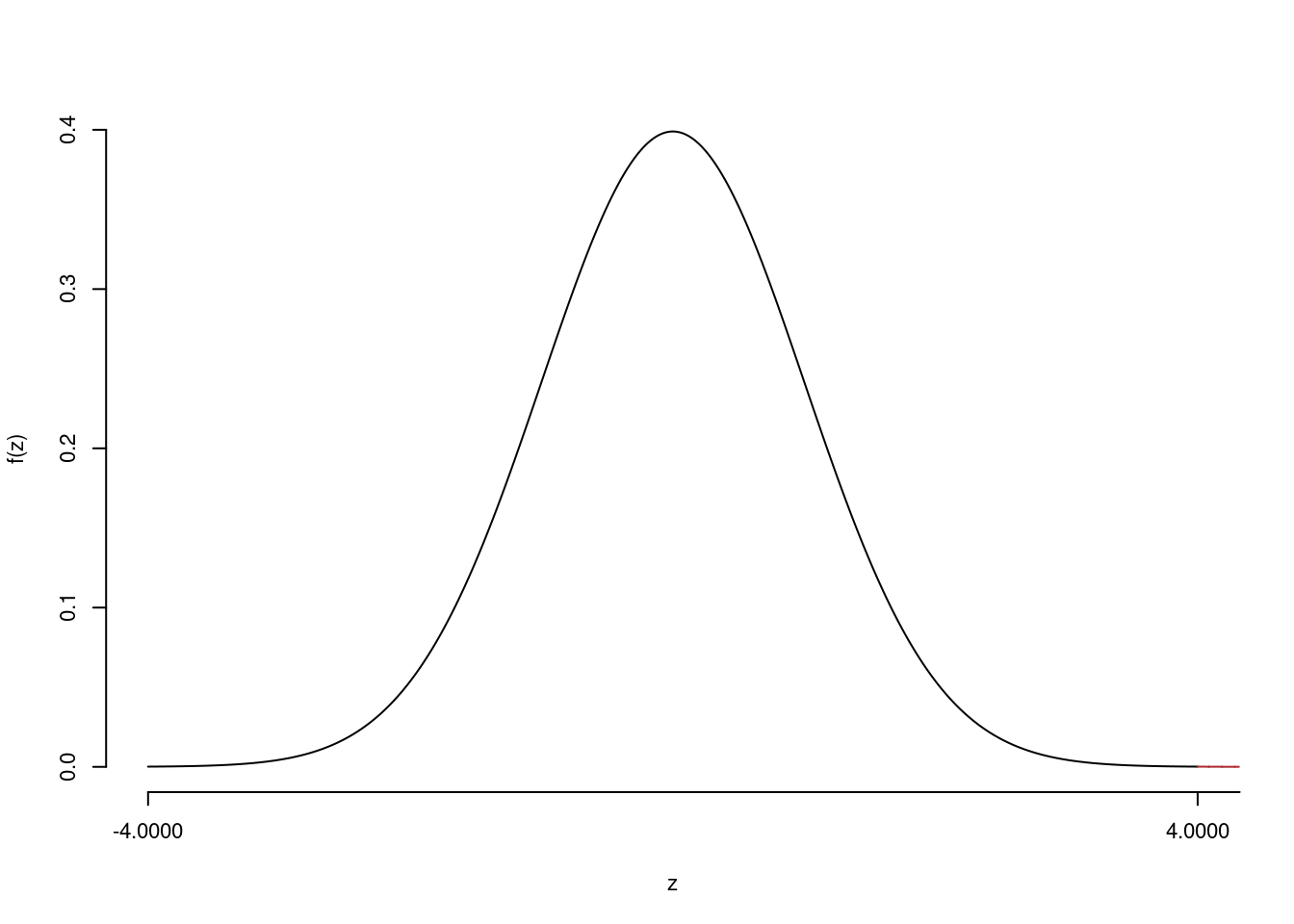
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(Z>6.32)=1e-10 \]
\[
0 < p_\text{value}= 1e-10 \leq 0.001
\]
Rifiuto \(H_0\) sotto all’1‰,
\(p_\text{value}<0.001\), estremamente significativo \(\fbox{***}\).
Esempio 15.13 In una indagine su 100 imprese, si ha che 30 imprese decentrano la lavorazione tipo A. Il censimento precedente aveva rilevato una proporzione di decentramento, \(\pi = 0.4\). Verificare l’ipotesi che il valore osservato sia dovuto al caso, contro l’alternativa che vi sia stata una diminuzione della proporzione di decentramento.
Test \(Z\) per una proporzione
La stima \[\hat\pi=\frac { 30 } { 100 }= 0.3 \]
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \pi = \pi_0=0.4 \\ H_1: \pi < \pi_0=0.4 \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\) Test Binomiale per \(n\) grande: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\pi - \pi_{0}} {\sqrt {\pi_0(1-\pi_0)/\,n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 0.3 - 0.4 )} {\sqrt{ 0.4 (1- 0.4 )/ 100 }} = -2.041 \,. \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
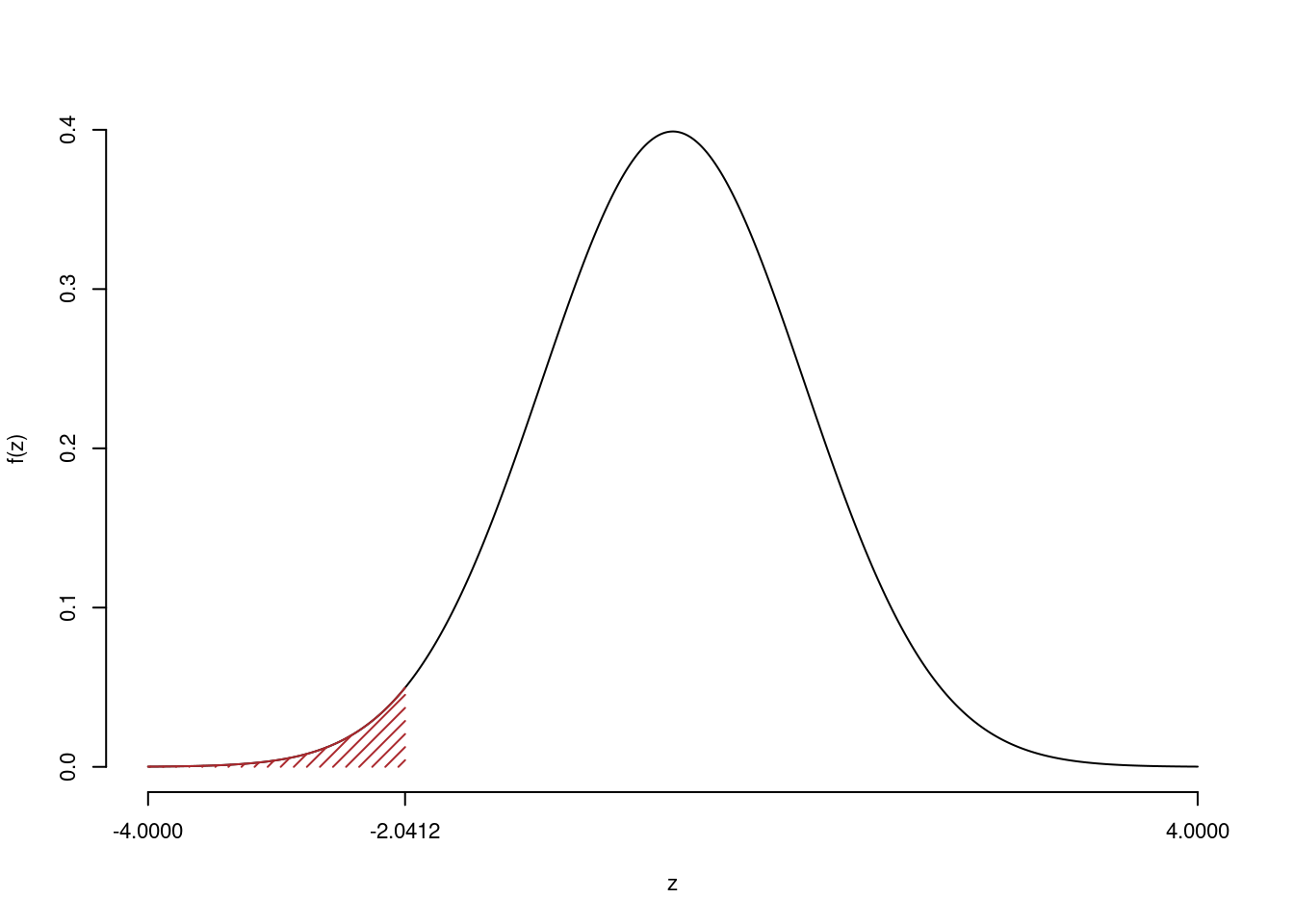
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(Z<-2.04)=0.020613 \]
\[
0.01 < p_\text{value}= 0.020613 \leq 0.05
\]
Rifiuto \(H_0\) al 5%,
\(0.01<p_\text{value}<0.05\), significativo \(\fbox{*}\).
Esempio 15.14 Una città è composta da 50000 soggetti. Si estrae un campione casuale di 100 soggetti e si trova che 20 soggetti possiedono una connessione a banda ultra-larga. La proporzione posseduta a livello nazionale è pari al 25%. Verificare che nella città la percentuale sia diversa (in più o in meno).
Test \(Z\) per una proporzione
La stima \[\hat\pi=\frac { 20 } { 100 }= 0.2 \]
\(\fbox{A}\) FORMULAZIONE DELLE IPOTESI
\[\begin{cases} H_0: \pi = \pi_0=0.25 \\ H_1: \pi \neq \pi_0=0.25 \end{cases}\]
\(\fbox{B}\) SCELTA E CALCOLO STATISTICA-TEST, \(Z\) Test Binomiale per \(n\) grande: \(\Rightarrow\) z-Test.
\[\begin{eqnarray*} \frac{\hat\pi - \pi_{0}} {\sqrt {\pi_0(1-\pi_0)/\,n}}&\sim&N(0,1)\\ z_{\text{obs}} &=& \frac{ ( 0.2 - 0.25 )} {\sqrt{ 0.25 (1- 0.25 )/ 100 }} = -1.155 \,. \end{eqnarray*}\]
\(\fbox{C}\) CONCLUSIONE
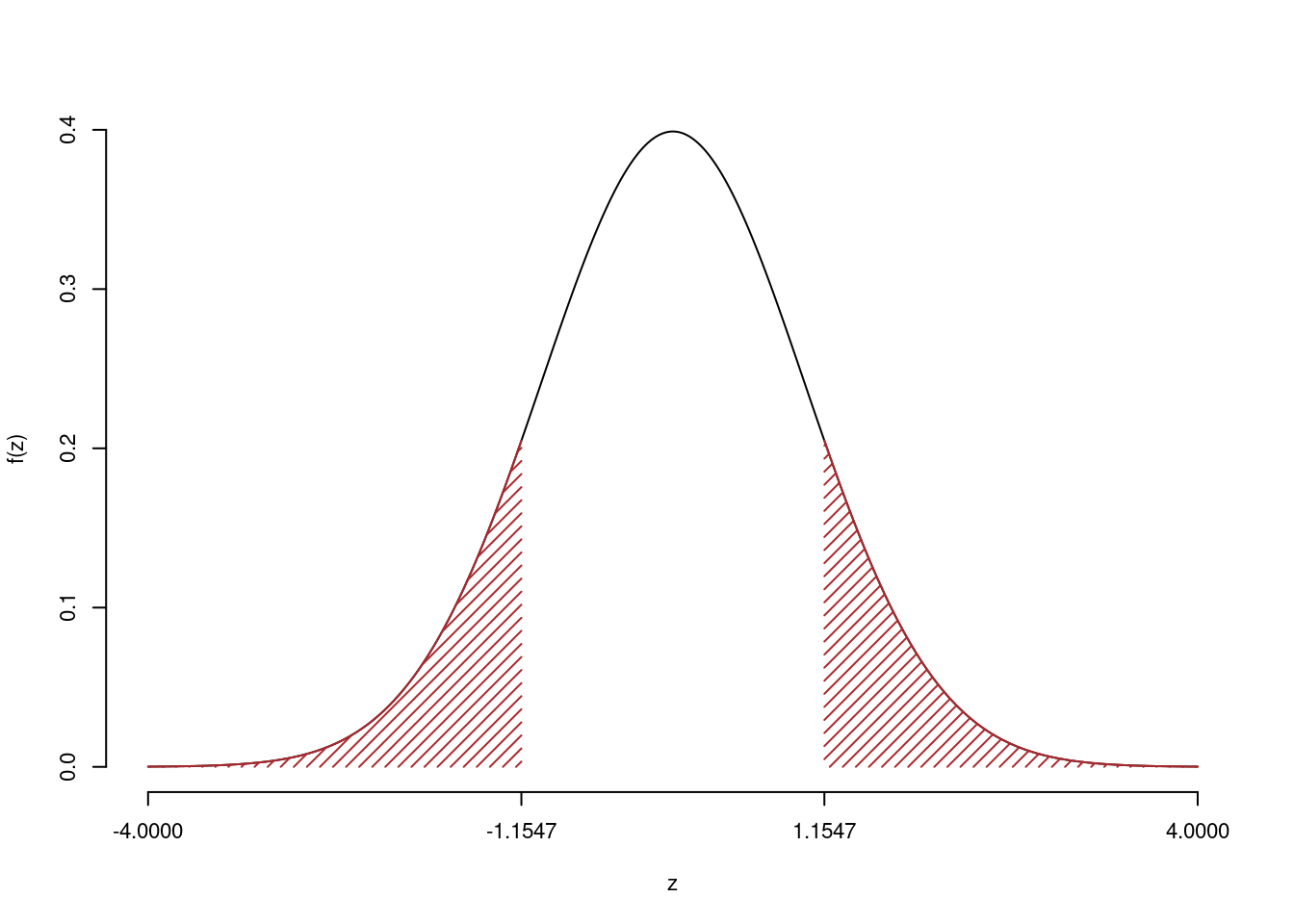
Il \(p_{\text{value}}\) è
\[ p_{\text{value}} = P(|Z|>|-1.15|)=2P(Z>1.15)=0.248213 \]
\[
0.1 < p_\text{value}= 0.248213 \leq 1
\]
Non rifiuto \(H_0\) a nessun livello di significatività,
\(p_\text{value}>0.1\), non significativo
15.6 Specchietto Finale per i Test ad un Campione
\[\begin{align*} \hline H_0:\mu&=\mu_0 &&\text{$\sigma^2$} &\text{Dist.} & && \text{Statistica Test} && \text{Zona Rifiuto} &&p_\text{value}\\ \hline\\ H_1:\mu&>\mu_0 & \text{Noto} && Z && z_\text{obs}&=\frac{\hat \mu-\mu_0}{\sigma/\sqrt{n}} & z_\text{obs}&>z_\alpha & p_\text{value}&= P(Z>z_\text{obs})\\ H_1:\mu&<\mu_0 & \text{Noto} && Z && z_\text{obs}&=\frac{\hat \mu-\mu_0}{\sigma/\sqrt{n}} & z_\text{obs}&<-z_\alpha& p_\text{value}&= P(Z<z_\text{obs})\\ H_1:\mu&\ne\mu_0 & \text{Noto} && Z && z_\text{obs}&=\frac{\hat \mu-\mu_0}{\sigma/\sqrt{n}} & |z_\text{obs}|&>|z_{\alpha/2}| & p_\text{value}&= 2P(Z>|z_\text{obs}|)\\ H_1:\mu&>\mu_0 & \text{Incognito} && t_{n-1} && z_\text{obs}&=\frac{\hat \mu-\mu_0}{S/\sqrt{n}} & t_\text{obs}&>t_{n-1;~\alpha}& p_\text{value}&= P(T>t_\text{obs})\\ H_1:\mu&<\mu_0 & \text{Incognito} && t_{n-1} && z_\text{obs}&=\frac{\hat \mu-\mu_0}{S/\sqrt{n}} & t_\text{obs}&<-t_{n-1;~\alpha}& p_\text{value}&= P(T<t_\text{obs})\\ H_1:\mu&\ne\mu_0 & \text{Incognito} && t_{n-1} && z_\text{obs}&=\frac{\hat \mu-\mu_0}{S/\sqrt{n}} & |t_\text{obs}|&>|t_{n-1;~\alpha/2}|& p_\text{value}&= 2P(T>|t_\text{obs}|)\\ \hline H_0:\pi&=\pi_0 && &\text{Dist.} && &\text{Statistica Test} && \text{Zona Rifiuto} &&p_\text{value}\\ \hline\\ H_1:\pi&>\pi_0 & && Z && z_\text{obs}&=\frac{\hat \pi-\pi_0}{\sqrt{\pi(/1-\pi)}/\sqrt{n}} & z_\text{obs}&>z_\alpha& p_\text{value}&= P(Z>z_\text{obs})\\ H_1:\pi&<\pi_0 & && Z && z_\text{obs}&=\frac{\hat \pi-\pi_0}{\sqrt{\pi(/1-\pi)}/\sqrt{n}} & z_\text{obs}&<-z_\alpha& p_\text{value}&= P(Z<z_\text{obs})\\ H_1:\pi&\ne\pi_0 & && Z && z_\text{obs}&=\frac{\hat \pi-\pi_0}{\sqrt{\pi(/1-\pi)}/\sqrt{n}} & |z_\text{obs}|&>|z_{\alpha/2}| & p_\text{value}&= 2P(Z>|z_\text{obs}|)\\ \hline \end{align*}\]