Capitolo 13 Stima Intervallare
13.1 Obiettivo
Oltre alla stima di un punto specifico \(\hat\theta\) dello spazio dei parametri potremmo essere interessati a trovare regioni più verosimili.
L’obiettivo è di stimare un intervallo nel quale pensiamo verosimilmente si collochi il vero \(\theta\) alla luce dei dati.
Nel gergo dei sondaggisti viene chiamata forbice.
La teoria della verosimiglianza offre tutti gli strumenti per la derivazione coerente di intervalli per una classe molto ampia di modelli di probabilità. La trattazione sistematica attraverso la verosimiglianza esula dagli scopi di questo corso.
13.2 Il Contesto Probabilistico
Siano \(X_1,...X_5\), \(n=5\) VC IID, \(X_i\sim N(\mu=2.5,\sigma^2=2.25)\)
Dalle proprietà della normale \[\frac 1 n \sum_{i=1}^n X_i=\bar X=\hat\mu\sim N\left(\mu,\frac{\sigma^2}{n}\right), \qquad\text{ovvero }\hat \mu\sim N\left(\mu,SE^2(\hat \mu)\right) \]
In questo caso \[\begin{eqnarray*} \hat \mu &\sim& N\left(2.5,\frac{2.25}{5}\right)\\ &\sim& N\left(2.5,\left(\frac{1.5}{\sqrt{5}}\right)^2\right)\\ &\sim& N\left(2.5,0.6708^2\right) \end{eqnarray*}\]
La densità di probabilità di \(\hat \mu\).

13.2.1 Un intervallo per \(\hat \mu\)
Domanda: qual è quel valore \(x^*>0\) tale che \[P(\mu-x^*<\hat \mu<\mu+x^*)=0.95~~?\]

qual è quel numero \(x^*\) tale che \[P(\hat \mu>\mu+x^*)=0.025,\qquad P(\hat \mu < \mu - x^*)=0.025 ~~?\]
Trasferiamo il problema sulla normale standard
Se \(Z\sim N(0,1)\)
Qual è quel numero \(z^*\) tale che \[P(Z>z^*)=0.025 ~~?\]
Dall’ultima riga delle tavole osserviamo che \(z^*=1.96\), infatti \[P(Z>1.96)=1- \Phi(1.96)=1-0.975=0.025 \]
E dunque \[P(-19.6<Z<+1.96)=0.95\]
Ci serviamo delle tavole della Z per \(\hat \mu\), ricordiamo che \(\hat \mu\sim N(\mu,SE^2(\hat \mu))\), allora \[Z=\frac{\hat \mu-\mu}{SE(\hat \mu)}\sim N(0,1)\]
e quindi \[\begin{eqnarray*} P(-1.96<Z<+1.96) &=& 0.95 \\ P\left(-1.96<\frac{\hat \mu -\mu}{SE(\hat \mu)}< +1.96\right) &=& 0.95 \\ P\left(-1.96~SE(\hat \mu)<\hat \mu -\mu< +1.96~SE(\hat \mu)\right) &=& 0.95 \\ P\left(\mu-1.96~SE(\hat \mu)<\mu+\hat \mu -\mu< \mu+1.96~SE(\hat \mu)\right) &=& 0.95 \\ P(\mu-1.96~SE(\hat \mu)<\hat \mu<\mu+1.96~SE(\hat \mu)) &=& 0.95 \end{eqnarray*}\]
Numericamente \[\begin{eqnarray*} P\left(2.5-1.96~\frac{1.5}{\sqrt{5}}<\hat \mu < 2.5+1.96~\frac{1.5}{\sqrt{5}}\right) &=& 0.95 \\ P\left(2.5-1.96\times0.6708<\hat \mu < 2.5+1.96\times0.6708\right) &=& 0.95 \\ P(1.1852 < \hat \mu < 3.8148) &=& 0.95 \end{eqnarray*}\]
13.2.2 \(n\) e \(\sigma^2\) rimangono fissi, cambiamo \(\mu\)
Se \(n=5\) e \(\sigma^2=2.25\), ma per esempio \(\mu= 1.2\) allora \[\begin{eqnarray*} P(\mu-1.96~SE(\hat \mu)<\hat \mu<\mu+1.96~SE(\hat \mu)) &=& 0.95\\ P\left(\mu-1.96~\frac{\sigma}{\sqrt n}<\hat \mu < \mu+1.96~\frac{\sigma}{\sqrt n}\right) &=& 0.95 \\ P\left(1.2-1.96~\frac{1.5}{\sqrt{5}}<\hat \mu < 1.2+1.96~\frac{1.5}{\sqrt{5}}\right) &=& 0.95 \\ P\left(1.2-1.96\times0.6708<\hat \mu < 1.2+1.96\times0.6708\right) &=& 0.95 \\ P(-0.1148 < \hat \mu < 2.5148) &=& 0.95 \end{eqnarray*}\]
Se \(n=5\) e \(\sigma^2=2.25\), ma per esempio \(\mu= 3.4\) allora \[\begin{eqnarray*} P\left(3.4-1.96~\frac{1.5}{\sqrt{5}}<\hat \mu < 3.4+1.96~\frac{1.5}{\sqrt{5}}\right) &=& 0.95 \\ P\left(3.4-1.96\times0.6708<\hat \mu < 3.4+1.96\times0.6708\right) &=& 0.95 \\ P(2.0852 < \hat \mu < 4.7148) &=& 0.95 \end{eqnarray*}\]
Se \(n=5\) e \(\sigma^2=2.25\), ma per esempio \(\mu= 0.6\) allora \[\begin{eqnarray*} P\left(0.6-1.96\times0.6708<\hat \mu < 0.6+1.96\times0.6708\right) &=& 0.95 \\ P(-0.7148 < \hat \mu < 1.9148) &=& 095 \end{eqnarray*}\]
Rimangono fissi \(n\) e \(\sigma^2\) , cambiamo \(\mu\)

13.2.3 \(n\) e \(\sigma^2\) rimangono fissi e noti, \(\mu\) incognita \(\hat \mu=2.6\)
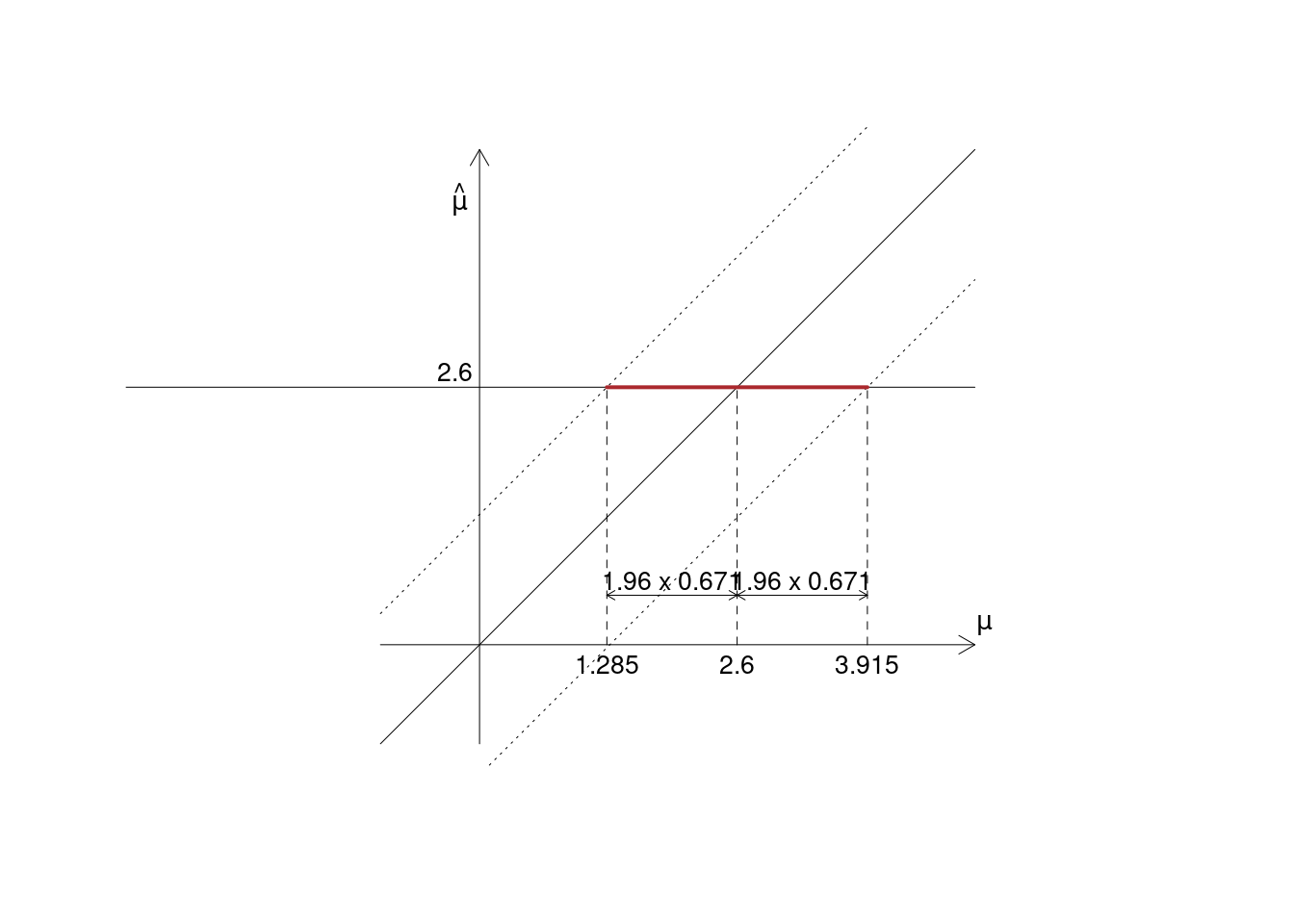
Algebricamente, osserviamo \[\begin{eqnarray*} P(-1.96<Z<+1.96) &=& 0.95 \\ P\left(-1.96<\frac{\hat \mu -\mu}{SE(\hat \mu)}< +1.96\right) &=& 0.95 \\ P\left(- 1.96~SE(\hat \mu)<\hat \mu-\mu<+1.96~SE(\hat \mu)\right) &=& 0.95\\ P\left( - 1.96~\frac\sigma{\sqrt n}<\hat \mu-\mu<\mu+1.96~\frac\sigma{\sqrt n}\right) &=& 0.95\\ P\left(-\hat \mu - 1.96~\frac\sigma{\sqrt n}< -\hat \mu+\hat \mu-\mu<-\hat \mu+1.96~\frac\sigma{\sqrt n}\right) &=& 0.95 \qquad\text{sottraggo $\hat \mu$}\\ P\left(-\hat \mu- 1.96~\frac\sigma{\sqrt n}<-\mu<-\hat \mu+1.96~\frac\sigma{\sqrt n}\right) &=& 0.95\\ \left(+\hat \mu+ 1.96~\frac\sigma{\sqrt n}>+\mu>+\hat \mu-1.96~\frac\sigma{\sqrt n}\right) &=& 0.95\qquad\text{cambio segno e verso}\\ P\left(\hat \mu- 1.96~\frac\sigma{\sqrt n}<\mu<\hat \mu+1.96~\frac\sigma{\sqrt n}\right) &=& 0.95\\ \end{eqnarray*}\]
13.3 Intervalli casuali
\[ P\left(\hat \mu- 1.96~\frac\sigma{\sqrt n}<\mu<\hat \mu+1.96~\frac\sigma{\sqrt n}\right) = 0.95\] non è la probabilità che \(\mu\) si trovi tra \(\hat \mu- 1.96~\frac\sigma{\sqrt n}\) e \(\hat \mu+ 1.96~\frac\sigma{\sqrt n}\),
\[ P\left(\hat \mu- 1.96~\frac\sigma{\sqrt n}<\mu<\hat \mu+1.96~\frac\sigma{\sqrt n}\right) = 0.95\] è la probabilità che l’intervallo casuale \(\left[\hat \mu- 1.96~\frac\sigma{\sqrt n},\hat \mu+ 1.96~\frac\sigma{\sqrt n}\right]\) cada su \(\mu\).
Se quindi \(\hat \mu = 2.6\) l’intervallo \[\begin{eqnarray*} \left[\hat \mu- 1.96~\frac\sigma{\sqrt n},\hat \mu+ 1.96~\frac\sigma{\sqrt n}\right] &=& \left[2.6- 1.96~\frac{1.5}{\sqrt 5},\hat \mu+ 1.96~\frac{1.5}{\sqrt 5}\right]\\ &=& \left[1.2852,3.9148\right] \end{eqnarray*}\]
L’intervallo \(\left[1.2852,3.9148\right]\) è una realizzazione dell’intervallo casuale \(\left[\hat \mu- 1.96~\frac\sigma{\sqrt n},\hat \mu+ 1.96~\frac\sigma{\sqrt n}\right]\).
13.4 Intervallo di confidenza per \(\mu\) al 95%, \(n=5\) e \(\sigma^2=2.25\).
Se \(\hat \mu = 2.6\) l’intervallo \[\begin{eqnarray*} \left[\hat \mu- 1.96~\frac\sigma{\sqrt n},\hat \mu+ 1.96~\frac\sigma{\sqrt n}\right] &=& \left[2.6- 1.96~\frac{1.5}{\sqrt 5},\hat \mu+ 1.96~\frac{1.5}{\sqrt 5}\right]\\ &=& \left[1.2852,3.9148\right]\\ \end{eqnarray*}\] è chiamato intervallo di confidenza per \(\mu\) al 95%.
Infelice traduzione di Confidence Interval,
- to be confident that the real parameter is in \(\left[1.2852,3.9148\right]\), with a confidence level of 95%.
- Siamo fiduciosi che il vero parametro si trovi in \(\left[1.2852,3.9148\right]\), con un livello di fiducia del 95%
L’intervallo è costruito con una metodologia che 95 volte su 100 produce intervalli che coprono il vero \(\mu\). Il long run:
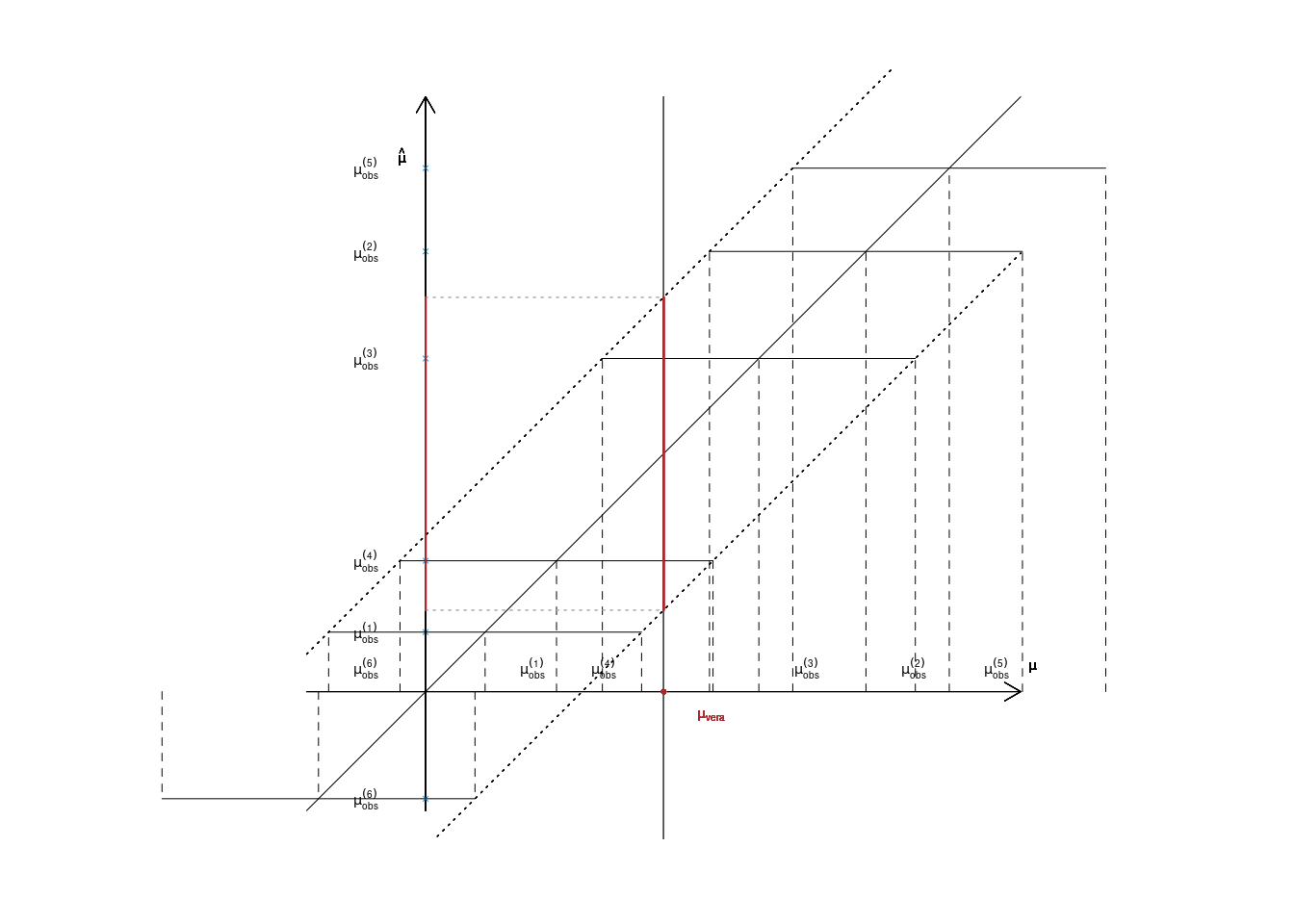
13.5 Stimatori e intervalli di confidenza
Se \(\theta\) è il parametro da stimare uno stimatore puntuale \(h\) è una VC \[h(X_1,...,X_n)=h=\hat\theta\]
Siano \(L_1(X_1,...,X_n)=L_1\) e \(L_2(X_1,...,X_n)=L_2\) due statistiche tali che \(L_1\leq L_2\) per ogni campione \(X_1,...,X_n\). L’intervallo \[[L_1,L_2]\] è un intervallo casuale.
Definizione 13.1 Un intervallo di confidenza per \(\theta\) al livello \((1-\alpha)\times 100\%\) è costruito su quella coppia di statistiche \(L_1\) e \(L_2\) tali che \[P(L_1<\theta<L_2)=1-\alpha\]
Un intervallo di confidenza per \(\theta\) al livello \((1-\alpha)\times 100\%\) è l’intervallo \([L_1,L_2]\) calcolato sui dati del campione.
13.6 Massima Verosimiglianza e intervalli di confidenza
Se \(\hat\theta\) è lo stimatore di massima verosimiglianza per \(\theta\), se \(n\) è sufficientemente alto \[\hat\theta\operatorname*{\sim}_a N(\theta,\widehat{SE^2(\hat\theta)}\equiv I^{-1}(\theta))\]
L’intervallo di confidenza per \(\theta\) al livello \((1-\alpha)\times 100\%\) è ricavato da: \[P(\hat\theta-z_{\alpha/2}\widehat{SE(\hat\theta)}<\theta<\hat\theta+z_{\alpha/2}\widehat{SE(\hat\theta)})=1-\alpha\]
Un intervallo di confidenza per \(\theta\) al livello \((1-\alpha)\times 100\%\) è l’intervallo \([\hat\theta-z_{\alpha/2}\widehat{SE(\hat\theta)},\hat\theta+z_{\alpha/2}\widehat{SE(\hat\theta)}]\) calcolato sui dati del campione.
13.7 Intervalli di Confidenza per \(\mu\) al livello \((1-\alpha)\times 100\), \(\sigma^2\) nota
Sia \(0<\alpha<1\), osserviamo che \[\begin{eqnarray*} P(-z_{\alpha/2}<Z<+z_{\alpha/2}) &=& 1-\alpha \\ P\left(-z_{\alpha/2}<\frac{\hat \mu -\mu}{SE(\hat \mu)}< +z_{\alpha/2}\right) &=& 1-\alpha \\ P\left(\hat \mu- z_{\alpha/2}~\frac\sigma{\sqrt n}<\mu<\hat \mu+z_{\alpha/2}~\frac\sigma{\sqrt n}\right) &=& 1-\alpha \end{eqnarray*}\]
Definizione 13.2 (Intervallo di Confidenza per $\mu$ ($\sigma^2$ nota)) Si definisce L’IdC al livello \((1-\alpha)\times100\%\) per \(\mu\) con \(\sigma^2\) nota, l’intervallo \[IdC:~~\left[\hat \mu- z_{\alpha/2}~\frac\sigma{\sqrt n},\hat \mu+ z_{\alpha/2}~\frac\sigma{\sqrt n}\right]\]
Dove \(z_{\alpha/2}\) è quel valore tale che \(P(Z>z_{\alpha/2})=\alpha/2\)
\[ P\left(\hat \mu- z_{\alpha/2}~\frac\sigma{\sqrt n}<\mu<\hat \mu+z_{\alpha/2}~\frac\sigma{\sqrt n}\right) = 1-\alpha\] è la probabilità che l’intervallo casuale \(\left[\hat \mu- z_{\alpha/2}~\frac\sigma{\sqrt n},\hat \mu+ z_{\alpha/2}~\frac\sigma{\sqrt n}\right]\) cada su \(\mu\).
Il valore \(0<\alpha<1\), può essere qualunque ma solitamente si usa
- \(\alpha=0.05\): intervalli al \((1-0.05)\times 100\%=0.95\times 100\%=95\%\)
- \(\alpha=0.01\): intervalli al \((1-0.01)\times 100\%=0.99\times 100\%=99\%\)
- Gli intervalli per \(\alpha=0.1\) e \(\alpha=0.001\), intervalli al \(90\%\) e al \(99.9\%\) meno usati.
| \(\alpha\) | \(\alpha/2\) | \(z_{\alpha/2}\) | ||
|---|---|---|---|---|
| \(\alpha=0.1\) | con \(\alpha/2=0.05\) | e quindi \(z_{\alpha/2}=z_{0.05}\) | \(=1.6449\) | Raro |
| \(\alpha=0.05\) | con \(\alpha/2=0.025\) | e quindi \(z_{\alpha/2}=z_{0.025}\) | \(=1.96\) | Freq. |
| \(\alpha=0.01\) | con \(\alpha/2=0.005\) | e quindi \(z_{\alpha/2}=z_{0.005}\) | \(=2.5758\) | Freq. |
| \(\alpha=0.001\) | con \(\alpha/2=0.0005\) | e quindi \(z_{\alpha/2}=z_{0.005}\) | \(=3.2905\) | Raro |
Esempio 13.1 Intervallo al 99%, \(\hat \mu=2.6\), \(n=5\), \(\sigma^2=2.25\). L’intervallo al 99% implica un \(\alpha=0.01\), infatti \[1-\alpha=0.99\]
E dunque \[\alpha/2=0.005\]
Dalle tavole \[z_{\alpha/2}=z_{0.005}=2.5758\]
Se quindi \(\hat \mu = 2.6\) l’intervallo \[\begin{eqnarray*} \left[\hat \mu- 2.5758~\frac\sigma{\sqrt n},\hat \mu+ 2.5758~\frac\sigma{\sqrt n}\right] &=& \left[2.6- 2.5758~\frac{1.5}{\sqrt 5},2.6+ 2.5758~\frac{1.5}{\sqrt 5}\right]\\ &=& \left[0.8721,4.3279\right] \end{eqnarray*}\]
È l’intervallo di confidenza per \(\mu\) al \(99\%\)
Esempio 13.2 Intervallo al \(99\%\), \(\hat \mu=2.6\), \(n=5\), \(\sigma^2=2.25\). L’intervallo al 90% implica un \(\alpha=0.1\), infatti \[1-\alpha=0.90\]
E dunque \[\alpha/2=0.05\]
Dalle tavole \[z_{\alpha/2}=z_{0.05}=1.6449\]
Se quindi \(\hat \mu = 2.6\) l’intervallo \[\begin{eqnarray*} \left[\hat \mu- 1.6449~\frac\sigma{\sqrt n},\hat \mu+ 1.6449~\frac\sigma{\sqrt n}\right] &=& \left[2.6- 1.6449~\frac{1.5}{\sqrt 5},2.6+ 1.6449~\frac{1.5}{\sqrt 5}\right]\\ &=& \left[1.4966,3.7034\right] \end{eqnarray*}\]
È l’intervallo di confidenza per \(\mu\) al \(90\%\).
Osserviamo graficamente gli intervalli di confidenza per \(\mu\) con \(\hat \mu=2.6\), \(n=5\) e \(\sigma^2=2.25\), al 90%, 95%, 99% e 99.9%.
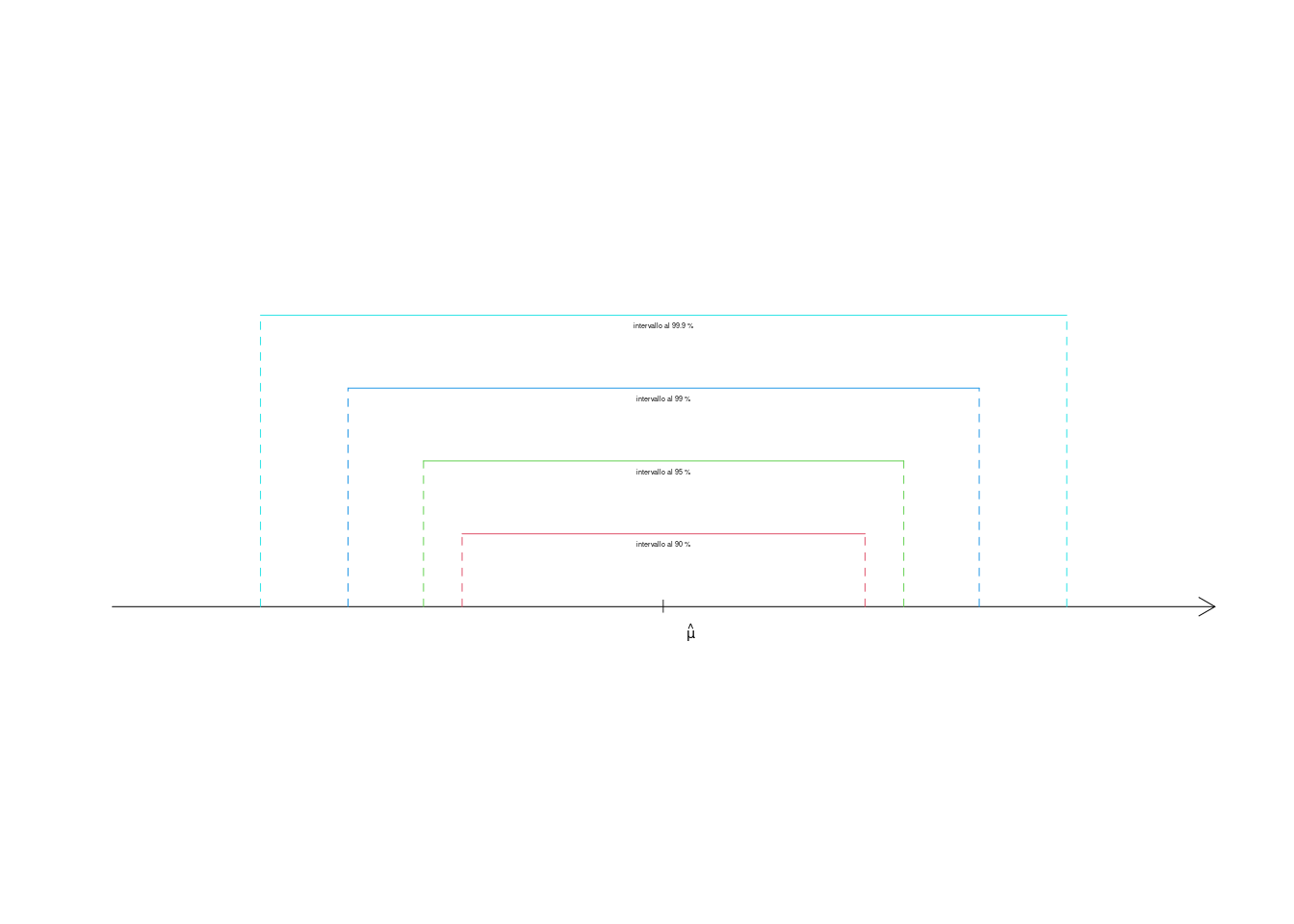
| \(\alpha=0.1\) | \(\alpha=0.05\) | \(\alpha=0.01\) | \(\alpha=0.001\) | |
|---|---|---|---|---|
| \(\hat \mu - z_{\alpha/2}SE(\hat \mu)\) | 1.497 | 1.285 | 0.8721 | 0.3926 |
| \(\hat \mu + z_{\alpha/2}SE(\hat \mu)\) | 3.703 | 3.915 | 4.3279 | 4.8074 |
| Ampiezza | 2.207 | 2.630 | 3.4558 | 4.4147 |
Esempio 13.3 Un venditore di bustine di tè assicura che ogni bustina ha un peso medio pari a 20g con una SD pari a 1.5g. L’acquirente esegue 6 misure di controllo e ottiene i seguenti risultati: 19; 20; 20.5; 21; 18.5; 15. La media di questi numeri è \(\hat\mu = 19\) e \(\widehat{\sigma}=1.979\). Determinare un IdC al livello di \((1-\alpha)=0.99\) per \(\mu\).
\[\begin{eqnarray*} & & \left[\hat\mu -z_{\alpha/2} \frac{\sigma} {\sqrt{n}}; \hat\mu +z_{\alpha/2} \frac{\sigma} {\sqrt{n}} \right] \\ &=& \left[ 19 -2.576 \frac{1.5} {\sqrt{6}}; 19 +2.576 \frac{1.5} {\sqrt{6}} \right] \\ &=& \left[ 19 - 1.5775; 19 + 1.5775 \right] \\ &=& \left[ 17.4225;\quad 20.5775 \right] \end{eqnarray*}\]
Notare la modalità di indicare la SD della \(\cal{P}\) e dei dati. Vi sono due informazioni su \(\sigma\) e bisogna scegliere quella giusta.
13.8 Intervalli di Confidenza per \(\mu\) al livello \((1-\alpha)\times 100\), \(\sigma^2\) incognita
Se \(\sigma^2\) è incognito va stimato dai dati
Consideriamo lo stimatore \(S^2\) di \(\sigma^2\) \[S^2=\frac {1}{n-1}\sum_{i=1}^n (X_i-\hat \mu)^2=\frac {n}{n-1}\frac 1 n\sum_{i=1}^n (X_i-\hat \mu)^2=\frac n {n-1}\hat\sigma^2\]
Ricordiamo che \[\widehat{SE(\hat\mu)}=\sqrt{\frac {S^2}n}=\frac S {\sqrt n}\]
Ricordiamo infine che \[T=\frac{\hat \mu-\mu}{\widehat{SE(\hat\mu)}}\sim t_{n-1}\]
Ovvero \[T=\frac{\hat \mu-\mu}{S/\sqrt n}\sim t_{n-1}\]
13.8.1 \(\sigma\) nota e \(\sigma\) incognita
Se \(\sigma\) è nota \[Z=\frac{\hat \mu-\mu}{\sigma/\sqrt n}\sim N(0,1)\]
Se \(\sigma\) è incognita \[T=\frac{\hat \mu-\mu}{S/\sqrt n}\sim t_{n-1}\]
Sia \(0<\alpha<1\), osserviamo che \[\begin{eqnarray*} P(-t_{n-1;\alpha/2}<T<+t_{n-1;\alpha/2}) &=& 1-\alpha \\ P\left(-t_{n-1;\alpha/2}<\frac{\hat \mu -\mu}{\widehat{SE(\hat \mu)}}< +t_{n-1;\alpha/2}\right) &=& 1-\alpha \\ P\left(\hat \mu- t_{n-1;\alpha/2}~\frac S{\sqrt n}<\mu<\hat \mu+t_{n-1;\alpha/2}~\frac S{\sqrt n}\right) &=& 1-\alpha \end{eqnarray*}\]
Dove \(t_{n-1;\alpha/2}\) è quel valore tale che \(P(T>t_{n-1;\alpha/2})=\alpha/2,\qquad T\sim t_{n-1}\)
Definizione 13.3 (Intervallo di Confidenza per $\mu$ ($\sigma^2$ incognita)) Si definisce L’IdC al livello \((1-\alpha)\times100\%\) per \(\mu\) con \(\sigma^2\) incognita, l’intervallo \[IdC:~~\left[\hat \mu- t_{n-1;\alpha/2}~\frac S{\sqrt n},\hat \mu+ t_{n-1;\alpha/2}~\frac S{\sqrt n}\right]\]
\[ P\left(\hat \mu- t_{n-1;\alpha/2}~\frac S{\sqrt n}<\mu<\hat \mu+t_{n-1;\alpha/2}~\frac S{\sqrt n}\right) = 1-\alpha\] è la probabilità che l’intervallo casuale \(\left[\hat \mu- t_{n-1;\alpha/2}~\frac S{\sqrt n},\hat \mu+ t_{n-1;\alpha/2}~\frac S{\sqrt n}\right]\) cada su \(\mu\).
Esempio 13.4 Un venditore di bustine di tè assicura che ogni bustina ha un peso medio pari a 20g. L’acquirente esegue 6 misure di controllo e ottiene i seguenti risultati: 19; 20; 20.5; 21; 18.5; 15. La media di questi numeri è \(\hat\mu = 19\) e \(\widehat{\sigma}=1.979\). Determinare un IdC al livello di \((1-\alpha)=0.99\) per \(\mu\).
\[\alpha=0.01\qquad \alpha/2=0.005,\qquad t_{6-1;0.005}=4.0321\]
\[\begin{eqnarray*} & & S = \sqrt{\frac{n} {n-1}} \widehat{\sigma} = \sqrt{\frac{6} {6-1}} 1.979 = 2.1679 \\ & & \left[\hat\mu -t_{(n-1); \alpha/2} \frac{S} {\sqrt{n}}; \hat\mu +t_{(n-1); \alpha/2} \frac{S} {\sqrt{n}} \right] \\ &=& \left[ 19 -4.0321 \frac{2.1679} {\sqrt{6}}; 19 +4.0321 \frac{2.1679} {\sqrt{6}} \right] \\ &=& \left[ 19 - 3.5687;~ 19 + 3.5687 \right] \\ &=& \left[ 15.4313; 22.5687 \right] \end{eqnarray*}\]
Si noti che la mancanza di informazioni sulla varianza rende più incerto il risultato; infatti, la lunghezza dell’IdC aumenta.
Esempio 13.5 Si sono rilevati i tempi dedicati a ciascun cliente da un impiegato di banca in 49 casi e si è ottenuta una media \(\bar{x}=3.5\) minuti con una SD pari a 0.5 minuti. Determinare un IdC al livello di \((1-\alpha)=0.95\) per \(\mu\).
\[\alpha=0.05\qquad \alpha/2=0.025.\qquad t_{49-1;0.025}=2.0106\]
\[\begin{eqnarray*} & & s = \sqrt{\frac{n} {n-1}} \widehat{\sigma} = \sqrt{\frac{49} {49-1}} 0.5 = 0.505 \\ & & \left[\bar{X} -t_{(n-1); \alpha/2} \frac{S} {\sqrt{n}}; \bar{X} +t_{(n-1); \alpha/2} \frac{S} {\sqrt{n}} \right] \\ &=& \left[ 3.5 -2.0106 \frac{0.505} {\sqrt{49}}; 3.5 +2.0106 \frac{0.505} {\sqrt{49}} \right] \\ &=& \left[ 3.5 - 0.145; 3.5 + 0.145 \right] \\ &=& \left[ 3.355; 3.645 \right] \end{eqnarray*}\]
Si noti che per \(n>120\) si può approssimare con una normale.
13.9 IDC per la proporzione
\(X_{1}, \ldots, X_{n}\) VC IID, tutte \(\text{Ber}(\pi)\). Per il TLC \[\bar{X} = \hat\pi \operatorname*{\sim}_a N\left( \pi;\, \frac{\pi (1-\pi)} {n} \right) \Rightarrow \hat\pi \operatorname*{\sim}_a N\left( \pi; SE^2(\hat\pi)\right)\]
E quindi \[Z = \frac{\hat\pi - \pi} {SE(\hat\pi)} \operatorname*{\sim}_a N(0,1) \Rightarrow P\left(-z_{\alpha/2} < \frac{\hat\pi - \pi} {SE(\hat\pi)} < z_{\alpha/2} \right) = 1-\alpha \]
Infine \[\begin{eqnarray*} P\left(\hat\pi -z_{\alpha/2} {SE(\hat\pi)} < \pi <\hat\pi +z_{\alpha/2} {SE(\hat\pi)} \right) &=& 1-\alpha \\ P\left(\hat\pi -z_{\alpha/2} \sqrt{\frac{\pi(1-\pi)}{n}} < \pi <\hat\pi +z_{\alpha/2} \sqrt{\frac{\pi(1-\pi)}{n}} \right) &=& 1-\alpha \end{eqnarray*}\]
l’IdC DIPENDE da \(\pi\) NON NOTA. Per il TLC e \(n\) sufficientemente grande si può sostituire a \(\pi\) dell’IdC la sua stima \(\hat\pi\). \[\widehat{SE(\hat\pi)}=\sqrt\frac{\hat\pi(1-\hat\pi)}{n}\]
Condizioni per l’approssimazione \[n\, \pi \ge 5 \quad\text{e}\quad n\, (1-\pi) \ge 5\]
e quindi l’IdC al livello \((1-\alpha)\times 100\) per \(\hat\pi\) è:
Definizione 13.4 (Intervallo di Confidenza per $\pi$) Si definisce L’IdC al livello \((1-\alpha)\times100\%\) per \(\pi\) l’intervallo \[\left[\,\hat\pi-z_{\alpha/2}\sqrt\frac{\hat\pi(1-\hat\pi)}{n};\hat\pi+z_{\alpha/2}\sqrt\frac{\hat\pi(1-\hat\pi)}{n}\,\right]\]
Esempio 13.6 Una indagine sulle intenzioni di voto degli italiani per lo schieramento \(A\) ha mostrato che 240 su 500 lo voterebbero. Determinare un IdC al livello di \((1-\alpha)=0.99\) per \(\pi\). \[\alpha=0.01,\qquad \alpha/2=0.005,\qquad z_{0.005}=2.5758\]
\[\begin{eqnarray*} & & \hat\pi = \frac{\mbox{favorevoli}} {n} = \frac{240} {500} = 0.48 \\ & & \left[\hat\pi -z_{\alpha/2} \sqrt{\frac{\hat\pi (1-\hat\pi)} {n}}; \hat\pi +z_{\alpha/2} \sqrt{\frac{\hat\pi (1-\hat\pi)} {n}} \right] \\ &=& \left[ 0.48 -2.576 \sqrt{\frac{0.48 (1-0.48)} {500}}; 0.48 +2.576 \sqrt{\frac{0.48 (1-0.48)} {500}} \right] \\ &=& \left[ 0.48 - 0.0576; 0.48 + 0.0576\right] \\ &=& \left[ 0.4224; 0.5376 \right] \end{eqnarray*}\]
Esempio 13.7 Una indagine sulle intenzioni di voto degli italiani per lo schieramento \(A\) ha mostrato che 2400 su 5000 lo voterebbero. Determinare un IdC al livello di \((1-\alpha)=0.99\) per \(\pi\).
\[\begin{eqnarray*} & & \hat\pi = \frac{\mbox{favorevoli}} {n} = \frac{2400} {5000} = 0.48 \\ & & \left[\hat\pi -z_{\alpha/2} \sqrt{\frac{\hat\pi (1-\hat\pi)} {n}}; \hat\pi +z_{\alpha/2} \sqrt{\frac{\hat\pi (1-\hat\pi)} {n}} \right] \\ &=& \left[ 0.48 -2.576 \sqrt{\frac{0.48 (1-0.48)} {5000}}; 0.48 +2.576 \sqrt{\frac{0.48 (1-0.48)} {5000}} \right] \\ &=& \left[ 0.48 - 0.0182; 0.48 + 0.0182\right] \\ &=& \left[ 0.4618; 0.4982 \right] \end{eqnarray*}\]
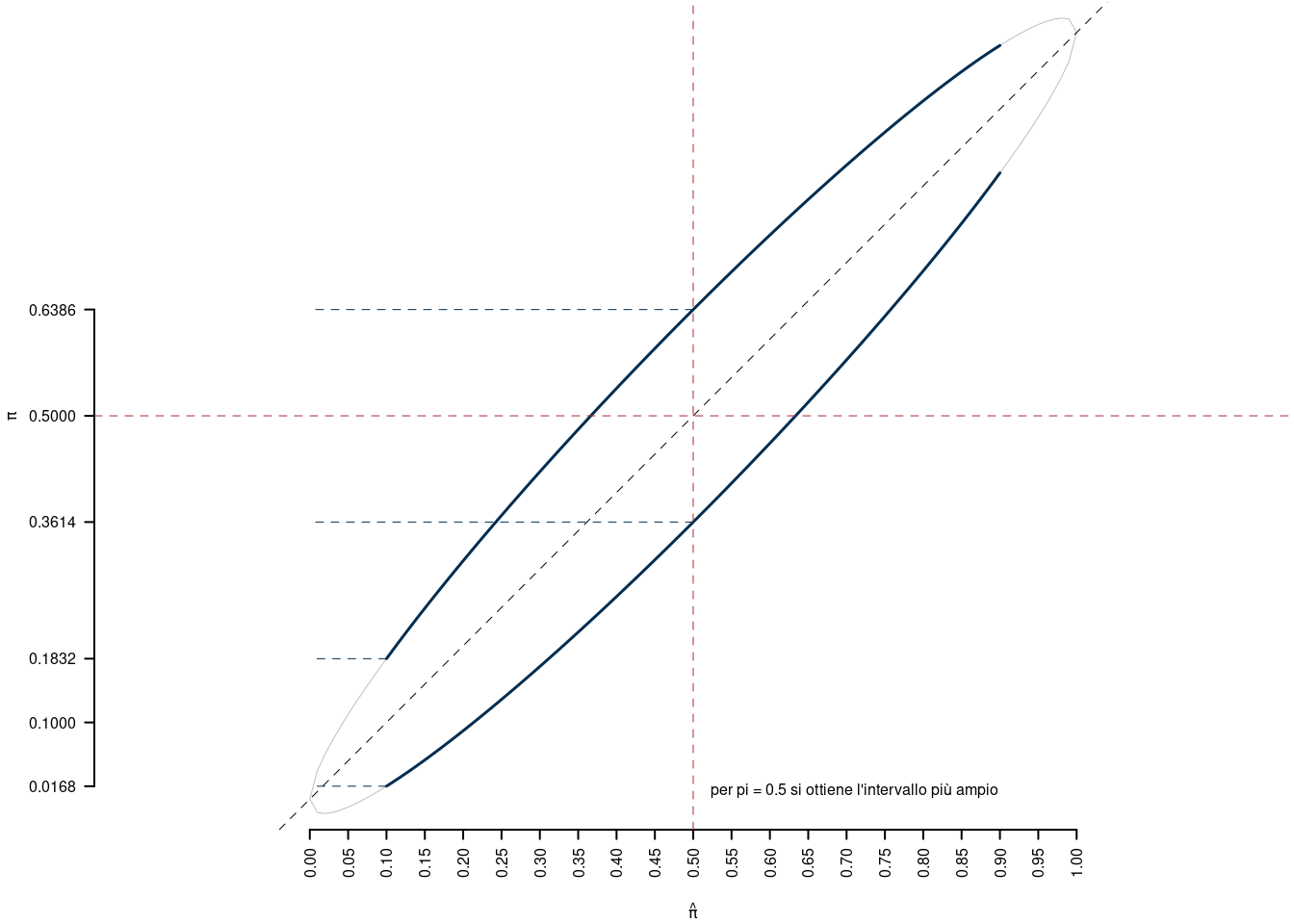
13.9.1 IdC per \(\pi\) per \(\alpha\) ed \(n\) fissati
Se fissiamo \(\alpha\) ed \(n\), per esempio \(\alpha=0.05\) ed \(n=50\), possiamo variare \(S_n\in\{0,...,n\}\) e quindi \(\hat\pi\in{0/n,1/n,...,n/n}\). Per ogni valore di \(\hat\pi\) calcoliamo l’IdC al livello \((1-\alpha)\) e rappresentiamo graficamente
13.10 Specchietto Finale per gli IdC
- Si definisce L’IdC al livello \((1-\alpha)\times100\%\) per \(\mu\) con \(\sigma^2\) nota, l’intervallo \[IdC:~~\left[\hat \mu- z_{\alpha/2}~\frac\sigma{\sqrt n},\hat \mu+ z_{\alpha/2}~\frac\sigma{\sqrt n}\right]\]
- Si definisce L’IdC al livello \((1-\alpha)\times100\%\) per \(\mu\) con \(\sigma^2\) incognita, l’intervallo \[IdC:~~\left[\hat \mu- t_{n-1;\alpha/2}~\frac S{\sqrt n},\hat \mu+ t_{n-1;\alpha/2}~\frac S{\sqrt n}\right]\]
- Si definisce L’IdC al livello \((1-\alpha)\times100\%\) per \(\pi\) l’intervallo \[\left[\,\hat\pi-z_{\alpha/2}\sqrt\frac{\hat\pi(1-\hat\pi)}{n};\hat\pi+z_{\alpha/2}\sqrt\frac{\hat\pi(1-\hat\pi)}{n}\,\right]\]