Capitolo 8 Il Teorema del Limite Centrale

8.1 Successioni di VC

Una successione di variabili casuali è espressa da un numero infinito di variabili casuali \(\{X_1,X_2,...,X_n,...\}\).

Esempio 8.1 Sia \[\begin{eqnarray*} X_1 &\sim& N\left(0,1\right)\\ X_2 &\sim& N\left(0,\frac 12\right)\\ X_3 &\sim& N\left(0,\frac 13\right)\\ ...\\ X_n &\sim& N\left(0,\frac 1n\right)\\ ... \end{eqnarray*}\]

Esempio 8.2 Sia \[\begin{eqnarray*} X_1 &\sim& \text{Binom}\left(1,\pi\right)\\ X_2 &\sim& \text{Binom}\left(2,\pi\right)\\ ...\\ X_n &\sim& \text{Binom}\left(n,\pi\right)\\ ... \end{eqnarray*}\]

Siamo interessati a sapere se la successione converge ad una VC \(X\). Ma essendo VC e non numeri il concetto di convergenza è più complesso. Esistono diversi tipi di convergenza e non entreremo nella trattazione sistematica del tema. Mostreremo solo le convergenze che ci interessano per sviluppare il resto della teoria.

Definizione 8.1 (Convergenza in Distribuzione) Si dice che la successione \(\{X_1,X_2,...,X_n,...\}\) converge in distribuzione alla VC X se e solo se \[\lim_{n\to\infty}F_n(x)=F(x),~\forall x\in S_X\] dove \(F_n\) e \(F\) rappresentano la funzione di ripartizione di \(X_n\) e di \(X\), rispettivamente. E si scrive \[X_n\operatorname*{\rightarrow}_{d} X\]

Definizione 8.2 (Convergenza in Probabilità) Si dice che la successione \(\{X_1,X_2,...,X_n,...\}\) converge in probabilità alla VC X se e solo se \[\lim_{n\to\infty}P(|X_n-X|<\varepsilon)=1\]e si scrive \[X_n\operatorname*{\rightarrow}_{P} X\]

Definizione 8.3 (Convergenza in Media Quadratica) Si dice che la successione \(\{X_1,X_2,...,X_n,...\}\) converge in media quadratica alla VC X se e solo se \[\lim_{n\to\infty}E\big((X_n-X)^2\big)=0\]e si scrive \[X_n\operatorname*{\rightarrow}_{L^2} X\]

8.2 Somme e Medie di VC

Siano \(X_1,...,X_n\) \(n\) VC IID, tali che \(E(X_i)=\mu\) e \(V(X_i)=\sigma^2\). Chiamiamo \(S_n\) la somma delle \(X_i\) \[S_n =X_1+...+X_n=\sum_{i=1}^nX_i\] Dalle proprietà del valore atteso e della varianza otteniamo \[\begin{eqnarray*} E(S_n) &=& E(X_1+...+X_n)\\ &=& E(X_1)+...+E(X_n)\\ &=& \mu+...+\mu\\ &=& n\mu\\ V(S_n) &=& V(X_1+...+X_n)\\ &=& V(X_1)+...+V(X_n)\\ &=& \sigma^2+...+\sigma^2\\ &=& n\sigma^2 \end{eqnarray*}\]

Chiamiamo \(\bar X\) la media delle \(X_i\) \[\bar X= \frac{S_n}n =\frac{X_1+...+X_n}n=\frac 1n\sum_{i=1}^nX_i\] Dalle proprietà del valore atteso e della varianza otteniamo \[\begin{eqnarray*} E(\bar X) &=& E\left(\frac{S_n}{n}\right)\\ &=& \frac 1n E(S_n)\\ &=& \mu\\ V\left(\bar X\right) &=& V\left(\frac{S_n}{n}\right)\\ &=& \frac 1{n^2}V(S_n)\\ &=& \frac {\sigma^2}n \end{eqnarray*}\]

Le VC \(X_1,...,X_n\) sono VC qualunque non necessariamente normali, il fatto che chiamiamo \(E(X_i)=\mu\) e \(V(X_i)=\sigma^2\) è solo una convenzione e non deve fare pensare ai parametri della normale.

Teorema 8.1 (Legge dei Grandi Numeri) Siano \(X_1,...,X_n\) \(n\) VC IID, tali che \(E(X_i)=\mu\) e \(V(X_i)=\sigma^2\). Posto \[\bar X= \frac{S_n}n =\frac{X_1+...+X_n}n=\frac 1n\sum_{i=1}^nX_i\] allora \(\bar X\) converge in media quadratica alla VC \(X\) che assume il valore \(\mu\) con probabilità 1.

Dimostrazione. Dalla definizione di convergenza in media quadratica, dobbiamo studiare il limite \[\lim_{n\to\infty}E\big((\bar X-X)^2\big)\] Siccome \(X\) è tale che \(P(X=\mu)=1\) allora \[\lim_{n\to\infty}E\big((\bar X-\mu)^2\big)\] ma essendo \(E\big((\bar X-\mu)^2\big)=V(\bar X)=\sigma^2/n\) otteniamo \[\lim_{n\to\infty}\frac {\sigma^2}n=0\]

Quindi la media di VC converge alla media dell’urna se il numero di VC aumenta all’infinito. Ma mentre converge al punto della media, cosa succede? A questa domanda rispondono i teoremi centrali del limite.

8.3 Teoremi del Limite Centrale

I Teoremi del Limite Centrale (TLC), central limit theorems, sono una famiglia di teoremi sul limite delle somme di VC. Occupano un posto centrale nella teoria della probabilità e dell’inferenza statistica. Esistono molti enunciati a seconda delle ipotesi di partenza. In questo corso mostriamo il teorema più noto e lo decliniamo in tre casi particolari.

I TLC riguardano la convergenza in distribuzione di una successione di somme di una VC. La potenza del teorema è che, non importa quale sia la distribuzione di partenza delle \(X_i\), la loro somma, per \(n\) abbastanza grande, è approssimabile con una distribuzione normale. Enunciamo qui tre diversi teoremi che in realtà sono tre diverse declinazioni dello stesso. Iniziamo dal primo e più famoso.

Teorema 8.2 (TLC per la Somma) Siano \(X_1....,X_n\), \(n\) Variabili Casuali (VC) Indipendenti e Identicamente Distribuite (IID), tali che \(E(X_i)=\mu\), \(V(X_i)=\sigma^2\), \(\forall i=1....,n\). Posto \[S_n=X_1+...+X_n,\] allora \[S_n\operatorname*{\sim}_{a} N\left(n\mu,n\sigma^2\right)\]

Il TLC per la somma asserisce che la somma di VC IID, se il numero di addendi è sufficientemente grande, si può approssimare con una normale semplificando notevolmente il calcolo.

Siccome una media non è altro che una somma diviso \(n\), valore atteso e varianza le abbiamo già ricavate, otteniamo

Teorema 8.3 (TLC per la Media) Siano \(X_1....,X_n\), \(n\) Variabili Casuali (VC) Indipendenti e Identicamente Distribuite (IID), tali che \(E(X_i)=\mu\), \(V(X_i)=\sigma^2\), \(\forall i=1....,n\). Posto \[\bar X =\frac {S_n} n = \frac{X_1+...+X_n}n,\] allora \[\bar X\operatorname*{\sim}_{a} N\left(\mu,\frac{\sigma^2}n\right)\]

Il TLC per la media asserisce che la media di VC IID, se il numero di elementi che la contengono è sufficientemente grande, si può approssimare con una normale semplificando notevolmente il calcolo. La varianza di questa normale \(\sigma^2/n\) va a zero per \(n\) che diverge, e ci riporta alla legge dei grandi numeri.

Se consideriamo le \(X_i\) tutte Bernoulli di parametro \(\pi\) sappiamo che \(E(X_i)=\pi\) e \(V(X_i)=\pi(1-\pi)\). Dedichiamo alla media di Bernoulli un simbolo speciale che sarà più chiaro più avanti. \[\hat \pi=\frac{X_1+...+X_n}{n}\] sostituendo valore atteso e varianza nel TLC della media otteniamo:

Teorema 8.4 (TLC per la Proporzione) Siano \(X_1....,X_n\), \(n\) Variabili Casuali (VC) Indipendenti e Identicamente Distribuite (IID), tali che \(X_i\sim\text{\rm Ber}(\pi)\), \(\forall i=1....,n\). Posto \[\hat\pi =\frac {S_n} n = \frac{X_1+...+X_n}n,\] allora \[\hat\pi\operatorname*{\sim}_{a} N\left(\pi,\frac{\pi(1-\pi)}n\right)\]

Il TLC per la proporzione è sempre il TLC per la media ma per VC di Bernoulli. Ci dice che la proporzione osservata su un campione di \(n\) VC di Bernoulli è normale con media \(\pi\) e varianza che va a zero con \(n\) che diverge.

La notazione \(\operatorname*{\sim}_{a}\) non è una notazione standard ma è diventata una prassi con i miei studenti per semplificare la notazione completa che sarebbe più elaborata. Per esempio nel caso del TLC della somma anziché scrivere \[ S_n\operatorname*{\sim}_{a} N(n\mu,n\sigma^2) \] avremmo dovuto scrivere \[ S_n\operatorname*{\rightarrow}_{d} X,~~~~ X\sim N(n\mu,n\sigma^2) \] che complica troppo la trattazione.

8.3.1 Esempio Somma

Siano \(X_1, X_2,...,X_n\) \(n\) VC IID con supporto \(S_X=\{-1,0,+1\}\) e con funzione di probabilità \[ \begin{cases} P(X=-1)&=\frac 13\\ P(X=\phantom{-}0)&=\frac 13\\ P(X=+1)&=\frac 13 \end{cases} \] Consideriamo \[ S_2=X_1+X_2 \] il supporto di \(S_2\) sarà \[S_{S_2}=\{-2,-1,0,+1,+2 \} \] \(S_2=-2\) se sia \(X_1=-1\) e \(X_2=-1\), \(S_2=-1\) se sia \(X_1+X_2=-1\) ecc. mettiamo in tabella

\[ \begin{array}{ r|rrrrrr } & -1 ;&\color{blue}{ \frac{ 1 } { 3 }} & 0 ;&\color{blue}{ \frac{ 1 } { 3 }} & 1 ;&\color{blue}{ \frac{ 1 } { 3 }} \\ \hline -1 ;\color{blue}{ 1 / 3 }& -2;&\color{red}{\frac{1}{9}}& -1;&\color{red}{\frac{1}{9}}& 0;&\color{red}{\frac{1}{9}}\\ 0 ;\color{blue}{ 1 / 3 }& -1;&\color{red}{\frac{1}{9}}& 0;&\color{red}{\frac{1}{9}}& 1;&\color{red}{\frac{1}{9}}\\ 1 ;\color{blue}{ 1 / 3 }& 0;&\color{red}{\frac{1}{9}}& 1;&\color{red}{\frac{1}{9}}& 2;&\color{red}{\frac{1}{9}}\\ \end{array} \]

E ricaviamo la distribuzione di, S_2

\[ \begin{array}{ r|rrrrr } S_2 & -2& -1& 0& 1& 2 \\ \hline P( S_2 ) & \frac{1}{9}& \frac{2}{9}& \frac{3}{9}& \frac{2}{9}& \frac{1}{9} \\ \end{array} \]

Se siamo interessati ad \(S_3\) \[ S_3=X_1+X_2+X_3=S_2+X_3 \]

lavoriamo come prima facendo la somma tra \(S_2\) e \(X_1\)

\[ \begin{array}{ r|rrrrrr } & -1 ;&\color{blue}{ \frac{ 1 } { 3 }} & 0 ;&\color{blue}{ \frac{ 1 } { 3 }} & 1 ;&\color{blue}{ \frac{ 1 } { 3 }} \\ \hline -2 ;\color{blue}{ 1 / 9 }& -3;&\color{red}{\frac{1}{27}}& -2;&\color{red}{\frac{1}{27}}& -1;&\color{red}{\frac{1}{27}}\\ -1 ;\color{blue}{ 2 / 9 }& -2;&\color{red}{\frac{2}{27}}& -1;&\color{red}{\frac{2}{27}}& 0;&\color{red}{\frac{2}{27}}\\ 0 ;\color{blue}{ 3 / 9 }& -1;&\color{red}{\frac{3}{27}}& 0;&\color{red}{\frac{3}{27}}& 1;&\color{red}{\frac{3}{27}}\\ 1 ;\color{blue}{ 2 / 9 }& 0;&\color{red}{\frac{2}{27}}& 1;&\color{red}{\frac{2}{27}}& 2;&\color{red}{\frac{2}{27}}\\ 2 ;\color{blue}{ 1 / 9 }& 1;&\color{red}{\frac{1}{27}}& 2;&\color{red}{\frac{1}{27}}& 3;&\color{red}{\frac{1}{27}}\\ \end{array} \]

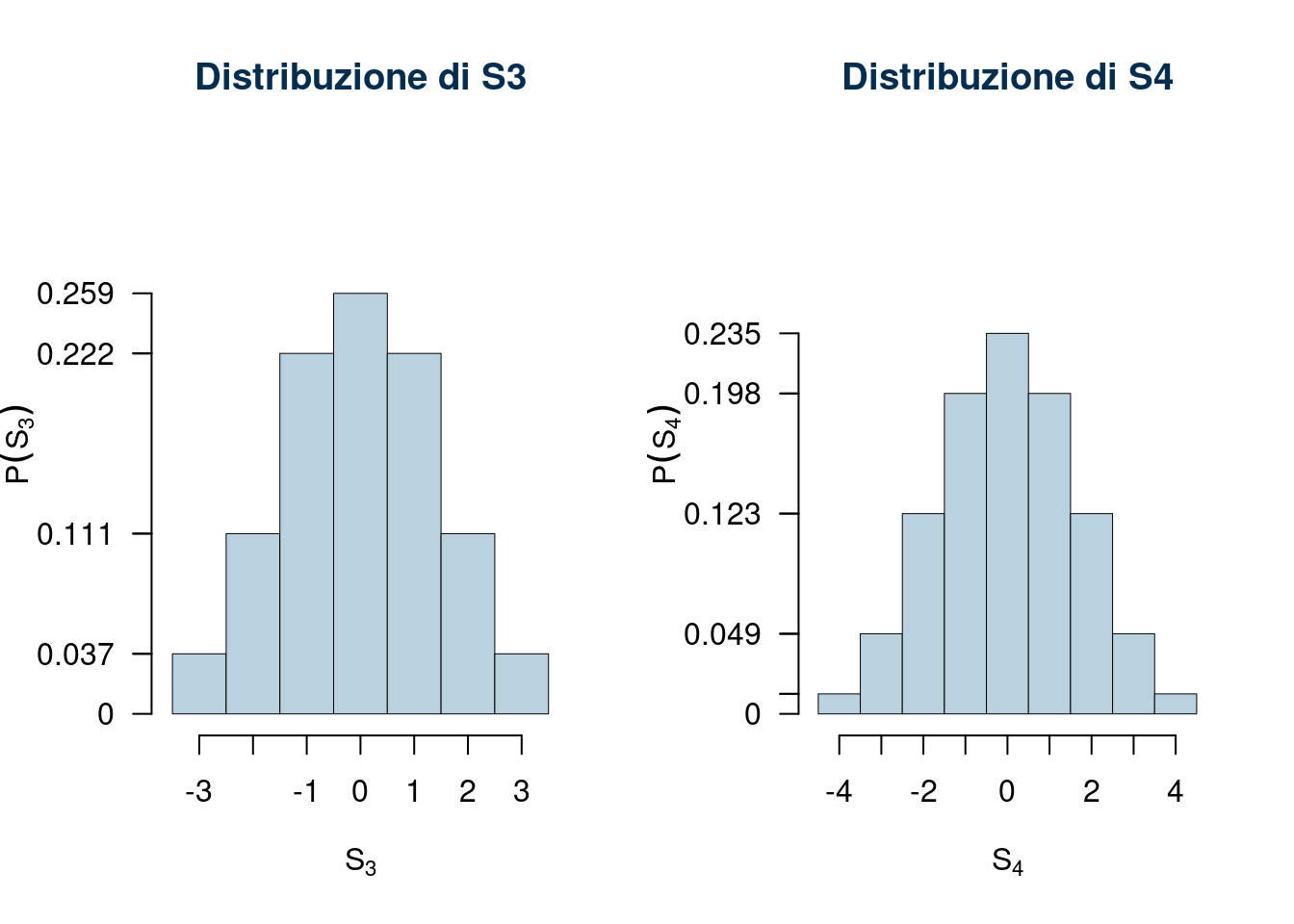
E ricaviamo la distribuzione di, S_3

\[ \begin{array}{ r|rrrrrrr } S_3 & -3& -2& -1& 0& 1& 2& 3 \\ \hline P( S_3 ) & \frac{1}{27}& \frac{3}{27}& \frac{6}{27}& \frac{7}{27}& \frac{6}{27}& \frac{3}{27}& \frac{1}{27} \\ \end{array} \]

Iteriamo il ragionamento per \(S_4\)

\[ S_4=S_3+X_4 \]

\[ \begin{array}{ r|rrrrrr } & -1 ;&\color{blue}{ \frac{ 1 } { 3 }} & 0 ;&\color{blue}{ \frac{ 1 } { 3 }} & 1 ;&\color{blue}{ \frac{ 1 } { 3 }} \\ \hline -3 ;\color{blue}{ 1 / 27 }& -4;&\color{red}{\frac{1}{81}}& -3;&\color{red}{\frac{1}{81}}& -2;&\color{red}{\frac{1}{81}}\\ -2 ;\color{blue}{ 3 / 27 }& -3;&\color{red}{\frac{3}{81}}& -2;&\color{red}{\frac{3}{81}}& -1;&\color{red}{\frac{3}{81}}\\ -1 ;\color{blue}{ 6 / 27 }& -2;&\color{red}{\frac{6}{81}}& -1;&\color{red}{\frac{6}{81}}& 0;&\color{red}{\frac{6}{81}}\\ 0 ;\color{blue}{ 7 / 27 }& -1;&\color{red}{\frac{7}{81}}& 0;&\color{red}{\frac{7}{81}}& 1;&\color{red}{\frac{7}{81}}\\ 1 ;\color{blue}{ 6 / 27 }& 0;&\color{red}{\frac{6}{81}}& 1;&\color{red}{\frac{6}{81}}& 2;&\color{red}{\frac{6}{81}}\\ 2 ;\color{blue}{ 3 / 27 }& 1;&\color{red}{\frac{3}{81}}& 2;&\color{red}{\frac{3}{81}}& 3;&\color{red}{\frac{3}{81}}\\ 3 ;\color{blue}{ 1 / 27 }& 2;&\color{red}{\frac{1}{81}}& 3;&\color{red}{\frac{1}{81}}& 4;&\color{red}{\frac{1}{81}}\\ \end{array} \]

E ricaviamo la distribuzione di, S_4

\[ \begin{array}{ r|rrrrrrrrr } S_4 & -4& -3& -2& -1& 0& 1& 2& 3& 4 \\ \hline P( S_4 ) & \frac{1}{81}& \frac{4}{81}& \frac{10}{81}& \frac{16}{81}& \frac{19}{81}& \frac{16}{81}& \frac{10}{81}& \frac{4}{81}& \frac{1}{81} \\ \end{array} \]

Osserviamo i grafici per \(n=1,...,4\)

Calcolare \(S_n\) se \(n\) è un numero elevato è difficoltoso. Il TLC ci viene incontro. Possiamo calcolare valore atteso e varianza della VC della VC che ha generato il sistema.

\[\begin{eqnarray*} E(X) &=& -1 \frac 13+0\frac 13+1 \frac 13=0\\ V(X) &=& (-1)^2\frac 13 +0^2\frac 13+1^2\frac 13-0^2=\frac 23 \end{eqnarray*}\]

e quindi in virtù del TLC per la somma \[ S_n\operatorname*{\sim}_a N(n\cdot 0, n\cdot 2/3) \] Se per esempio \(n=50\) \[ S_{50}\operatorname*{\sim}_a N(0,50\cdot 2/3) \] e quindi se volessi calcolare la probabilità che \(S_{50}<3\) useremmo la distribuzione normale

\[\begin{eqnarray*} P( S_n < 3 ) &=& P\left( \frac { S_n - \mu }{ V(S_n) } < \frac { 3 - 0 }{\sqrt{ 33.33 }} \right) \\ &=& P\left( Z < 0.52 \right) \\ &=& \Phi( 0.52 ) \\ &=& 0.6985 \end{eqnarray*}\]

8.3.2 Roulette

Il gioco. Una giocata dalla roulette equivale ad estrarre da un’urna che contiene 37 bussolotti numerati da 0 a 36.

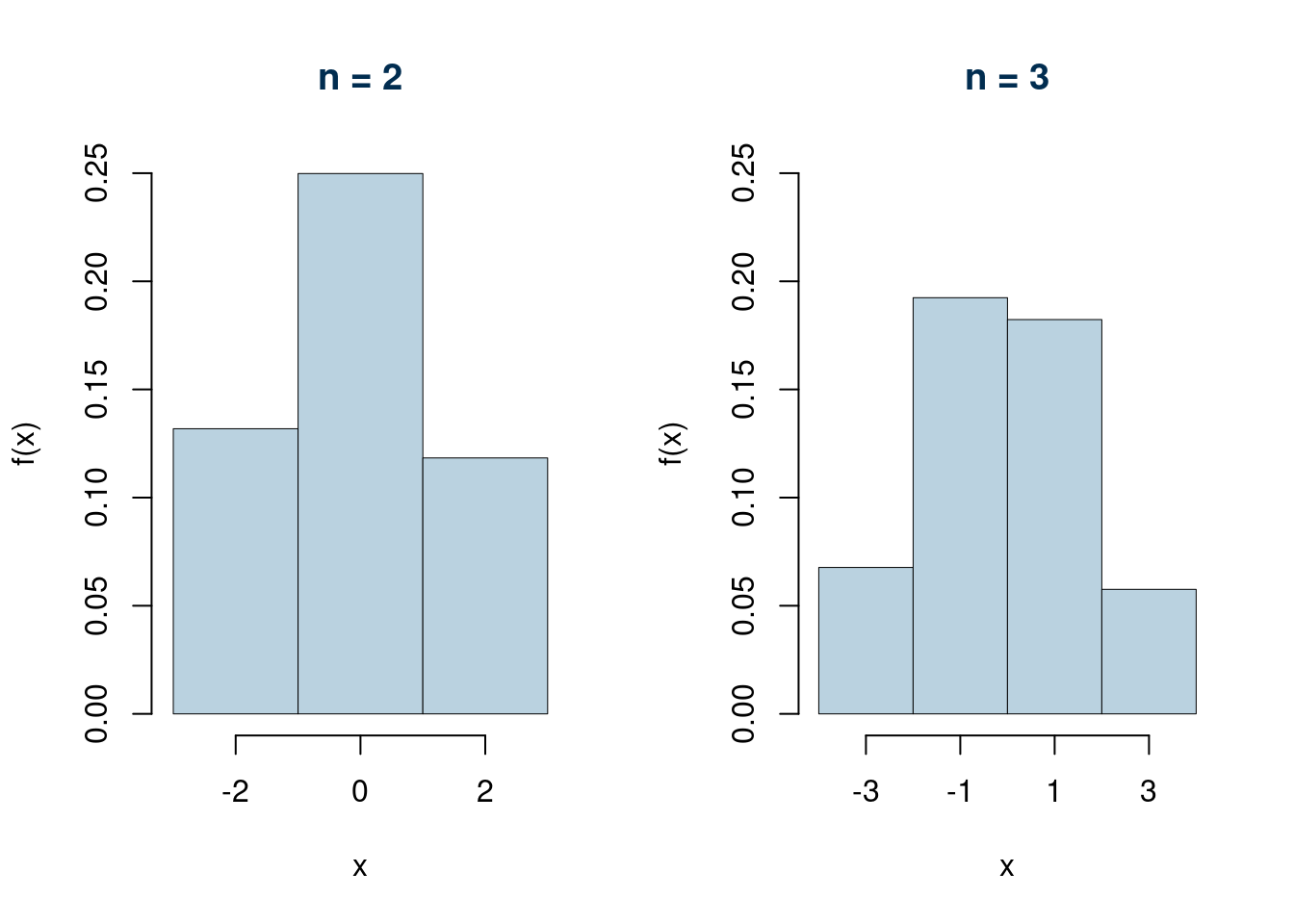
Si può puntare su diverse combinazioni: pari o dispari, rosso o nero, da 1 a 18 o da 19 a 36,… e altre combinazioni. Se puntiamo 1€, per esempio, su Rosso la vincita/perdita sarà: \[ \begin{cases} +1€, &\text{se esce Rosso}\\ -1€, &\text{se non esce Rosso} \end{cases} \] Giocheremo, sempre puntando un euro alla volta, per \(n\) volte. La VC \(R_i\) che descrive l’evento Rosso o non Rosso, nella giocata \(i\), è una Bernoulli di parametro \[ \pi=\frac{18}{37}=0.4865 \] Sia la VC \(X_i\) che descrive la vincita/perdita \[X_i=-1+2R_i\] Se \(R_i=1\) allora \(X_i=-1+2\times 1=+1\), mentre se \(R_i=0\) allora \(X_i=-1+2\times 0=-1\) La VC \(R_i\sim\text{Ber}(\pi=0.4865)\) e quindi \[\begin{eqnarray*} E(R_i) &=& 0.4865\\ V(R_i) &=& 0.4865\times(1-0.4865) \end{eqnarray*}\] E quindi \[\begin{eqnarray*} E(X_i) &=& -1+2\times 0.4865\\ &=&-0.02703\\ V(X_i) &=& 2^2\times 0.4865\times(1-0.4865)\\ &=& 0.9993 \end{eqnarray*}\] Le \(X_i\) sono tutte tra di loro Indipendenti e Identicamente Distribuite (IID). Se quindi giochiamo \(n\) volte la VC che conta il numero di euro vinti/persi è \[ S_n = X_1+...+X_n \] Riscrivendo in termini di \(R_i\) \[\begin{eqnarray*} S_n &=& -1 + 2R_1 -1 + 2R_2 +...+(-1)+2R_n\\ &=& -n + 2(R_1+...+R_n)\\ &=& -n + 2R \end{eqnarray*}\] \(R=R_1+...+R_n\sim \text{Bin}(n;\pi=0.4865)\) Se per esempio gioco due (\(n=2\)) volte \[ S_2 = X_1+X_2 \] il supporto di \(S_2\) è l’insieme \(\{-2,0,+2\}\). \[\begin{eqnarray*} P(S_2=-2)&=&P(R_1+R_2=0)= \binom{2}{0}0.4865^0(1-0.4865)^2=0.2637\\ P(S_2=0)&=&P(R_1+R_2=1)= \binom{2}{1}0.4865^1(1-0.4865)^1=0.4996\\ P(S_2=+2)&=&P(R_1+R_2=2)= \binom{2}{0}0.4865^2(1-0.4865)^0=0.2367 \end{eqnarray*}\]

Se per esempio gioco tre (\(n=3\)) volte \[ S_2 = X_1+X_2+X_3=S_2+X_3 \] il supporto di \(S_3\) è l’insieme \(\{-3,-1,+1,+3\}\). \[\begin{eqnarray*} P(S_3=-3)&=&P(R_1+R_2+R_3=0)= \binom{3}{0}0.4865^0(1-0.4865)^3=0.1354\\ P(S_3=-1)&=&P(R_1+R_2+R_3=1)= \binom{3}{1}0.4865^1(1-0.4865)^2=0.3849\\ P(S_3=+1)&=&P(R_1+R_2+R_3=2)= \binom{3}{2}0.4865^2(1-0.4865)^1=0.3646\\ P(S_3=+3)&=&P(R_1+R_2+R_3=3)= \binom{3}{3}0.4865^3(1-0.4865)^0=0.1151 \end{eqnarray*}\]

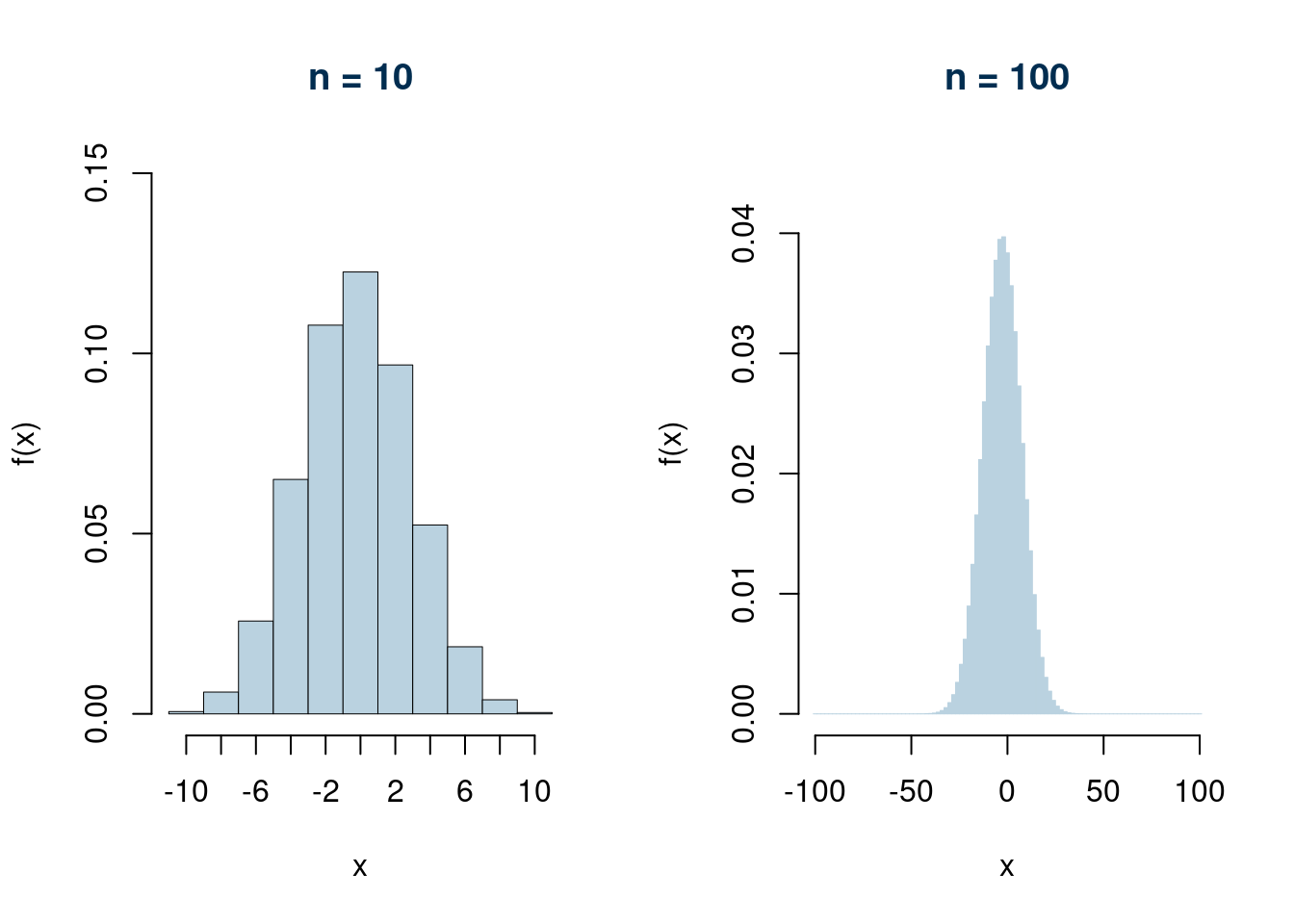
Se per esempio gioco tre (\(n=10\)) volte \[ S_{10} = S_9+X_{10} \]

Se per esempio gioco tre (\(n=100\)) volte \[ S_{100} = S_{99}+X_{100} \] La probabilità di non perdere è data da.

\[\begin{eqnarray*} P(S_{100}>0)&=& P(-100+2R>0)\\ &=& P(R>100/2)\\ &=&P(R>50)\\ &=&P(R=51)+P(R=52)+...+P(R=100)\\ &=&\binom{100}{51}0.4865^{51}(1-0.4865)^{49}+\binom{100}{52}0.4865^{52}(1-0.4865)^{48}+...\\ &+& \binom{100}{100}0.4865^{100}(1-0.4865)^{0}\\ &=& 0.3553 \end{eqnarray*}\]

Approssimazione normale

\[\begin{eqnarray*} \mu &=& E(X_i)\\ &=& -1+2\times 0.4865\\ &=&-0.02703\\ \sigma^2 &=& V(X_i) \\ &=& 2^2\times 0.4865\times(1-0.4865)\\ &=& 0.9993 \end{eqnarray*}\]

posto \[ S_n = X_1+...+X_n \] e dunque

\[\begin{eqnarray*} E(S_n) &=& E(X_1+...+X_n)\\ &=& E(X_1)+...+E(X_n)\\ &=& \mu+...+\mu\\ &=& n\mu\\ &=& -2.7027\\ V(S_n) &=& V(X_1+...+X_n)\\ &=& V(X_1)+...+V(X_n)\\ &=&\sigma^2+...+\sigma^2\\ &=& n\sigma^2\\ &=& n\times 0.9993 \end{eqnarray*}\]

Per \(n=100\)

\[\begin{eqnarray*} E(S_n) &=& 100\times (-0.02703)\\ &=& -2.7027\\ V(S_n) &=& 100\times 0.9993\\ &=& 99.927 \end{eqnarray*}\]

In virtù del teorema del limite centrale

\[\begin{eqnarray*} S_{100}&&\operatorname*{\sim}_{a} N(100\times(-0.02703),100\times0.9993)\\ && \operatorname*{\sim}_{a} N(-2.7027,99.927) \end{eqnarray*}\]

E quindi

\[\begin{eqnarray*} P( S_n > 0 ) &=& P\left( \frac { S_n - E(S_n) }{ \sqrt{V(S_n)} } > \frac { 0 - ( -2.7027 ) }{\sqrt{ 99.93 }} \right) \\ &=& P\left( Z > 0.27 \right) \\ &=& 1-P(Z< 0.27 )\\ &=& 1-\Phi( 0.27 ) \\ &=& 0.3936 \end{eqnarray*}\]

I due valori di probabilità esatta 0.3553 e quello approssimato 0.3934 sono diversi nella seconda cifra decimale. Questo è dovuto al fatto che la normale calcola anche parte dell’istogramma della binomiale in zero. Per ovviare e migliorare l’approssimazione basta spostare sulla fine del rettangolo dello zero il calcolo della normale. Senza entrare nel dettaglio si ricava che il rettangolo finisce per \(S_n=1\) e dunque

\[\begin{eqnarray*} P( S_n > 1 ) &=& P\left( \frac { S_n - E(S_n) }{ \sqrt{V(S_n)} } > \frac { 1 - ( -2.7027 ) }{\sqrt{ 99.93 }} \right) \\ &=& P\left( Z > 0.37 \right) \\ &=& 1-P(Z< 0.37 )\\ &=& 1-\Phi( 0.37 ) \\ &=& 0.3557 \end{eqnarray*}\]