Capitolo 9 Statistiche campionarie
9.1 Risultati preliminari
Consideriamo \(n\) variabili casuali, \(X_1,...,X_n\), IID, con valore atteso e varianza, rispettivamente, \(\mu\) e \(\sigma^2\). Sono dati che stiamo per osservare e quindi sono casuali.
Definizione 9.1 Una statistica campionaria, \(S\), è una funzione dei dati \(X_1,...,X_n\) \[S(X_1,...,X_n)=s\in\mathbb{R}\]
Come funzione di VC \(S=S(X_1,...,X_n)\) è una VC. Ad esempio la media dei dati è una statistica, il 25-esimo percentile è una statistica, la mediana dei dati, la varianza, ecc. Ci possiamo porre alcune domande, per esmepio:
- come si distribuisce una media campionaria di valori casuali? \[\hat \mu=\bar X \operatorname*{\sim}_a N\left(\mu,\frac{\sigma^2}n\right)\] dove, \(E(\hat\mu)=\mu\), \(V(\hat\mu)=\frac{\sigma^2}n\)
- Come si distribuisce la varianza campionaria di valori casuali? \[\hat\sigma^2=\frac 1 n \sum_{i=1}^n (X_i-\hat \mu)^2 \sim ?\]
9.2 La distribuzione Chi-quadro \(\chi^2\)
Definizione 9.2 Siano \(Z_1,...,Z_n\), \(n\) VC, IID, \(Z_i\sim N(0,1)\), posto, \[Y=Z_1^2+...+Z_n^2, \qquad \text{allora} \qquad Y\sim \chi^2_n\] La distribuzione della somma del quadrato di \(n\) normali standard è distribuita come un chi-quadro con \(n\) gradi di libertà
La VC ha come supporto tutta la retta reale positiva: \[S_Y=\{y>0\}=\mathbb{R}^+\] Lo spazio dei parametri non ha interesse statistico \[n\in\mathbb{Z}^+\]
Funzione di probabilista o densità: \[ f(x)=\dfrac {x^{{\frac {n}{2}}-1}e^{-{\frac {x}{2}}}}{2^{\frac {n}{2}}\Gamma \left({\frac {n}{2}}\right)} \] dove \[ \Gamma(t)=\int_0^{+\infty}x^{t-1}e^{-x}dx \]
- per \(n = 1\) ha una forma iperbolica;
- per \(n>2\) e a forma campanulare con un’asimmetria positiva (coda lunga a dx);
- in virtù del TLC se \(n\) diverge allora \(Y\stackrel{\sim}{a}N(n,2n)\). \[E(Y)=n,\qquad V(Y)=2n\]
In figura 9.1 e 9.1 la forma della densità al variare di \(n\).
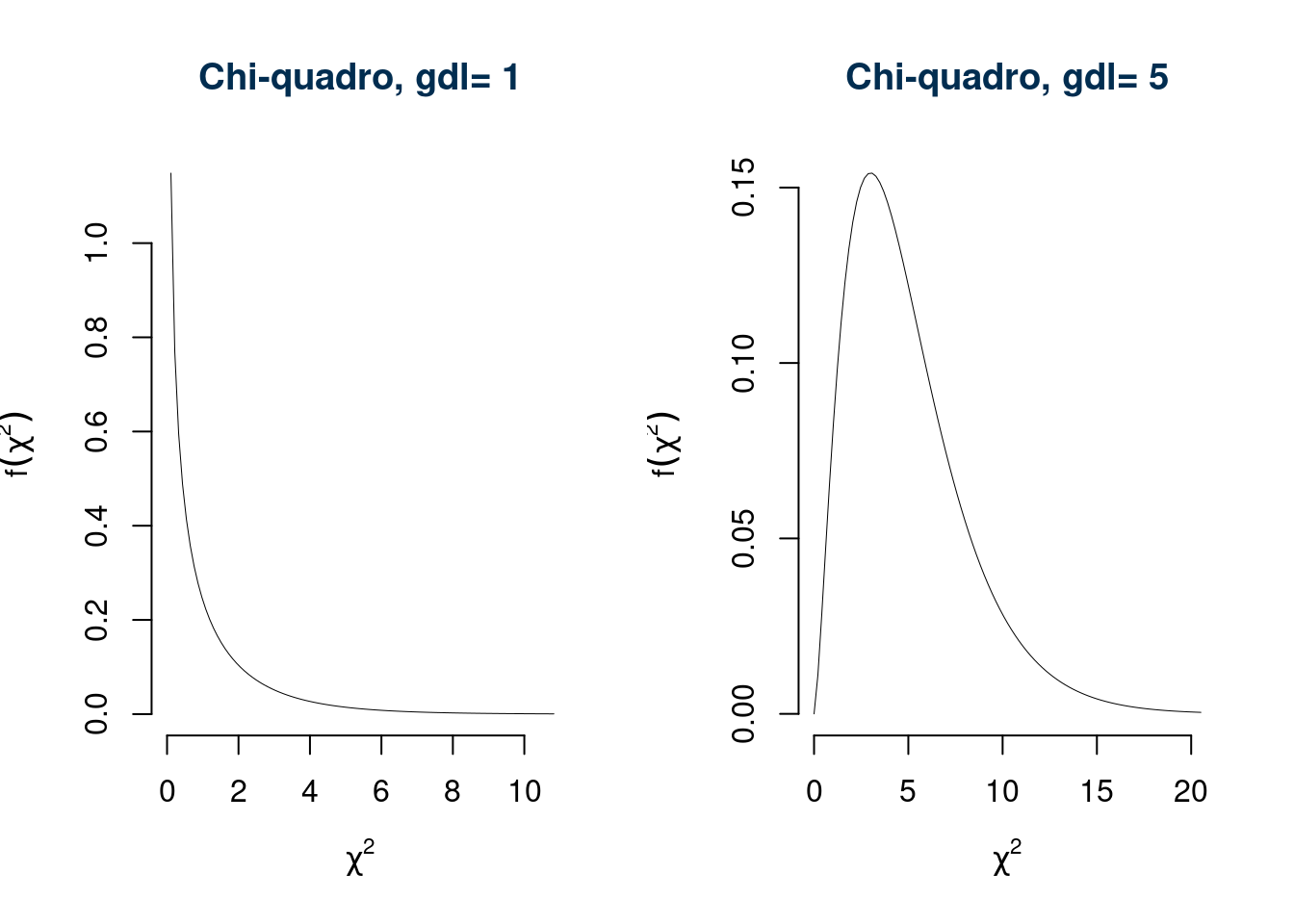
Figura 9.1 La densità della VC Chi-quadro per diversi valori di \(n\)
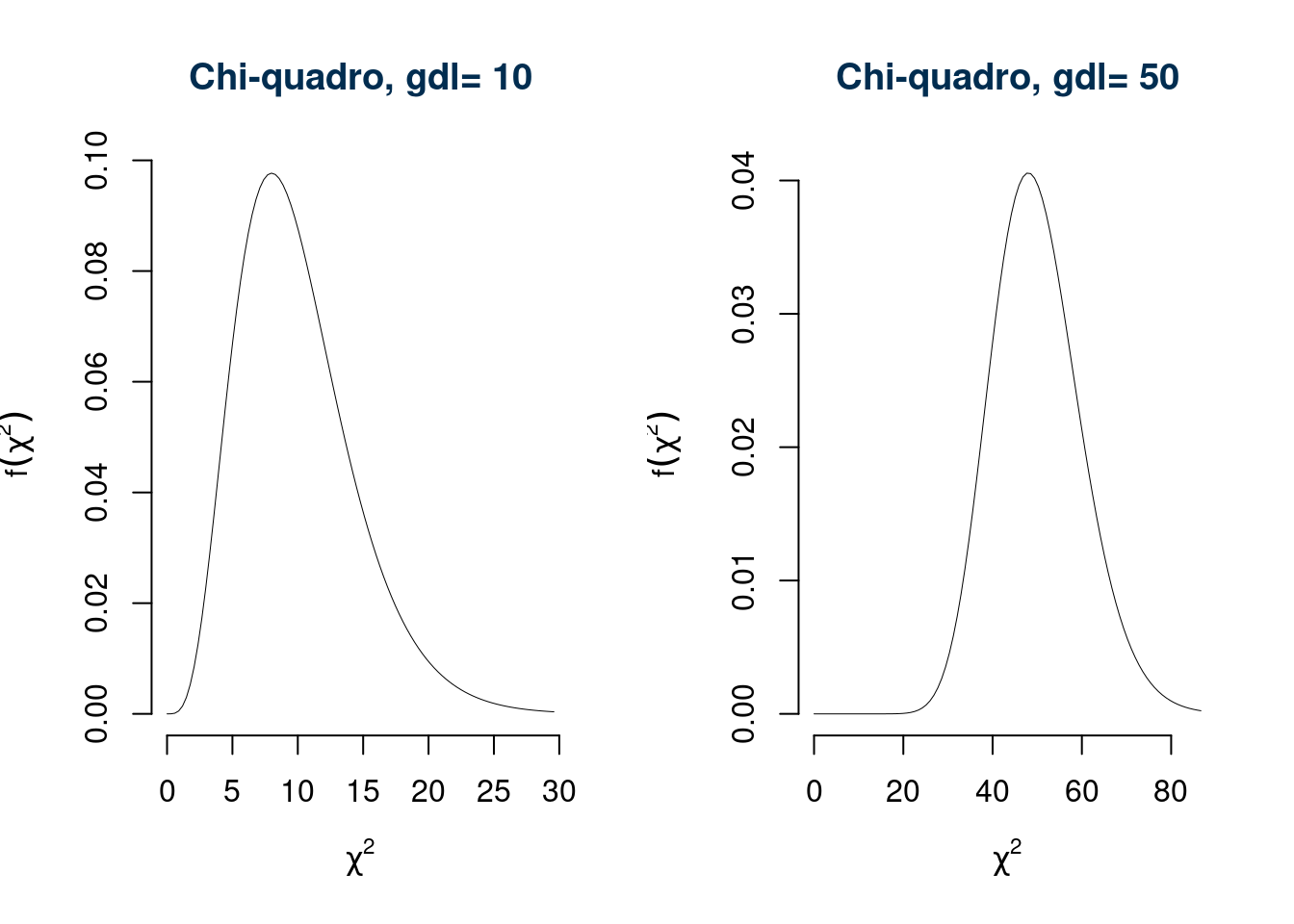
Figura 9.2 La densità della VC Chi-quadro per diversi valori di \(n\)
9.2.1 Le tavole del \(\chi^2\)
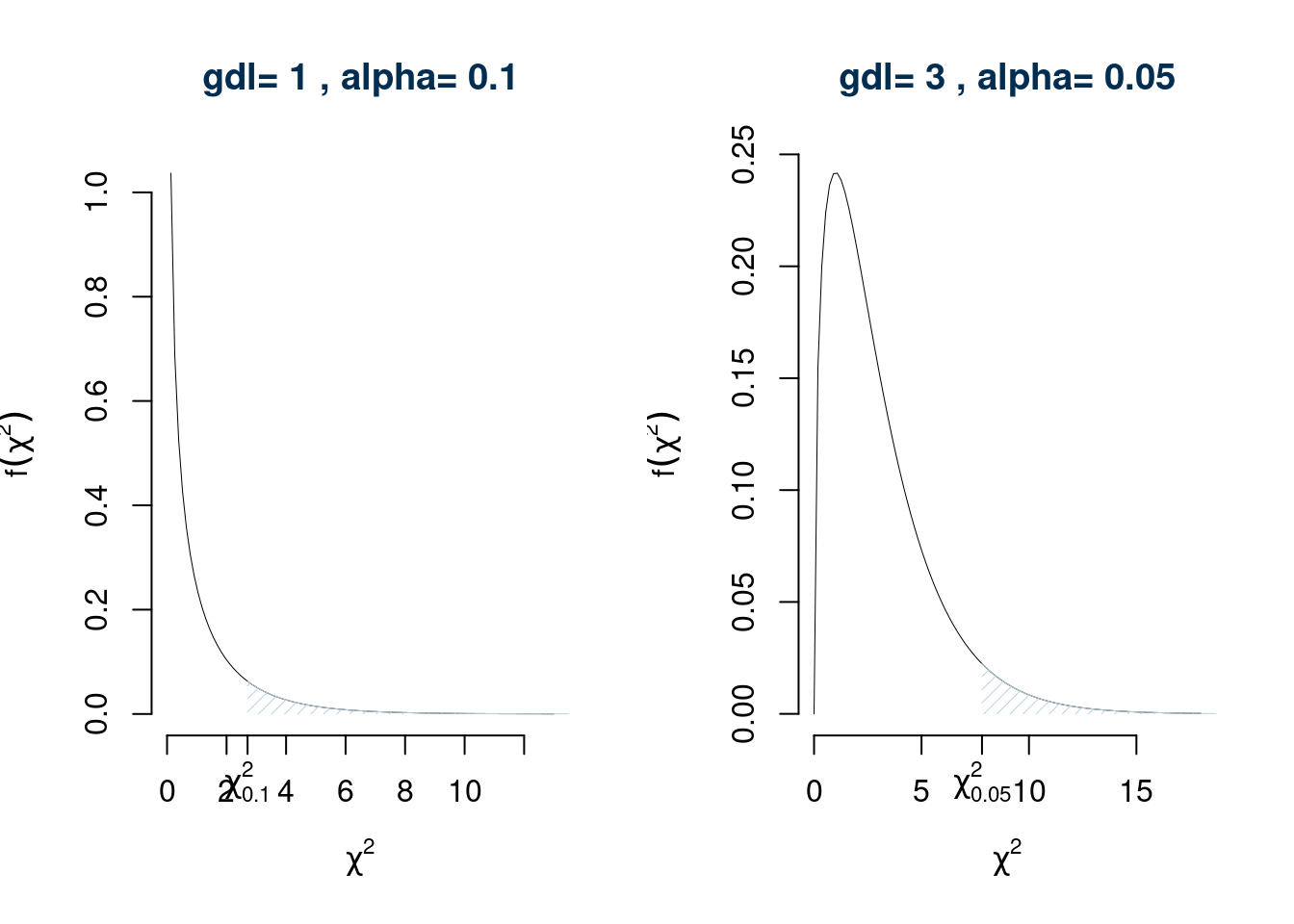
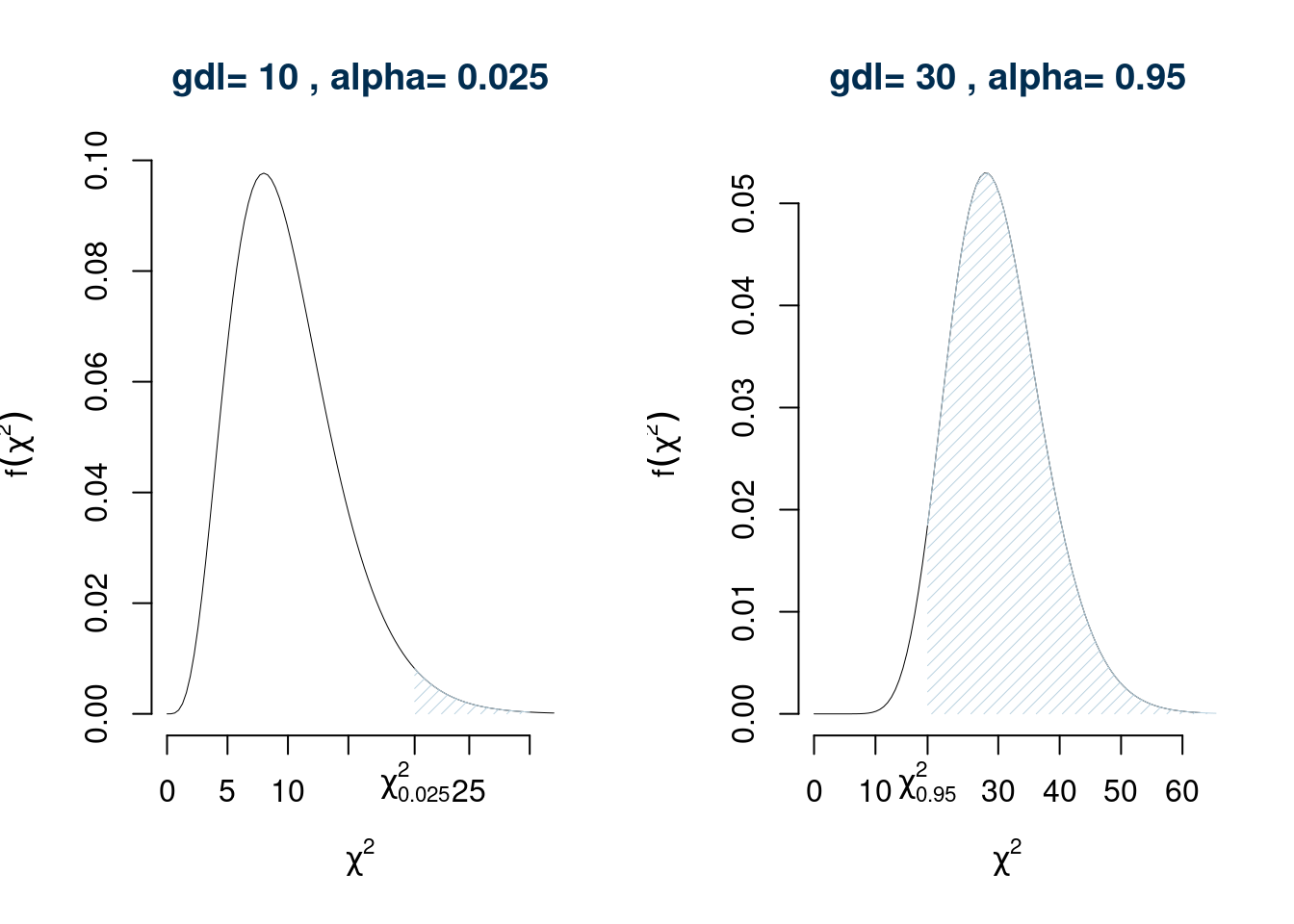
Non c’è una sola distribuzione \(\chi^2\) ma tante quante sono i possibili gradi di libertà. Per comodità editoriale vengono mostrati solo alcuni valori delle code, per alcuni gradi di libertà. Offrono il percentile della \(\chi^2\) per diversi gradi di libertà e diversi valori di \(\alpha\), ovvero \[P(\chi^2_n>\chi^2_{n;\alpha})=\alpha\] per alcuni valori di \(n\) e di \(\alpha\). Le tavole si presentano in forma tabellare dove ogni riga è indicizzata dal grado di libertà e ogni colonna dal valore di probabilità \(\alpha\).
| GdL | \(\alpha=\) 0.99950 | \(\alpha=\) 0.99900 | \(\alpha=\) 0.99500 | \(\alpha=\) 0.99000 | \(\alpha=\) 0.97500 | \(\alpha=\) 0.95000 | \(\alpha=\) 0.90000 |
|---|---|---|---|---|---|---|---|
| 1 | 0.00000 | 0.00000 | 0.00004 | 0.00016 | 0.00098 | 0.00393 | 0.01579 |
| 2 | 0.00100 | 0.00200 | 0.01003 | 0.02010 | 0.05064 | 0.10259 | 0.21072 |
| 3 | 0.01528 | 0.02430 | 0.07172 | 0.11483 | 0.21580 | 0.35185 | 0.58437 |
| 4 | 0.06392 | 0.09080 | 0.20699 | 0.29711 | 0.48442 | 0.71072 | 1.06362 |
| 5 | 0.15814 | 0.21021 | 0.41174 | 0.55430 | 0.83121 | 1.14548 | 1.61031 |
| 6 | 0.29941 | 0.38107 | 0.67573 | 0.87209 | 1.23734 | 1.63538 | 2.20413 |
| 7 | 0.48487 | 0.59849 | 0.98926 | 1.23904 | 1.68987 | 2.16735 | 2.83311 |
| 8 | 0.71038 | 0.85710 | 1.34441 | 1.64650 | 2.17973 | 2.73264 | 3.48954 |
| GdL | \(\alpha=\) 0.10000 | \(\alpha=\) 0.05000 | \(\alpha=\) 0.02500 | \(\alpha=\) 0.01000 | \(\alpha=\) 0.00500 | \(\alpha=\) 0.00100 | \(\alpha=\) 0.00050 |
|---|---|---|---|---|---|---|---|
| 1 | 2.70554 | 3.84146 | 5.02389 | 6.63490 | 7.87944 | 10.82757 | 12.11567 |
| 2 | 4.60517 | 5.99146 | 7.37776 | 9.21034 | 10.59663 | 13.81551 | 15.20180 |
| 3 | 6.25139 | 7.81473 | 9.34840 | 11.34487 | 12.83816 | 16.26624 | 17.73000 |
| 4 | 7.77944 | 9.48773 | 11.14329 | 13.27670 | 14.86026 | 18.46683 | 19.99735 |
| 5 | 9.23636 | 11.07050 | 12.83250 | 15.08627 | 16.74960 | 20.51501 | 22.10533 |
| 6 | 10.64464 | 12.59159 | 14.44938 | 16.81189 | 18.54758 | 22.45774 | 24.10280 |
| 7 | 12.01704 | 14.06714 | 16.01276 | 18.47531 | 20.27774 | 24.32189 | 26.01777 |
| 8 | 13.36157 | 15.50731 | 17.53455 | 20.09024 | 21.95495 | 26.12448 | 27.86805 |
Quindi per esempio se sono interessato a sapere quale valore del \(\chi_3^2\) lascia alla sua destra lo 0.05 dell’area dovrò cercare sulla terza riga in corrispondenza della colonna 0.05 e quindi \[ \chi_{3;0.05}^2=7.8147 \]
9.3 La distribuzione \(t\)-di Student
Definizione 9.3 Siano \(Z\sim N(0,1)\) e \(Y\sim\chi^2_n\), \(Z\) e \(Y\) indipendenti, posto, \[T=\frac Z{\sqrt{Y/n}} \qquad \text{allora} \qquad T\sim t_n\] Il rapporto tra una normale standard e un la radice di un chi-quadro diviso per i suoi gradi di libertà è distribuito come una \(t\)-Student con \(n\) gradi di libertà
La VC ha come supporto tutta la retta reale: \[S_T=\mathbb{R}\] Lo spazio dei parametri non ha interesse statistico \[n\in\mathbb{Z}^+\]
Funzione di probabilista o densità.
- è a forma campanulare
- è simmetrica rispetto a zero
- all’aumentare di \(n\) le code si abbassano
- Se \(n\to\infty\), allora \(t_n\to N(0,1)\)
\[E(Y)=0,\qquad V(Y)=\frac{n}{n-2}\]
In figura 9.3 e 9.4 il confronto tra la \(t\)-di Student e la normale standard, per diversi valori di \(n\).
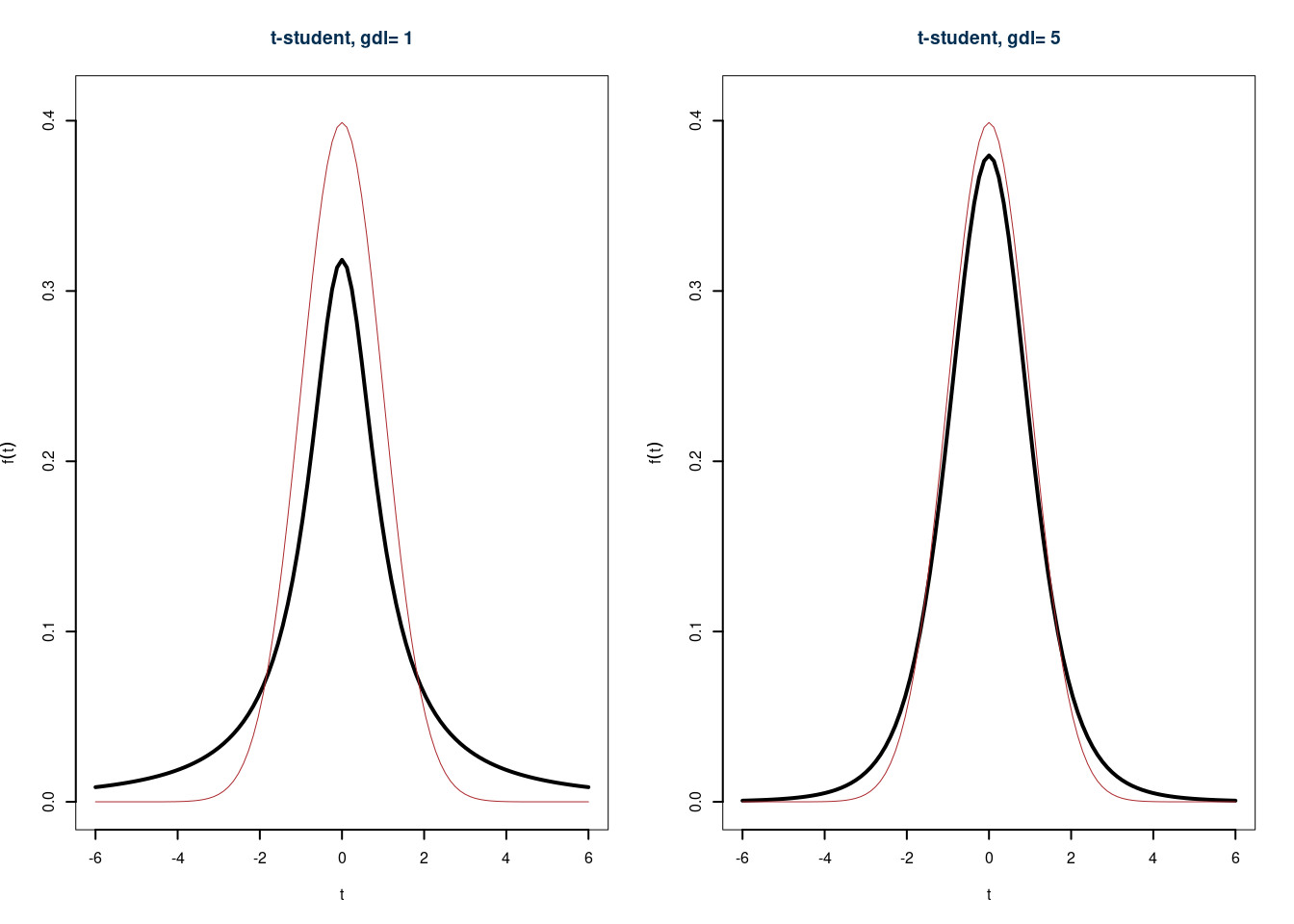
Figura 9.3 confronto tra la \(t\)-di student e la normale standard, per diversi valori di \(n\)
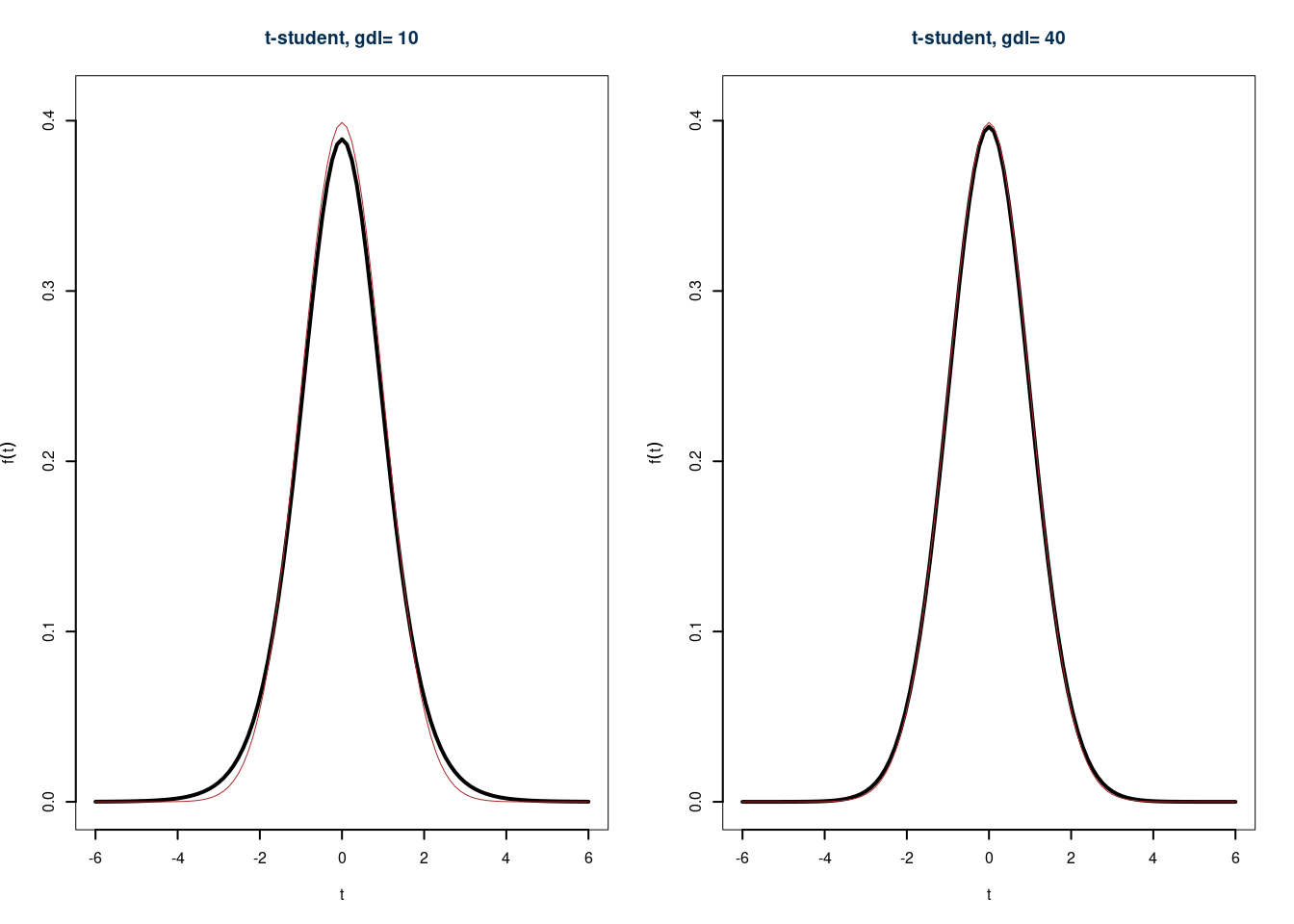
Figura 9.4 confronto tra la \(t\)-di student e la normale standard, per diversi valori di \(n\)
9.3.1 Le tavole della \(t\)
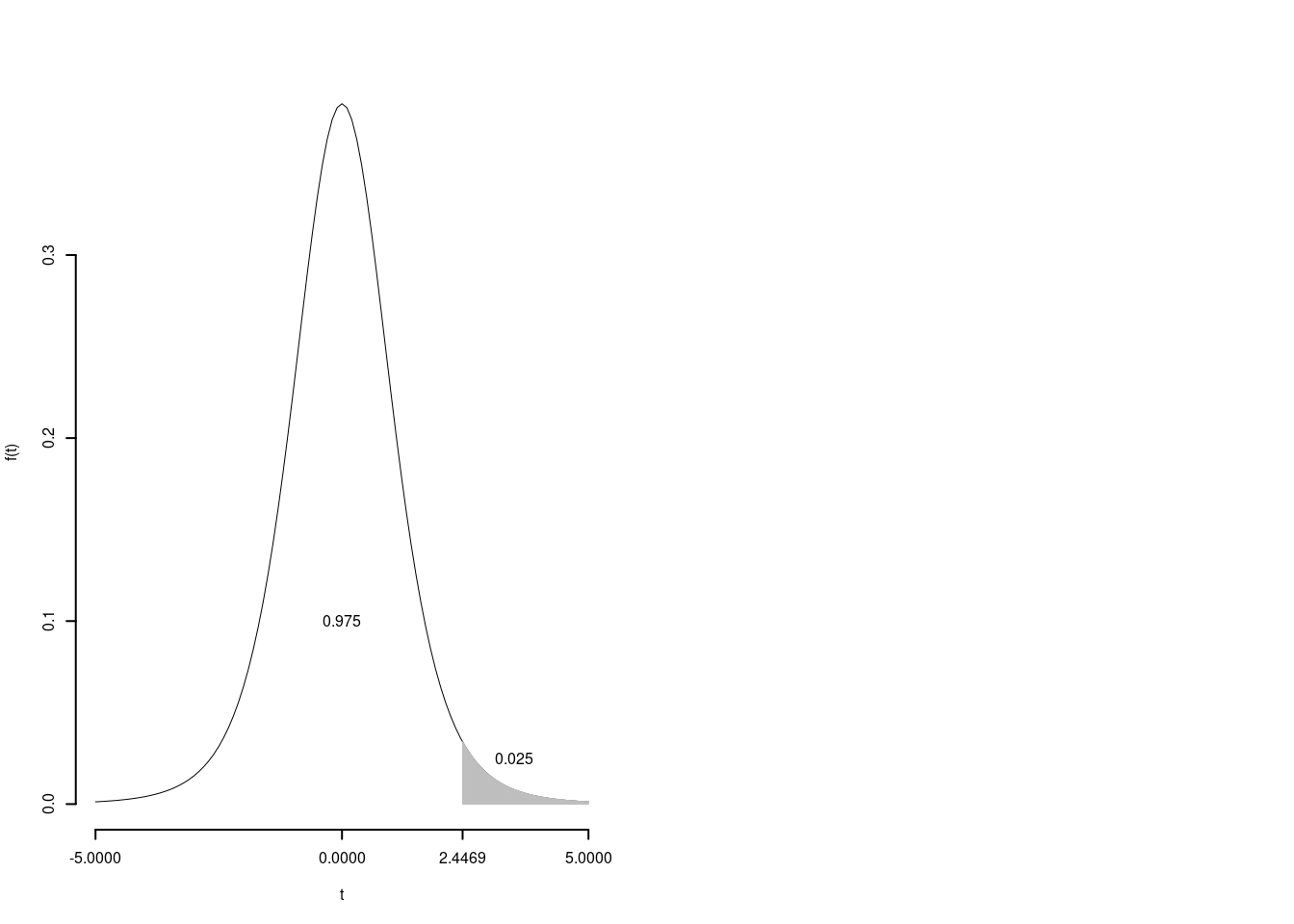
Non c’è una sola distribuzione \(t\) ma tante quante sono i possibili gradi di libertà. Per comodità editoriale vengono mostrati solo alcuni valori delle code, per alcuni gradi di libertà. Sulle tavole leggiamo: \[ P(T>t_{n;\alpha})=\alpha \] per alcuni valori di \(n\) e di \(\alpha\). Le tavole si presentano in forma tabellare dove ogni riga è indicizzata dal grado di libertà e ogni colonna dal valore di probabilità \(\alpha\). Per conoscere quale valore \(t_{6;0.025}\) della \(t_6\) con 6 gradi di libertà, tale che \[ P(T>t_{6;0.025})=0.025 \]
| GdL | \(\alpha=0.1\) | \(\alpha=0.05\) | \(\alpha=0.025\) | \(\alpha=0.01\) | \(\alpha=0.005\) | \(\alpha=0.001\) | \(\alpha=0.0005\) |
|---|---|---|---|---|---|---|---|
| 1 | 3.0777 | 6.3138 | 12.7062 | 31.8205 | 63.6567 | 318.3088 | 636.6192 |
| 2 | 1.8856 | 2.9200 | 4.3027 | 6.9646 | 9.9248 | 22.3271 | 31.5991 |
| 3 | 1.6377 | 2.3534 | 3.1824 | 4.5407 | 5.8409 | 10.2145 | 12.9240 |
| 4 | 1.5332 | 2.1318 | 2.7764 | 3.7469 | 4.6041 | 7.1732 | 8.6103 |
| 5 | 1.4759 | 2.0150 | 2.5706 | 3.3649 | 4.0321 | 5.8934 | 6.8688 |
| 6 | 1.4398 | 1.9432 | 2.4469 | 3.1427 | 3.7074 | 5.2076 | 5.9588 |
| 7 | 1.4149 | 1.8946 | 2.3646 | 2.9980 | 3.4995 | 4.7853 | 5.4079 |
| 8 | 1.3968 | 1.8595 | 2.3060 | 2.8965 | 3.3554 | 4.5008 | 5.0413 |
| 9 | 1.3830 | 1.8331 | 2.2622 | 2.8214 | 3.2498 | 4.2968 | 4.7809 |
| 10 | 1.3722 | 1.8125 | 2.2281 | 2.7638 | 3.1693 | 4.1437 | 4.5869 |
| … | … | … | … | … | … | … | … |
Dunque \(t_{6;0.025}=2.44691\)
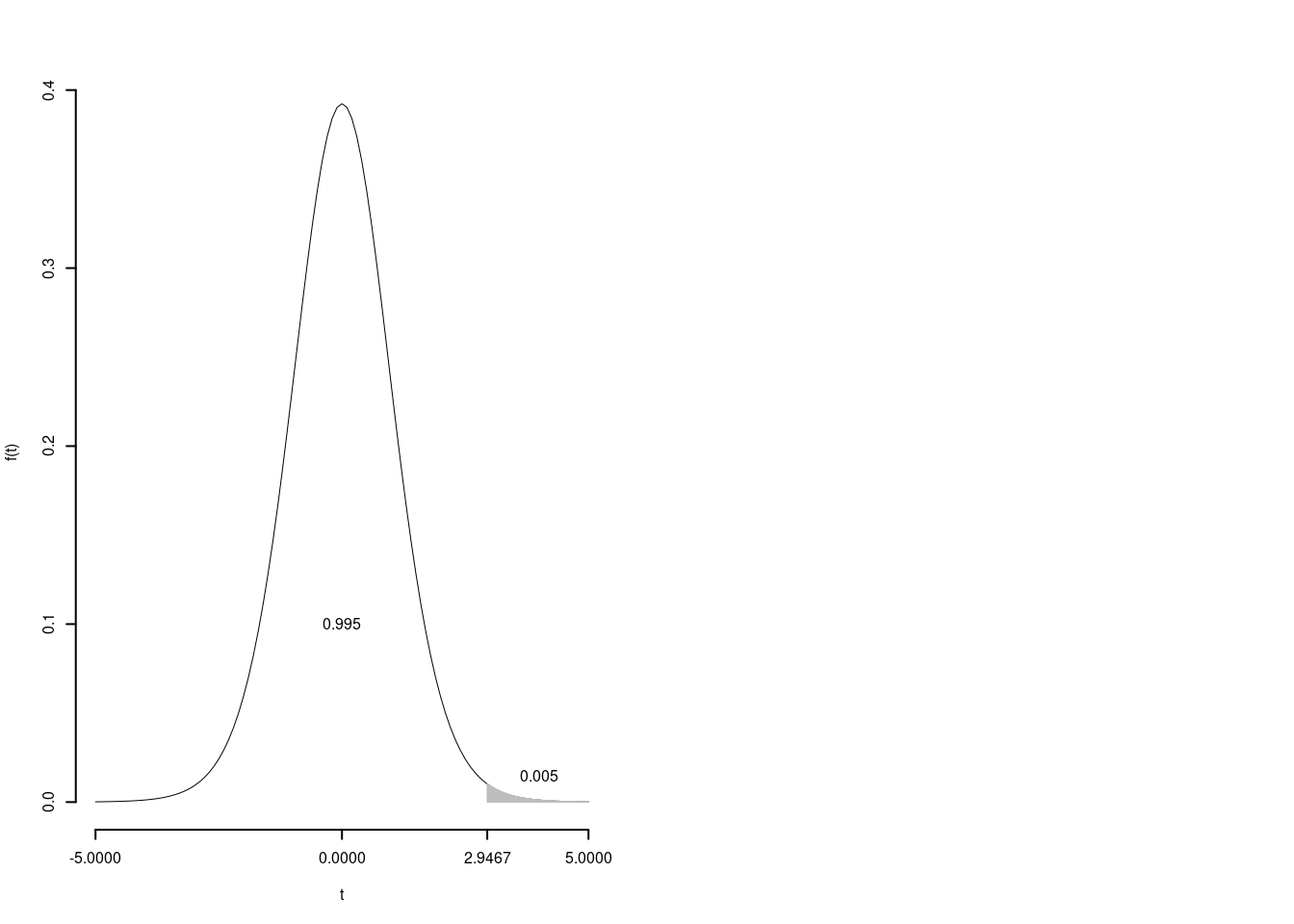
Per conoscere quale valore \(t_{15;0.005}\) della \(t_{15}\) con 15 gradi di libertà, tale che \[P(T>t_{15;0.005})=0.005\]
Dunque \(t_{15;0.005}=2.94671\)
| GdL | \(\alpha=0.1\) | \(\alpha=0.05\) | \(\alpha=0.025\) | \(\alpha=0.01\) | \(\alpha=0.005\) | \(\alpha=0.001\) | \(\alpha=0.0005\) |
|---|---|---|---|---|---|---|---|
| … | … | … | … | … | … | … | … |
| 13 | 1.3502 | 1.7709 | 2.1604 | 2.6503 | 3.0123 | 3.8520 | 4.2208 |
| 14 | 1.3450 | 1.7613 | 2.1448 | 2.6245 | 2.9768 | 3.7874 | 4.1405 |
| 15 | 1.3406 | 1.7531 | 2.1314 | 2.6025 | 2.9467 | 3.7328 | 4.0728 |
| 16 | 1.3368 | 1.7459 | 2.1199 | 2.5835 | 2.9208 | 3.6862 | 4.0150 |
| 17 | 1.3334 | 1.7396 | 2.1098 | 2.5669 | 2.8982 | 3.6458 | 3.9651 |
| … | … | … | … | … | … | … | … |
Per conoscere quale valore \(t_{49;0.0005}\) della \(t_{49}\) con 49 gradi di libertà, tale che \[P(T>t_{49;0.001})=0.001\]
| GdL | \(\alpha=0.1\) | \(\alpha=0.05\) | \(\alpha=0.025\) | \(\alpha=0.01\) | \(\alpha=0.005\) | \(\alpha=0.001\) | \(\alpha=0.0005\) |
|---|---|---|---|---|---|---|---|
| … | … | … | … | … | … | … | … |
| 46 | 1.3002 | 1.6787 | 2.0129 | 2.4102 | 2.6870 | 3.2771 | 3.5150 |
| 47 | 1.2998 | 1.6779 | 2.0117 | 2.4083 | 2.6846 | 3.2729 | 3.5099 |
| 48 | 1.2994 | 1.6772 | 2.0106 | 2.4066 | 2.6822 | 3.2689 | 3.5051 |
| 49 | 1.2991 | 1.6766 | 2.0096 | 2.4049 | 2.6800 | 3.2651 | 3.5004 |
| 50 | 1.2987 | 1.6759 | 2.0086 | 2.4033 | 2.6778 | 3.2614 | 3.4960 |
| … | … | … | … | … | … | … | … |
Dunque \(t_{49;0.001}=3.2651\)
L’ultima riga della \(t\), per un numero infinito di GdL, coincide con la tabella aggiuntiva della \(Z\). Infatti
| GdL | \(\alpha=0.1\) | \(\alpha=0.05\) | \(\alpha=0.025\) | \(\alpha=0.01\) | \(\alpha=0.005\) | \(\alpha=0.001\) | \(\alpha=0.0005\) |
|---|---|---|---|---|---|---|---|
| 80 | 1.2922 | 1.6641 | 1.9901 | 2.3739 | 2.6387 | 3.1953 | 3.4163 |
| 90 | 1.2910 | 1.6620 | 1.9867 | 2.3685 | 2.6316 | 3.1833 | 3.4019 |
| 100 | 1.2901 | 1.6602 | 1.9840 | 2.3642 | 2.6259 | 3.1737 | 3.3905 |
| \(\infty\) | 1.2816 | 1.6449 | 1.9600 | 2.3263 | 2.5758 | 3.0902 | 3.2905 |
La tabella dei percentili della normale è
\[\begin{array}{lrrrrrrr} \hline \alpha & 0.1 & 0.05 & 0.025 & 0.01 & 0.005 & 0.001 & 0.0005 \\ z_\alpha & \color{red}{ 1.2816} &\color{red}{1.6449} &\color{red}{1.9600} &\color{red}{2.3263} &\color{red}{2.5758} &\color{red}{3.0902} &\color{red}{3.2905 } \\ \Phi(z_\alpha)=1-\alpha & 0.9 & 0.95 & 0.975 & 0.99 & 0.995 & 0.999 & 0.9995 \\ \hline \end{array}\]
9.4 La distribuzione di \(\hat\sigma^2\)
Siano \(X_1,...,X_n\), \(n\) VC IID, replicazioni della stessa \(X\sim N(\mu,\sigma^2)\). La si definisce la varianza campionaria
\[\hat\sigma^2=\frac 1 n \sum_{i=1}^n(X_i-\hat \mu)^2, \qquad \hat \mu=\bar X=\frac 1 n \sum_{i=1}^nX_i\]
allora
\[ \hat\sigma^2\sim\frac{\sigma^2}n\chi^2_{n-1}.\]
Osserviamo:
\[\begin{eqnarray*} E(\hat\sigma^2) &=& \frac {\sigma^2}n E(\chi^2_{n-1})\\ &=& \frac{n-1}n \sigma^2 \end{eqnarray*}\]